Measuring and constructing angles with a protractor

Angles of any given size may be drawn, or the size of any angle may be measured, by using an instrument called a pro­tractor (Fig. 13).

A protractor is a semicircular plate graduated from one extremity of the diameter to the other and used to measure angles. The inside numbers show angles in degrees beginning at 0° and going counterclockwise. The outside numbers mark angles in degrees from 0° going clockwise.

Notice that the upper part of the protractor is half a circle. It contains 180 parts. The centre of the semicircle or protractor ,is at point 0. Notice that there are two sets of

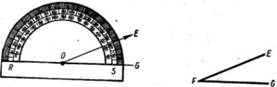
Fig. 13 Fig. 14

numbers on the curved edge so arranged that one set of numbers begins at the right side of the Protractor and the other begins at the left side. This arrangement permits us to measure angles that open at the left or the right sides.

Problem: Find the number of degrees in angle EFG (Fig. 14)
Method: Place the centre of the protractor at point F so the Point 0 of the protractor is on point F and the zero division line at S on the protractor lies on side FG of the angle. Now read the scale where lines Fe crosses the protractor. Reading from the zero at the right we find that angle EFG contains 30°.

If you were to use¹ the outside scale which starts at zero on the left side of the protractor, the reading would be 150°. Since a 150° - angle would be obtuse, and EFG is acute, you would not have the correct measurement for the angle.

Note:

¹ if you were to use — если бы вы использовали

EXERCISES

I.Read the following words paying attention to the pronunciation:

inside, size, side, acute, obtuse, measuring, constructing, arranging, angle, edge, arrange, circle, semicircle.

II.Make up sentences of your own using the words and expressions given below:

if you were to use, is used to measure, may be drawn, protractor, counterclockwise, permits us to measure, to calculate.

III. Answer the following questions:

1 What is a protractor used for? 2. What do inside numbers on the scale of a protractor show? 3. How many parts does the upper part of the protractor contain? 4. What permits us to measure angles that open at the left or at the right side?

IV.Translate into English:

Для измерения углов употребляется специальный прибор- транспортир. Этот прибор представляет собой полукруг, дуга которого разделена на 180 частей. Чтобы измерить угол, накладывают транспортир так, чтобы Центр транспортира совпал с вершиной угла, а радиус был расположен на одной стороне угла. Тогда число градусов, содержащихся Луге заключенной между сторонами угла, покажет нужную величину. При помощи транспортира можно также начертить угол, содержащий данное число градусов.

TEXT

KINDS OF POLYGONS

Triangles. A triangle is a plane figure bounded by three straight lines and containing three angles. The sum of the angles of every triangle is 180°.

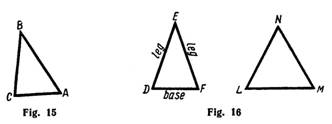
A triangle is identified by naming its vertices in any order. Thus, the triangle given in the figure 15 may be called ∆АВС, ∆BAC, ∆ВСA, ∆САВ, ∆CBA or ∆AСВ. The symbol ∆ means triangle.

Fig. 16 shows the various types of triangles. A scalene triangle (Fig. 15) is a triangle with no two sides equal. An isosceles triangle is a triangle which has two equal sides. The equal sides are called the legs; the third side is called the base. The angles at the base are called the base angles. The angle formed by the two equal sides, is called the vertex angle. An equilateral triangle is a triangle with all three sides equal.

Quadrilaterals. A quadrilateral is a plane figure bounded by four straight lines. There are several kinds of quadrilat­erals (Fig. 17).

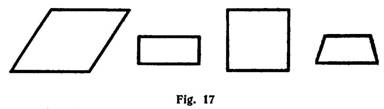
A parallelogram is any quadrilateral in which two pairs of opposite sides are parallel.

A rectangle is a parallelogram whose angles are all right angles.

A square is a rectangle in which all the sides are equal in length.

A trapezoid is a quadrilateral in which only one pair of opposite sides are parallel.

The rectangle and the square both have four right angles. You have learned how to draw a 90º-angle with a protractor and construct the angle with" compasses. Using this knowl­edge, you can construct rectangles and squares.

Other Plane Figures (Fig. 18). A pentagon is a polygon which has five sides. A hexagon is a polygon which has six sides. An octagon is a polygon which has eight sides. A deca­gon is a polygon, which has six sides.

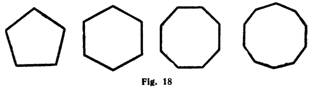Since a regular polygon has equal sides and equal angles, all the vertices are equidistant from the centre.

A circle is a curved line a11 points of which are equidistant from the centre. Therefore, If we inscribe a regular polygon inside of a circle every vertex of the polygon will rest on the line of the circle.

Perimeter. The perimeter of a plane figure is the line around it. The perimeter of each the figures we have been studying would equal the sum of the lengths of its sides.

The perimeter of g rectangle equals two times the length plus two times the width

p = 2l + 2w or p = 2(l + w).

Since a square is a rectangle having four equal sides, we can represent each of the sides by the letter s. The perimeter of the square is expressed by the formula

p = s + s + s + s,

which is written as: p=4s.

The perimeter of a square equals the length of one side mul­tiplied by 4.

EXERCISES

I.Read the following words paying attention to the pronun­ciation:

vertices, isosceles, inscribe, describe, equal, curve, square, rectangle, quadrilaterals, right, parallel, trapezoid, hexagon, octagon, decagon.

II.Underline the prefixes and state their meanings:

polygons, hemisphere, transport, triangle, extraordinary, discharge, semicircle, equilateral, subway, international, coexistence, unequal.

III.Make up sentences of your own using the words and ex­pressions given below:

two times the, length, two times the width, bounded by, to inscribe, equidistant.

IV.Answer the following questions:

1. What is a polygon? 2. What triangles do you know? 3. What kind of quadrilaterals do you know? 4. What is a plane figure? 5. What is the perimeter of a plane figure?

V.Translate into Russian:

The name of the triangle is derived from the Latin word "triangulum"=three-angle, which in its turn was derived from the Greek word "tri-gonon" or three-angle.

Cut a square of convenient size from a sheet of paper. Make a fold from one corner to the opposite corner. Into what kind of triangles is the square divided by the fold in the pa­per?

VI.Translate into English:

Треугольник — это плоская фигура, ограниченная тре­мя линиями и содержащая три угла.

Треугольники бывают равносторонние, разносторон­ние, равнобедренные.

Четырехугольники — это тоже плоские фигуры. Если стороны четырехугольника равны и все углы прямые, то такой четырехугольник называется квадратом.

Многоугольники — это также плоские фигуры. Пяти­угольник имеет пять сторон, шестиугольник — шесть, восьмиугольник — восемь, десятиугольник — десять сто­рон.

Линия вокруг плоской фигуры называется перимет­ром. Периметр плоской фигуры равен сумме длин его сто­рон.

TEXT

CIRCLES

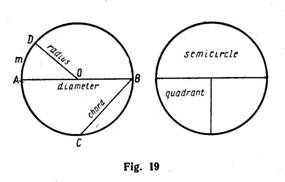A circle is a plane figure bounded by the curved line all points of which are the same distance away from the fixed point, called the centre. The length of the curved line, or the distance around the circle, is its-circumference. A straight line drawn from the centre to any point on the circumference is called a radius (plural: radii). OD the radios (see Fig. 19). The straight line that passes through the centre of the circle and both of whose ends are on the circumference is called a diameter. AB is the diameter. A line segment that connects any two points on the circumference of a circle is a chord. An example is BC.

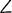Any part of curved line which makes the circle is an arc. The portion of the circle confined in AOD is a sector of the circle, for two sides are radii and the third side is an arc. Because its vertex is at the centre, angle AOD is a central angle.

When a circle is cut in half, each of the halves is called a semi­circle. When a circle is cut into four equal parts, each of the quarters is called a quadrant.

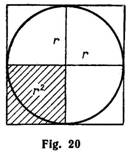
Area of a Circle. If a circle is divided into 4 quadrants and a square is circumscribed about the circle, four small squares are formed (Fig. 20). The side of each small square equal to the radius r. The area of each small square is r²; the area of the large square is equal to the sum of the four small squares, or 4r².

We can see that the area of the circle is about ¾ of the large square. It is approximately equal to 3 ¹/₇ of the small squares, or 3 ¹/₇ r². This can be also written πr².

Rule to remember: the area of a circle equals π, times the radius squared

A= πr².

EXERCISES

I. Read the following words paying attention to the pronun­ciation:

circle, curved, approximately, fixed, called, connects, circumference, arc, cut, check, centre, side, square.

II. Make up sentences of your own using the words and expres­sions given below:

circumference, to pass through, both of whose ends, con­fine in, cut in half.

III. Answer the following questions:

1. What kind of geometrical figure is the circle? 2. What is a radius? 3. What is a diameter? 4. What is a circumfer­ence? 5. How is a half of the circle called? 6. To what is the area of a circle equal?

IV. Translate into Russian:

A circle is generally designated in writing and printing by means of the symbol and a letter indicating the point which is its centre. If it is necessary to describe the circle in more detail, the radius or diameter is also stated, or at least three points through which it passes are named.

A sector equal to a fourth part or quarter of a circle is called a quadrant.

V. Translate into English:

Отрезок прямой, соединяющей две какие-либо точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром. Диаметр равен сумме двух радиусов, и потому все диаметры одной окруж­ности равны между собой. Любая часть окружности назы­вается дугой.

TEXT

GEOMETRIC SOLIDS

We have been studying plane figures, which have only two dimensions: length and width. Now we shall study figures with three dimensions. Figures that have three dimensions are called geometric solids or solid figures. The three dimen­sions of solid figures are length, width, and or height.

Prisms. A prism is a solid, each side of which is a polygon, and the upper base of which is parallel and congruent (exactly the same in size and shape), to the lower base: corresponding vertices of the top and bottom polygons are joined by parallel edges (Fig. 21). In a right prism, the lateral

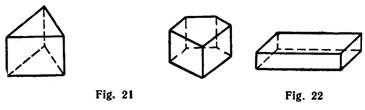
faces (sides) are perpendicular to the bases. Right prisms include: the rectangular prism and the cube. A geometric figure which has six sides, all of which are rectangles, is called a rectangular solid or rectangular prism (Fig. 22). If the dimensions (length, width and height) of a rectangular solid are, the solid is called a cube. The faces of a cube are squares (Fig. 23).

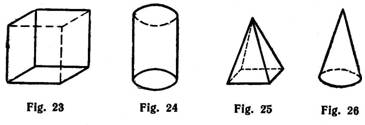
The Right Circular Cylinder. A cylinder (Fig. 24) is a circular prism, the bases of which are equal circles that are parallel to each other. If the sides of the cylinder are perpendicular to the bases, the cylinder is called a right cylinder. The axis of a right circular cylinder is the line between the centres of the bases.

A pyramid (Fig. 25) is a solid figure formed by a polygon called the base and sides of triangles meeting at a common point called the vertex.

A cone is much like a pyramid but has a circle for a base (Fig. 26).

EXERCISES

I.Read the following words paying attention to the pronuncia­tion:

cylinder, prism, figure, width, which, bottom, cone, scalene, between.

II. Give the singular of the words:

phenomena, radii, bases, data.

III. Make up sentences of your own using the words and ex­pressions given below:

to meet at a common point, perpendicular to the bases, equal, parallel to, formed by.

IV. Answer the following questions:

1. What geometric figures have three dimensions? 2. What are the dimensions of solid figures? 3. What geometric solids do you know? 4. What cylinder is called a right cylinder? 5. What is a pyramid?

V. Translate into Russian:

A curved, surface, it will be remembered, is a surface of which no portion is plane. As curved lines may have any cur­vature or shape, so also may a curved surface. A curved sur­face may be of indefinite extent, or it may be a closed sur­face; and a closed surface may have fixed, definite edges or boundaries or it may not.

VI.Translate into English:

Плоские геометрические фигуры имеют два измерения: ширину и длину. Стереометрия изучает геометрические фи­гуры, которые имеют три измерения: длину, ширину и высоту. Призма — это пространственная фигура, каждая грань которой является многоугольником. Если длина, ширина и высота параллелепипеда равны, то такой парал­лелепипед называется кубом. Пирамидой называется мно­гогранник, одной из граней которого служит многоуголь­ник, а остальные грани (боковые) — треугольники с об­щей вершиной.

TEXT

SYMMETRY

Line Symmetry. A dotted line has been drawn in this figure (Fig. 27). The figure is now divided into two parts that have the same size and shape. If the figure is folded on the dotted line, the two parts will coincide. We say that the figure is symmetrical about the dotted line. The dotted line is called the axis of symmetry.

It is possibly for a figure to have more than one axis of symmetry. In Fig. 27 line RS is an axis of symmetry. If we fold the figure along RS, the two parts will coincide. A point

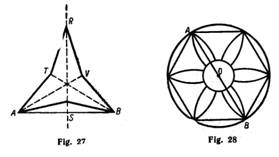
on the left side will fall on only one point on the right side. Any two such points are called corresponding points. For example, A and B are corresponding points. AV is also an axis of symmetry. Then B and R are corresponding points. What is the third possible axis of symmetry? What two points will correspond when this axis is drawn?

Notice, if line AB is drawn, the axis of symmetry RS is perpendicular to, and bisects AB. If a figure has line symmetry, then the axis of symmetry must be perpendicular to the line joining every two corresponding points and must also bisect it.

Point Symmetry. If a dotted line is drawn from any one point on the figure above to any corresponding point, the dotted line will be bisected in the point 0. The figure has balance about point 0 and is therefore, an example of point symmetry. Point 0 is called the centre of symmetry (Fig. 28).

If a figure has point symmetry, then the line which con­nects every two corresponding points must pass through the centre of symmetry and be bisected by it.

It is possible for a figure to have both point symmetry and line symmetry. An example is the circle. Any diameter will be an axis of symmetry. Hence the circle possesses line symmetry.

Pick any point A on a circle. Connect this point with cen­tre 0. Extend this line to a point B, on the other side of the circle. The radius OA is equal to the radius OB. Because this is true of any line drawn through 0 and bounded at either end by the circle, 0 is the centre of symmetry and the circle possesses point symmetry as well as line symmetry.

Plane Symmetry. If a solid can be divided into two equal solids by a plane, and if every part on one side of the plane has a corresponding part on the other, the original solid has plane symmetry.

EXERCISES

I. Read the following word, paying attention to the pronun­ciation:

dotted, folded, corresponding, point, coincide, side, pos­sible, impossible, bisect.

II. Form participles using the following verbs:

to coincide, to draw, to call, to join, to correspond, to divide, to fold.

III. Make up sentences of your own using the words and ex­pressions given below:

to fold on the dotted line, to be symmetrical about the dotted line, to fold the figure along, to fold on the left side.

IV. Answer the following questions:

1.What figure has a line symmetry? 2. How many axes of symmetry can figures have? 3. What points are called cor­responding ones? 4. What is meant by point symmetry? 5. What is meant by plane symmetry?

TEXT

SIMILAR FIOURES

Seeonthe Fig 29. The two figures look alike but one is a smaller copy of the other. These are similar figures: figures having the same shape but not necessary the same size.

The sides in the same position are the corresponding sides of the figures, and the angles in the same position are the corresponding angles of the figures. For example, A'B'(read A prime B prime) are corresponding sides in the figures above, and ABD and A'B'D' are corresponding angles. The corresponding angles of similar polygons are equal.

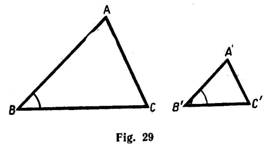
If the ratio of side AB to side A'B' is 2:1, then the ratio of a pair of any other two corresponding sides must also be 2:1. The corresponding sides of similar polygons will be parallel if the polygons are placed in the same position.

Rule to Remember: Two polygons are similar if two conditions are satisfied:

1) corresponding sides are proportional;

2) responding angles are equal.

EXERCISES

I. Read the following words paying attention to the pronunciation:

dimension, condition, slide, alike, line, similar, equal, , that, those, this, they.

II.Make up sentences of your own using the words and expressions given below:

to look alike, in the same position, but not necessarily, corresponding sides.

III.Answer the following questions:

1. What figures do we call similar ones? 2. What angles of similar polygons are equal? 3. When are two polygons similar?

IV.Translate into Russian:

Whenever you draw a map or a plan to scale, you draw a figure similar to the original in shape but different in size. When we reduce the size of a photograph, the smaller picture is similar to the larger one.

In similar triangles the ratio of any pair of corresponding sides equals the ratio of either of the other pairs; that is, they are proportional. In similar triangles the corresponding angles are equal.

TRIGONOMETRY

TEXT