Локальная и интегральная формулы Муавра - Лапласа
Если число испытаний достаточно велико, а произведение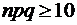 
, то вероятность 
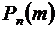находится по локальной формуле Муавра – Лапласа:
,
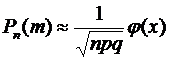где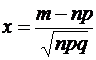 
, а значения функции 
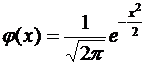приведены в прил. П. 1.
Функция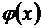 
обладает следующими свойствами:
а) является четной, то есть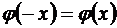 
;
б) 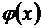монотонно убывает при положительных значениях аргумента;
в)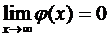 
;
г) для всех значений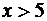 
значение функции 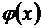= 0.
Вероятность того, что частота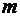 
наступления события 
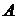попадет в промежуток 
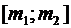при тех же условиях ( , 
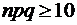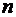достаточно велико) находится приближенно по интегральной формуле Муавра – Лапласа
,
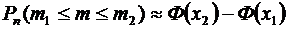где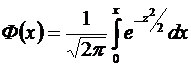 
– функция Лапласа,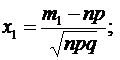 
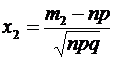(таблица функции 
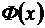приведена в прил. П. 2 данного пособия).
Функция 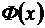обладает следующими свойствами:
а) является нечетной, то есть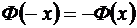 
;
б) 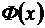- монотонно возрастающая;
в)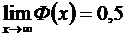 
;
г) для всех значений 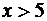значение функции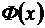 
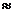0,5.
Рассмотрим следствие интегральной формулы Муавра – Лапласа.
Следствие. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе 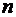независимых испытаний вероятность того, что:
а) число 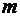наступлений события 
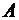отличается от произведения 
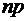не более чем на величину 
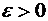(по абсолютной величине), равна
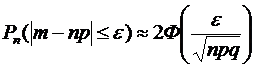; (2)
б) частота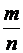 
появлений события 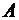в 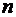испытаниях отличается от постоянной вероятности р не более, чем на число 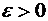(по абсолютной величине), равна
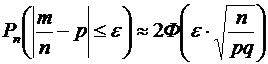. (3)
Данное следствие позволяет решать задачи, в которых по двум из трех величин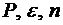 
можно определить третью.
Примеры.
1.Вероятность появления события А в каждом из 625 испытаний равна 0,64. Найти вероятность того, что событие А в этих испытаниях появится ровно 415 раз.
Решение.По условию,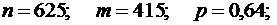 
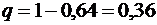. Так как
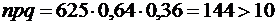,то воспользуемся формулой: 
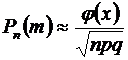, где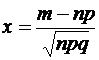 
. Имеем 
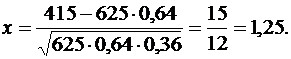По таблице значений функции 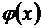находим, что 
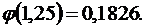Подставляя это значение в формулу, получим: 
.
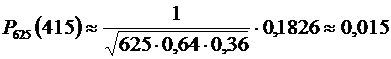Ответ: 0,015.
2.Вероятность попадания в цель при отдельном выстреле равна 0,6. Найти вероятность того, что число попаданий при 600 выстрелах будет заключено в пределах от 330 до 375.
Решение.По условию имеем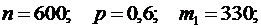 
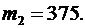Так как
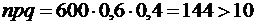,воспользуемся формулой:
,
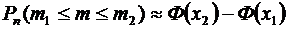где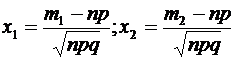 
.
Находим х1 и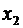 
: 
, 
.
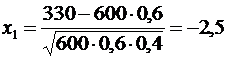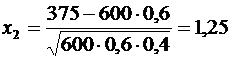По таблице значений функции 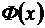, имеем:
.
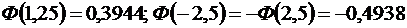Подставив эти значения в формулу, получим:
.
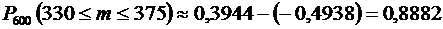Ответ: 0,8882.
3.В каждом из 700 независимых испытаний событие А происходит с постоянной вероятностью 0,35. Найти вероятность того, что событие А происходит: а) меньше чем 270 и больше, чем 230 раз; б) больше, чем 270 раз.
Решение: а) необходимо найти
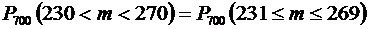. Воспользуемся формулой 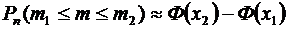, где 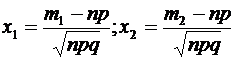. По условию, имеем:
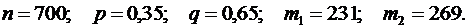Находим х1 и : 
, 
.
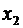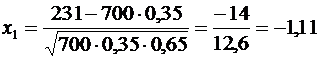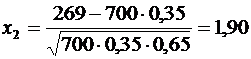По таблице значений функции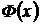 
, имеем:
.
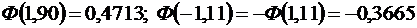Подставив эти значения в формулу, получим:
;
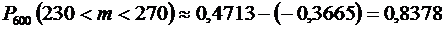б) здесь необходимо найти:
.
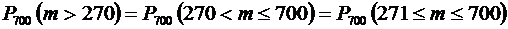Воспользуемся той же формулой, что и в пункте а). По условию, имеем: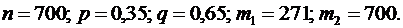 
Находим х1 и : 
, 
.
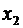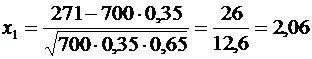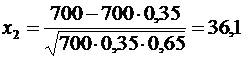По таблице значений функции 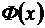, имеем:
.
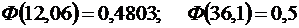Подставив эти значения в формулу, получим:
.
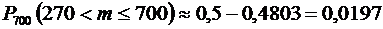Ответ: а) 0,8378; б) 0,0197.
4.В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.
Решение. Имеем: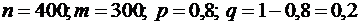 
. Тогда 
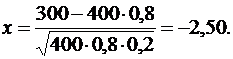По таблице значений функции 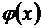находим, что 
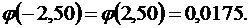Подставляя это значение в локальную формулу Муавра – Лапласа, получим:
.
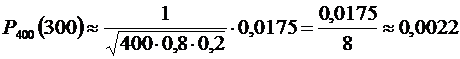Ответ: 0,0022.
5.По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины: а) наивероятнейшее число предприятий и вероятность этого числа; б) не менее 480.
Решение: а) по условию,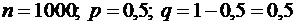 
. По формуле 
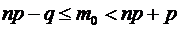, имеем:
;
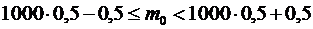то есть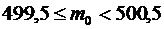 
. Итак, наивероятнейшее число предприятий равно 500. Теперь найдем вероятность этого числа по локальной формуле Муавра – Лапласа: 
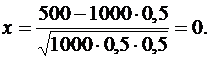Тогда
;
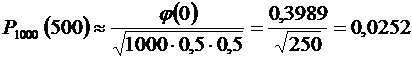б)необходимо найти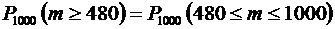 
. Применим интегральную формулу Муавра – Лапласа.
По условию,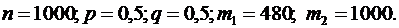 
Находим х1 и : 
, 
.
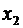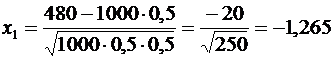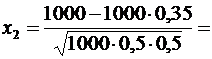
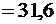По таблице значений функции 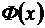, находим:
.
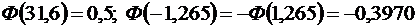Подставив эти значения в формулу, получим:
.
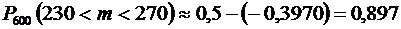Ответ: а) 0,0252; б) 0,897.
6.В страховой компании 10 тыс. клиентов. Страховой взнос каждого клиента составляет 500 руб. При наступлении страхового случая, вероятность которого по имеющимся данным и оценкам экспертов можно считать равной р = 0,005, страховая компания обязана выплатить клиенту страховую сумму размером 50 тыс. руб. На какую прибыль может рассчитывать страховая компания с надежностью 0,95?
Решение.Размер прибыли компании составляет разность между суммарным взносом клиентов и суммарной страховой суммой, выплаченной n0 клиентам при наступлении страхового случая, то есть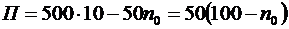 
тыс. руб.
Для определения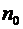 
воспользуемся интегральной формулой Муавра – Лапласа: 
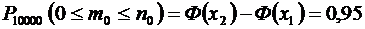, где m – число клиентов, которым будет выплачена страховая сумма; 
, 
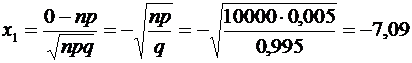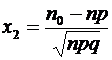, откуда
.
Из формулы Муавра – Лапласа имеем:
.
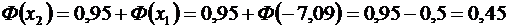По таблице значений функции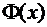 
, находим 
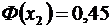при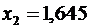 
. Теперь имеем: 
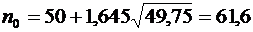и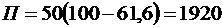 
. То есть с надежностью 0,95 ожидаемая прибыль составит 1,92 млн. руб.
Ответ: 1,92 млн. руб.
7.Вероятность приема сообщения без ошибок равна 0,5. Найти вероятность того, что из 100 принятых независимо друг от друга сообщений число принятых без ошибок будет отличаться от 50 по абсолютной величине не более, чем на 5.
Решение. В условиях задачи А: {сообщение принято без ошибок}.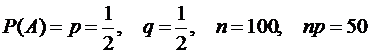 
. Необходимо найти 
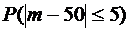. Применяем формулу (2):
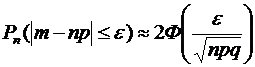, при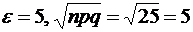 
, получим:
.
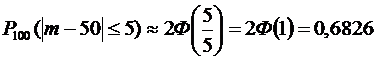Ответ: 0,6826.
8.Вероятность того, что деталь нестандартна, равна 0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности по абсолютной величине не более чем на 0,03.
Решение.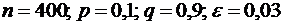 
. Требуется найти вероятность 
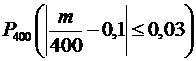. Пользуясь формулой (3)
,
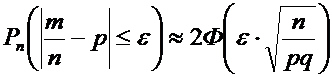имеем: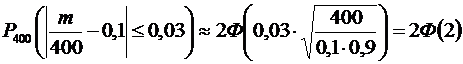 
.
По таблице значений функции 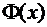, находим, что 
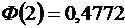. Следовательно, 
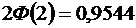. Итак, искомая вероятность приближенно равна 0,9544. Смысл: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности р = 0,1 по абсолютной величине не превысит 0,03.
9.Вероятность того, что деталь нестандартна, равна 0,1. Найти количество деталей, которые надо отобрать, чтобы с вероятностью равной 0,9544 можно было утверждать: относительная частота появления нестандартной детали отклонится от постоянной вероятности р по абсолютной величине не более чем на 0,03.
Решение. По условию,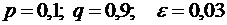 
;
.
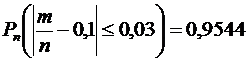Требуется найти n. Воспользуемся формулой из предыдущей задачи. В силу условия,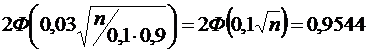 
. Значит, 
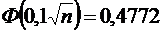. По таблице значений функции 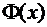, имеем: 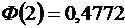. Для отыскания числа n получаем уравнение: 
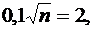значит, 
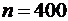. Если взять достаточно большое число проб по 400 деталей, то в 95,44 % этих проб будет отличаться от постоянной вероятности 
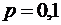по абсолютной величине не более, чем на 0,03, то есть относительная частота заключена в границах от 
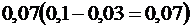до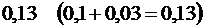 
. Другими словами, число нестандартных деталей в 95,44 % проб будет заключено между 28 (7 % от 400) и 52 (13 % от 400).
10.Пусть вероятность того, что покупателю необходима обувь 39-го размера, равна 0,3. Найти вероятность того, что среди 2000 покупателей таких будет от 570 до 630 включительно.
Решение. По условию, число испытаний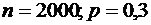 
, 
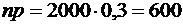. Значит, границы числа покупателей одинаково отличаются от произведения 
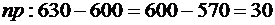. Поэтому для нахождения вероятности искомого события применяем формулу (2): 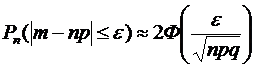. Получаем:
.
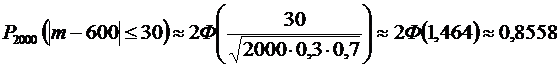Ответ: 0,8558.
11.Из условия предыдущего примера найти вероятность того, что отклонение доли нуждающихся в обуви 39-го размера от вероятности 0,3 не превзойдет 0,02.
Решение. По условию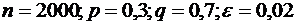 
. Искомая вероятность равна
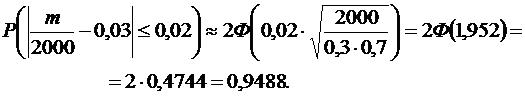
Ответ: 0,9488.
12.Вероятность того, что каждому из 800 покупателей необходима одежда 42-го размера, равна 0,3. Найти границы, в которых с вероятностью 0,9625 заключена доля покупателей, нуждающихся в одежде 42-го размера.
Решение. Подставляя значения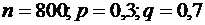 
и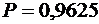 
в формулу 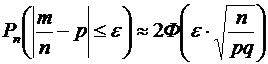, получим 
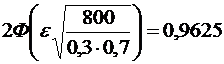. По таблице значений функции 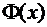, находим, что 
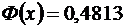при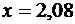 
. Значит, 
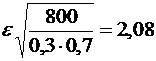, откуда 
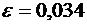. Итак, с вероятностью 0,9625 можно ожидать, что из 800 покупателей доля нуждающихся в одежде 42-го размера отклонится от вероятности 0,3 не более, чем на 0,034, то есть будет заключена в границах от 0,266 до 0,334.
Задачи для самостоятельного решения
1.При автоматической прессовке болванок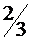 
их общего числа не имеют зазубрин. Найти вероятность того, что из 450 взятых наудачу болванок число болванок без зазубрин заключено между 280 и 320. (0,94257).
2.Штамповка клемм для соединительных пластин дает 20 % брака. Определить вероятность наличия от 100 до 125 клемм, не соответствующих стандарту, в партии из 600 клемм. (0,67).
3.На поле посеяно 1500 семян. Найти вероятность того, что всходы дадут 1200 семян, если вероятность того, что зерно взойдет, равна 0,9. (0,000054).
4.В лаборатории из партии семян, имеющих всхожесть 90 %, высеяно 600 семян. Найти вероятность того, что число семян, давших всходы, не менее 520 и не более 570. (0,99).
5.Из партии, в которой доля первосортных деталей равна 0,8, отобрано 60. Определить вероятность того, что 30 среди отобранных окажутся деталями первого сорта. (0).
6.Средний процент нарушений кинескопов у телевизоров в течение гарантийного срока равен 12 %. Вычислить вероятность того, что из 46 наблюдаемых телевизоров более 36 выдержат гарантийный срок. (0).
7.Стрелок сделал 30 выстрелов с вероятностью попадания при отдельном выстреле 0,3. Найти вероятность того, что при этом будет 8 попаданий. (0,3683).
8.В некотором пруду 80 % рыбы составляют карпы. Какова вероятность того, что из 9 выловленных 2 рыбы окажутся карпами? (0,00029).
9.При установившемся технологическом процессе фабрика выпускает в среднем 70 % продукции первого сорта. Чему равна вероятность того, что из тысячи выбранных изделий первосортных будет не менее 652 и не более 760? (0,999).
10.Какова вероятность того, что в столбике из 100 наугад отобранных монет число монет, расположенных гербом вверх, будет от 45 до 55? (0,6826).
11.Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян проросших будет от 790 до 830. (0,9736).
12.Вероятность поражения стрелком мишени при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз. (а) 0,7498; б) 0,1251).
13.Вероятность рождения мальчика равна 0,515. Найти вероятность того, что а) из 200 новорожденных будет 95 девочек; б) из 1000 новорожденных будет от 455 до 545 мальчиков. (а) 0,054; б) 0,9711).
14.Известно, что в среднем 60 % от всего числа изготовляемых телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется: а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов; б) 120 аппаратов первого сорта, если партия содержит 200 аппаратов? (а) 0,251; б) 0,0576).
15.Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50 % студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят: а) 180 студентов; б) не менее 180 студентов. (а) 0,0054; б) 0,977).
16.При обследовании уставных фондов банков выявлено, что пятая часть банков имеет уставной фонд свыше 100 млн. руб. Найти вероятность того, что среди 1800 банков имеют уставной фонд свыше 100 млн. руб.: а) не менее 300; б) от 300 до 400 включительно. (а) 0,998; б) 0,906).
17.Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из 750 покупателей не более 120 потребуют обувь этого размера. (0,003).
18.Предприятие имеет 2400 агрегатов. В каждый агрегат входит некоторая деталь, вероятность выхода, из строя которой за некоторое время равна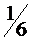 
. Исходя из этого, отдел снабжения заготовил за данное время 400 запасных деталей этого типа. Найти вероятность того, что такое количество запасных деталей обеспечит бесперебойную работу всех этих агрегатов в течение этого времени. (0,5).
19.Вероятность изделия быть бракованным равна 0,05. Сколько изделий надо взять, чтобы с вероятностью не меньшей 0,9, среди них оказалось не менее 50 бракованных? (1198).
20.Вероятность того, что деталь стандартна, равна р = 0,9. Найти: а) с вероятностью 0,9545 границы, в которых заключена доля стандартных среди проверенных 900 деталей; б) вероятность того, что доля нестандартных деталей среди них заключена в пределах от 0,09 до 0,11. (а)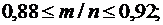 
б)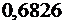 
).
21.Вероятность того, что дилер, торгующий ценными бумагами, продаст их, равна 0,7. Сколько должно быть ценных бумаг, чтобы можно было утверждать с вероятностью 0,996, что доля проданных среди них отклонится от 0,7 не более, чем на 0,04? (1089).
22.Вероятность поражения мишени при одном выстреле равна 0,6. Найти: а) границы числа попаданий в мишень при 600 выстрелах, чтобы вероятность невыхода за эти границы была равна 0,993; б) такое число выстрелов по мишени, при котором с вероятностью 0,993 можно ожидать, что отклонение частоты попаданий от вероятности 0,6 не превзойдет 0,03. (а)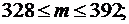 
б)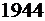 
).
23.Мастерская по гарантийному ремонту телевизоров обслуживает 2000 абонентов. Вероятность того, что купленный телевизор потребует гарантийного ремонта, равна 0,3. Предполагая, что событие, вероятность которого 0,9973, достоверно, найти границы числа телевизоров, которые потребуют гарантийного ремонта. (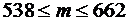 
).
24.Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях. (0,00967).
25.Проведено 700 независимых испытаний, в каждом из которых вероятность наступления события А равна 0,7. Найти вероятность того, что частота появления события окажется заключенной между 380 и 600. (1).
26.Найти вероятность того, что в партии из 800 изделий отклонение числа изделий первого сорта от наивероятнейшего числа не превысит по абсолютной величине 50, если вероятность появления изделия первого сорта равна 0,7. (1).
27.Вероятность попадания в мишень каждого из 700 выстрелов равна 0,4. Какое максимально возможное отклонение частоты от вероятности попадания при отдельном выстреле можно ожидать с вероятностью 0,997? (0,055).
28.Сколько нужно произвести опытов с бросанием монеты, чтобы с вероятностью 0,92 можно было ожидать отклонение частоты выпадения «герба» от теоретической вероятности 0,5 на абсолютную величину, меньшую, чем 0,01? (16512).
29.Вероятность появления успеха в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное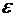 
, что бы с вероятностью 0,9876 абсолютная величина отклонения частоты появления успеха от его вероятности 0,8 не превысила 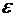. (0,05).
30.Найти приближенно границы, в которых число выпадения шестерки будет заключено с вероятностью 0,9973, если игральная кость брошена 80 раз. (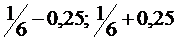 
).
Литература
1. Войтенко, М.А. Руководство к решению задач по теории вероятностей: учебное пособие для студентов 2 курса всех специальностей / М.А. Войтенко. – М.: изд. ВЗФЭИ, 1988. – 110 с.
2. Гмурман, В.Е. Теория вероятностей и математическая статистика: учебное пособие для вузов. 7-е изд., стер./ В.Е. Гмурман. – М.: Высш. шк., 2000. – 479 с.
3. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие для студентов вузов. 5-е изд., стер. / В.Е. Гмурман. – М.: Высш. шк., 2000. – 400 с.
4. Гнеденко, Б.В. Курс теории вероятностей / Б.В. Гнеденко. – 5-е изд. – М.: Наука, 1969. – 350 c.
5. Гурский, Е.И. Теория вероятностей с элементами математической статистики / Е.И. Гурский. – М.: Высшая школа, 1971. – 445 с.
6. Данко, П.Е. Высшая математика в упражнениях и задачах. Ч. II. / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 4-е изд. – М.: Высш. шк.,1986. – 415 с.
7. Карасев, А.И. Теория вероятностей и математическая статистика / А.И. Карасев. – М.: Статистика, 1979. – 423 с.
8. Колде, Я.К. Практикум по теории вероятностей и математической статистике: учебное пособие для студентов вузов / Я.К. Колде. – М.: Высш. шк., 1991. – 512 с.
9. Колемаев, В.А. и др. Теория вероятностей и математическая статистика / В.А. Колемаев. – М.: Высш. шк., 1991. – 351 с.
10. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов. 2-е изд., перераб. и доп. / Н.Ш. Кремер. – М.: ЮНИТИ, 2004. – 573 с.
11. Маркович, Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики / Э.С. Маркович. – М.: Высш. шк., 1972. – 479 с.
12. Четыркин, Е.М. Вероятность и статистика / Е.М. Четыркин, И.Л. Калихман. – М.: Финансы и статистика, 1992. – 523 с.
ПРИЛОЖЕНИЕ 1. Таблица значений функции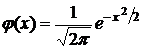 
Таблица П. 1. 1.
| 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 | |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3725 | 0,3712 | 0,3697 |
| 0,4 | 0,3683 | 0,3668 | 0,3653 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3521 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 | |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 |
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 | |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0355 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 |
| 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 | |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
| 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | |
| 4,1 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 |
| 4,2 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
| 4,3 | 0,00004 | 0,00004 | 0,00004 | 0,00003 | 0,00003 | 0,00003 | 0,00003 | 0,00003 | 0,00003 | 0,00003 |
| 4,4 | 0,00002 | 0,00002 | 0,00002 | 0,00002 | 0,00002 | 0,00002 | 0,00002 | 0,00002 | 0,00002 | 0,00002 |
| 4,5 | 0,00002 | 0,00002 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 |
| 4,6 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 | 0,00001 |
| 4,7 | 0,000006 | |||||||||
| 4,8 | 0,000004 |
ПРИЛОЖЕНИЕ 2. Таблица значений функции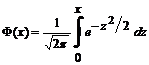 
Таблица П. 2. 1.
| 0,0000 | 0,0040 | 0,0080 | 0,0120 | 0,0160 | 0,0199 | 0,0239 | 0,0279 | 0,0319 | 0,0359 | |
| 0,1 | 0,0398 | 0,0438 | 0,0478 | 0,0517 | 0,0557 | 0,0596 | 0,0636 | 0,0675 | 0,0714 | 0,0753 |
| 0,2 | 0,0793 | 0,0832 | 0,0871 | 0,0910 | 0,0948 | 0,0987 | 0,1026 | 0,1064 | 0,1103 | 0,1141 |
| 0,3 | 0,1179 | 0,1217 | 0,1255 | 0,1293 | 0,1331 | 0,1368 | 0,1406 | 0,1443 | 0,1480 | 0,1517 |
| 0,4 | 0,1554 | 0,1591 | 0,1628 | 0,1664 | 0,1700 | 0,1736 | 0,1772 | 0,1808 | 0,1844 | 0,1879 |
| 0,5 | 0,1915 | 0,1950 | 0,1985 | 0,2019 | 0,2054 | 0,2088 | 0,2123 | 0,2157 | 0,2190 | 0,2224 |
| 0,6 | 0,2257 | 0,2291 | 0,2324 | 0,2357 | 0,2389 | 0,2422 | 0,2454 | 0,2486 | 0,2517 | 0,2549 |
| 0,7 | 0,2580 | 0,2611 | 0,2642 | 0,2673 | 0,2704 | 0,2734 | 0,2764 | 0,2794 | 0,2823 | 0,2852 |
| 0,8 | 0,2881 | 0,2910 | 0,2939 | 0,2967 | 0,2995 | 0,3023 | 0,3051 | 0,3078 | 0,3106 | 0,3133 |
| 0,9 | 0,3159 | 0,3186 | 0,3212 | 0,3238 | 0,3264 | 0,3289 | 0,3315 | 0,3340 | 0,3365 | 0,3389 |
| 0,3413 | 0,3438 | 0,3461 | 0,3485 | 0,3508 | 0,3531 | 0,3554 | 0,3577 | 0,3599 | 0,3621 | |
| 1,1 | 0,3643 | 0,3665 | 0,3686 | 0,3708 | 0,3729 | 0,3749 | 0,3770 | 0,3790 | 0,3810 | 0,3830 |
| 1,2 | 0,3849 | 0,3869 | 0,3888 | 0,3907 | 0,3925 | 0,3944 | 0,3962 | 0,3980 | 0,3997 | 0,4015 |
| 1,3 | 0,4032 | 0,4049 | 0,4066 | 0,4082 | 0,4099 | 0,4115 | 0,4131 | 0,4147 | 0,4162 | 0,4177 |
| 1,4 | 0,4192 | 0,4207 | 0,4222 | 0,4236 | 0,4251 | 0,4265 | 0,4279 | 0,4292 | 0,4306 | 0,4319 |
| 1,5 | 0,4332 | 0,4345 | 0,4357 | 0,4370 | 0,4382 | 0,4394 | 0,4406 | 0,4418 | 0,4429 | 0,4441 |
| 1,6 | 0,4452 | 0,4463 | 0,4474 | 0,4484 | 0,4495 | 0,4505 | 0,4515 | 0,4525 | 0,4535 | 0,4545 |
| 1,7 | 0,4554 | 0,4564 | 0,4573 | 0,4582 | 0,4591 | 0,4599 | 0,4608 | 0,4616 | 0,4625 | 0,4633 |
| 1,8 | 0,4641 | 0,4649 | 0,4656 | 0,4664 | 0,4671 | 0,4678 | 0,4686 | 0,4693 | 0,4699 | 0,4706 |
| 1,9 | 0,4713 | 0,4719 | 0,4726 | 0,4732 | 0,4738 | 0,4744 | 0,4750 | 0,4756 | 0,4761 | 0,4767 |
| 0,4772 | 0,4778 | 0,4783 | 0,4788 | 0,4793 | 0,4798 | 0,4803 | 0,4808 | 0,4812 | 0,4817 | |
| 2,1 | 0,4821 | 0,4826 | 0,4830 | 0,4834 | 0,4838 | 0,4842 | 0,4846 | 0,4850 | 0,4854 | 0,4857 |
| 2,2 | 0,4861 | 0,4864 | 0,4868 | 0,4871 | 0,4875 | 0,4878 | 0,4881 | 0,4884 | 0,4887 | 0,4890 |
| 2,3 | 0,4893 | 0,4896 | 0,4898 | 0,4901 | 0,4904 | 0,4906 | 0,4909 | 0,4911 | 0,4913 | 0,4916 |
| 2,4 |