А—действительная полуось, 2а—ось; в—мнимая полуось, 2в—ось.

F₁(-c;0), F₂(c;0) -- фокусы Г. 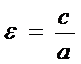-- эксцентриситет Г. .

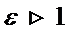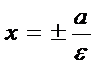--директрисы Г. 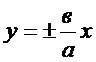--асимптоты Г. с²=а²+в²

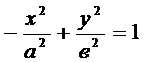--Г. ориентированная по оси Оу. х²-у²=а² –уравнение равносторонней Г.

18б. Где идут буквы с нулями-это значит,например X0,только в уменьшенном варианте где S,N-это вектора ,сверху палочку подрисуйте¯; √- этот корень всегда доводите до конца выражения

Парабола и ее геометрические свойства

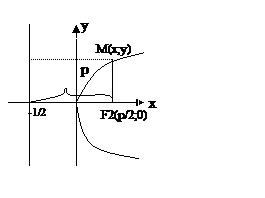
Параболой наз.геометрическое место точек плоскости,для к-х расстояние от заданной точки (F) до заданной прямой директрисы есть величина постоянная.

Исходя из определения расстояние от точки M до директрисы MK=MF,где MF=(x-p/2)²+y²=MK=x+p/2

x²-px+p²/4+y²-x²-px-p²/4=0

y²=2px -Каноническое уравнение параболы,ориентированной вдоль Оx,где p>0

аналагично получено x²=2py вдоль Оy

F (p/2;0)-в первом случае x=-p/2;

F(0;p/2)-во 2-ом случае y=-p/2;

Для эллипса эксцентриситет 0<E<1;

Для гиперболы E>1

Для параболы E=1;

19. Уравнение плоскости в пространстве. Условия параллельности и перепендикулярности двух плоскостей.

Ур-е в плоскости, проходящей через данную точку, перпендикулярно заданному вектору.Плоскость с нормальным вектором N={A, B, C}, проходящая через точку M0(x0, y0, z0):

A( x - x0) + B( y - y0) + C( z - z0) = 0.

Общее уравнение плоскости Ax+By+Cz+D=0

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости.

1. D = 0, Ax+By+Cz = 0 - плоск прох через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)

Если A=0, то By+Сz+D=0

Если B=0, то Ax +Сz+D=0

Если C=0, то Ax+By+D=0

Если A=B=0, то Сz+D=0

Если A=C=0, то By+D=0

Если A=D=0, то By+Сz=0

Если B=D=0, то Ay+Сz=0

A1A2+B1B2+C1C2=0 условие перпендикулярности

A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.

A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.

Пр линия в пр-ве.Параметрич ур-е прям.Канонич ур-е пр

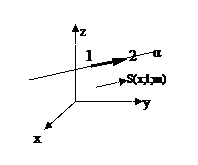
Это точка M0(x0,y0,z0)

Это точка M(x,y,z)

вектор M0M=(x-x0;y-y0;z-z0)

Векторы M0M//S

(x-x0)/k=(y-y0)/e=(t-t0)/m это каноническое

Введем параметр t Є R и положим (x-x0)/k=(y-y0)/e=(z-z0)/m=t, t Є R

x=x0+kt

y=y0+et это все параметрич ур-я прямой в пр-ве

z=z0+mt

Ур-я вида

A1x+B1y+C1Z+D1=0 это общие ур-я

A2x+B2y+C2Z+D2=0 прямой в пространстве

Они задают прямую ,как линию пересечения 2-х пл-тей

Взаимное расположение прямой и пл-ти в пр-ве

Пусть задана прямая каноническими ур-ми

(x-x0)/k=(y-y0)/e=(t-t0)/m

и плоскость общим ур-ем плоскости Ax+By+Cz+D=0

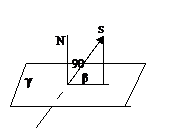
Дано:

S=(k,e,m)-направленный вектор прямой

N=(A,B,C)

Cos(90-β)=sinβ=(N,S)/|N|*|S|=(Ak+Be+Cm)/√ ²+B²+C²√k²+e²+m²

Условие парал-ти прямой к плоскости

Ak+Be+Cm=0

Условие перпенд-ти

Если пр перп-на пл-ти,то ее направл в-р S кол-н норм в-ру пл-ти S//N A/k=B/e=C/m

Условие принадлежности прямой к плоскости:

Ax0+By0+Cz0+D=0 Ak+Be+Cm=0

21. Предел числовой последовательности (ЧП).

ЧП – это ф-ия натур аргумента x_n=f(n),где n принадлежит N.

x_1, x_2,…x_n,…-числ послед.(1), x_n-общ член ЧП.

Число а наз пределом посл-ти, если для любого малого положит числа ξ > 0 сущ такой номер N, зависящий от ξ, что для всех номеров n>N выполняется неравенство |x_n-а|< ξ.

Замечание. |x_n-а|< ξ=> а- ξ<x₁<а+ ξ, X_n- ξ<a<x_n+ ξ – ξ окрестности т.а

Если число а-предел ЧП(1), то все члены посл-ти, начиная с некот номера N, попадают в ξ-окрестность т.а.Чем больше N,тем ниже а.

Если а-предел числ. послед-ти(1), то пишут: lim x_n=a или x_n→a, n→∞

Свойства числ. последовательности:

1.Если ЧП с общ членом x_n имеет предел, то она наз сходящейся.Всякая сход посл-ть огран, т.е. сущ M>0, что все члены этой П по модулю не превосх это число. |x_n |<М

2. Пусть заданы 3 П, x_n, y_n, z_n-общие члены. Причем lim x_n= lim z_n=а и выполняется неравенство: x_n ≤y_n≤z_n, то lim y_n=а.

3. Пусть послед. x_n, y_n имеют конечные пределы lim x_n=а lim y_n=в -∞<а,в<+∞. Тогда:

a) lim(x_n±y_n)= limx_n ± lim y_n)-справ для люб кон числа П

b) lim(x_n*y_n)= limx_n*limy_n

c) lim(Cx_n)=C limCx_n=C*a.

d) lim = = 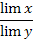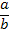, b≠0.

Посл α_n наз бескон малой, если ее предел = 0, т.е. limα_n=0

Послед. β_n наз бесконечно большой, если ее предел = ∞.

Утверждение.Если послед. α_n-беск. малая, то послед. - беск. большая и наоборот.В курсах матанализа док-ся, что П {Хn}= 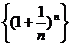монот и огранич.По теореме: для того, чтобы монот сходилась, необхмо и достаточно, чтобы она была огранич. След-но, эта П имеет предел. Он обозначается буквой е: е=lim 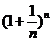, причем е=2,718.