Рассмотрим расширенную матрицу системы

A ―—”——

(А/В)=

~

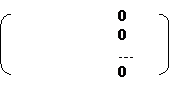След-но r(A/B) = r(A)

Док-ть, что СЛАУ совместна, если ранги равны.

b1 b2 br

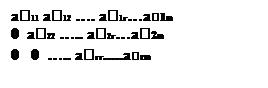Дано: r(A/B) = r(A) и к расшир матрице (A/B) применим преобраз-я Гаусса. В рез-те расшир матр (A/B) будет приведена к виду верхней треуг или трапециев. А тогда реш-я сист м. б. пол-ны обр м-м Г-са.

Случай 1. r(A)≠r(A/B), то СЛАУ несовместна.

Случай 2. r(A/B)=r(A)=n –СЛАУ совм и имеет единств реш-е.

Случай 3. r(A/B) = r(A)=r < –СЛАУ совм и имеет беск мн р-й.

Матричный метод

Пусть дана система из 3-х уравнений с тремя неизвестными 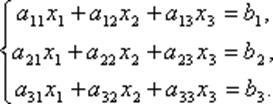. 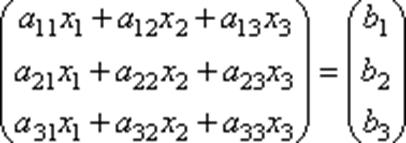Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.

Метод Крамера.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: 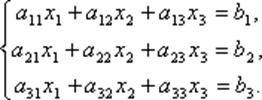Находим det

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов 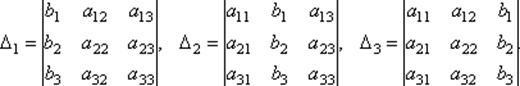Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём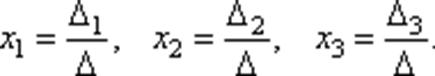

10.Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

· перестановка строк или столбцов;

· умножение строки на число, отличное от нуля;

· прибавление к одной строке другие строки.

· Удаление нулевой строки

Любая СЛАУ может быть преобразована к виду системы, у которой расширенная матрица будет иметь ступенчатый вид.

Приведение системы к ступенчатому виду или расширенную матрицу к виду трапециевидной называется прямой ход Гаусса. Обратный ход – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым. Придавая неизвестным (называемым свободными) произвольные значения, получим треугольную систему из которой последовательно найдем все остальные неизвестные (называемые базисными).

11. Понятие об n-мерном векторе. Векторное пространство.

Вектор – направленный отрезок на плоскости или в пространстве, имеющий определённую длину, у которого одна из точек принята за начало, а другая за конец. Длиной вектора (нормой) или модулем называется число, равное длине отрезка, изображающего вектор [ïaï=Öx2+y2(+z2)]. Если начало и конец вектора совпадают, то такой вектор называется нулевым и обозначается `0. Для каждого `а, отличного от 0, существует противоположный -`а, который имеет модуль, равный ïаï, коллиниарен с ним, но направлен в другую сторону. Два вектора `а и`в называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Два вектора называются равными, если они: 1)имеют равные модули; 2)коллиниарны; 3)направлены в одну сторону.

n-мерный вектор- упорядоченный набор n чисел, где каждое из n чисел- соответствующие координаты вектора. x=(x1,x2,xi,xn) Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее всем сво-вам суммы( коммутативное, ассоциативные), называется векторным пространством. Размерность векторного пространства равна количеству векторов в базисе этого пространства. Совокупность n-мерных векторов, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число, называется n-мерным координатным пространством. Система n—мерных лин. независимых векторов называется базисом Rn (R2-плоскость,R3-пространство), если каждый вектор этого пространства R разлагается по векторам этой системы. Базисом называется совокупность всех лин. независимых векторов системы пространства. Теорема: если диагональная система является частью n-мерных векторов, то она же является базисом этой системы. Теорема: любой вектор системы векторов единственным образов разлагается по векторам её базиса.

12.Линейная зависимость векторов.

Векторы 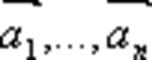называются линейно зависимыми, если существует такая линейная комбинация 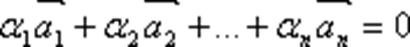при не равных нулю одновременно 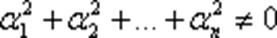. Если же только при ai = 0 выполняется 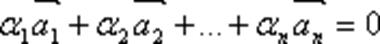, то векторы называются линейно независимыми.