Для транспортных специальностей
Сборник задач
Часть 1
Санкт-Петербург 2008
УДК 519.1(075.6)
ББК В183
С71
Рецензенты:
доктор технических наук, профессор, заведующий кафедрой высшей математики Балтийского государственного технического университета М. С. Попов;
кандидат технических наук, профессор, заведующий кафедрой высшей математики ПГУПС В. В. Гарбарук
|
Специальные разделы математики для транспортных специальностей : сборник задач. ч. 1 / В. Г. Дегтярев, Н. М. Репникова, И. А. Савушкина, Н. В. Шадринцева. – СПб.: Петербургский гос. ун-т путей сообщения, 2008. – 161 с.
В доступной для студентов форме излагаются основные элементы теории (кратко, без доказательств), приводится решение некоторого количества задач и примеров, а также типовые расчеты (примеры для самостоятельного решения) по следующим разделам дисциплины высшая математика: «Матрицы и определители», «Элементы векторной алгебры», «Элементы аналитической геометрии» и «Линейное программирование».
Пособие соответствует типовой программе Научно-методического совета по математике Министерства науки и образования РФ и может быть использовано студентами технических вузов в учебном процессе.
УДК 519.1(075.6)
ББК В183
© Петербургский государственный
университет путей сообщения,
| |
МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ И ДЕЙСТВИЯ НАД НИМИ
Матрицы и действия над ними.
Справочный материал.
1. Матрицей размера 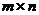 называется таблица чисел, содержащая
называется таблица чисел, содержащая 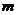 строк и
строк и 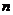 столбцов.
столбцов.
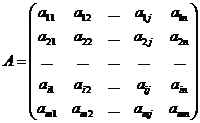 ,
,
где 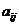 - элемент матрицы, стоящей в
- элемент матрицы, стоящей в 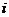 - ой строке и
- ой строке и 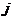 - ом столбце.
- ом столбце.
2. Если 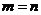 (т. е. число строк равно числу столбцов), то матрица называется квадратной порядка
(т. е. число строк равно числу столбцов), то матрица называется квадратной порядка 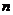 .
.
Элементы квадратной матрицы 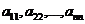 называются диагональными, а их совокупность образует главную диагональ.
называются диагональными, а их совокупность образует главную диагональ.
3. Сложение (вычитание) матриц одного и того же размера осуществляется поэлементно:
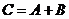 , если
, если 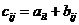 (
( 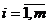 ;
; 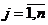 ).
).
4. При умножении матрицы на число – каждый элемент матрицы умножается на это число:
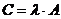 , если
, если 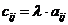 (
( 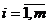 ;
; 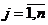 ).
).
5. Транспонирование матрицы – переход от матрицы  к матрице
к матрице 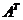 , в которой строки и столбцы поменялись местами с сохранением номеров.
, в которой строки и столбцы поменялись местами с сохранением номеров.
6. Умножение матрицы  на матрицу
на матрицу 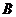 определено только тогда, когда число столбцов матрицы
определено только тогда, когда число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 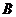 .
.
Тогда произведением матриц 
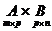 называется такая матрица
называется такая матрица 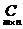 , каждый элемент которой
, каждый элемент которой 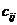 равен сумме произведений элементов
равен сумме произведений элементов 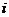 строки матрицы
строки матрицы  на соответствующие элементы
на соответствующие элементы 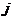 столбца матрицы
столбца матрицы 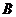 :
:
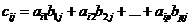 (
( 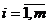 ;
; 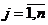 )
)
Примеры:
1. Даны матрицы 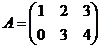 и
и 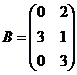 .
.
Найти 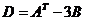 .
.
Решение: Найдем матрицу 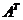 , транспонированную к
, транспонированную к  ,
, 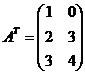 .
.
Найдем матрицу 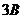 , умножив все элементы матрицы
, умножив все элементы матрицы 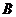 на 3.
на 3.
Проведем вычитание матриц 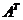 и
и 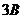 .
.
Таким образом:
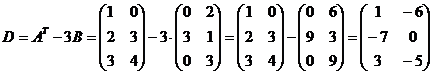 .
.
2. Даны матрицы 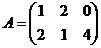 и
и 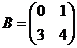 .
.
Найти 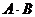 .
.
Решение: произведение матриц 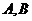 не определено, так как число столбцов матрицы
не определено, так как число столбцов матрицы  не равно числу строк матрицы
не равно числу строк матрицы 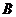 .
.
3. Даны матрицы 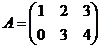 и
и 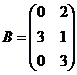 .
.
Найти 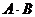 и
и 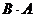
Решение:

áпо формуле (1)ñ 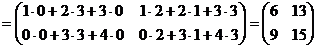 .
.
Аналогично:
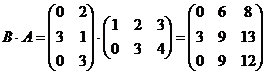 .
.
Следует обратить внимание на то, что в общем случае, произведение матриц не коммутативно, то есть: 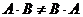 .
.
Задачи для самостоятельного решения.
I. Выполнить действия.
1. Найти матрицу 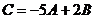 , если
, если
а. 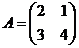 и
и 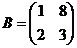 .
.
б. 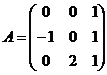 и
и 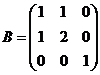 .
.
Найти 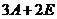 , где
, где 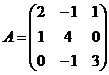 , а
, а 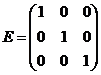 .
.
2. Проверить, что 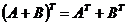 , если
, если 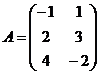 и
и 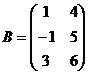 .
.
3. Даны матрицы 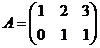 и
и 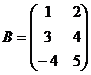 .
.
Найти
а. 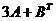 .
.
б. 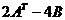 .
.
II. Найти произведения матриц.
1. 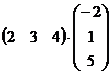 .
.
2. 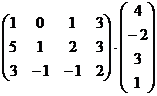 .
.
3. 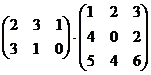 .
.
4. 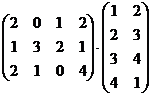 .
.
5. 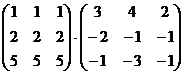 .
.
6. 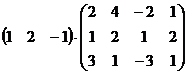 .
.
III. Проверить перестановочность матриц.
1. 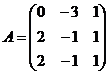 и
и 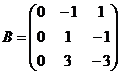 .
.
2. 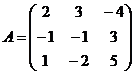 и
и 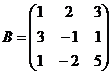 .
.
VI. Решить матричные уравнения.
1. 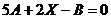 , если
, если 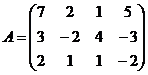 и
и 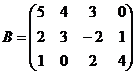 .
.
2. 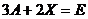 , если
, если 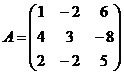 и
и 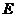 - единичная матрица 3-го порядка.
- единичная матрица 3-го порядка.
3. 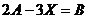 , если
, если 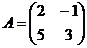 и
и 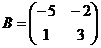 .
.
1.2. Определители квадратных матриц.
Справочный материал.
1. Определителем матрицы второго порядка называется число:
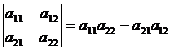 (1)
(1)
2. Определителем матрицы третьего порядка называется число:
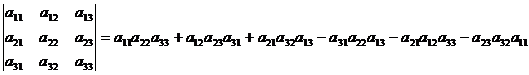 (2)
(2)
3. Определителем квадратной матрицы 
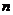 -го порядка называется число, которое ставится в соответствие данной матрице по определенному правилу, которое будет приведено ниже.
-го порядка называется число, которое ставится в соответствие данной матрице по определенному правилу, которое будет приведено ниже.
Определитель 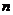 –го порядка обозначается:
–го порядка обозначается:
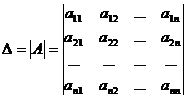
4. Минором 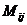 элемента
элемента 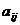 определителя
определителя 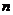 –го порядка называется определитель
–го порядка называется определитель 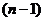 - го порядка, полученный из данного вычеркиванием
- го порядка, полученный из данного вычеркиванием 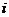 –ой строки и
–ой строки и 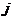 –ого столбца.
–ого столбца.
5. Алгебраическим дополнением 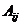 элемента
элемента 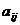 называется число, которое находится по формуле:
называется число, которое находится по формуле:
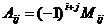
Замечание:
Здесь и далее, говоря об элементах, строках или столбцах определителя, мы будем иметь ввиду элементы, строки или столбцы соответствующей матрицы.
6. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
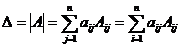 (3)
(3)
Равенство (3) называется разложением определителя по элементам 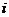 – ой строки или по j- му столбцу.
– ой строки или по j- му столбцу.
7. Определитель треугольной и, в частности, диагональной матрицы равен произведению ее диагональных элементов.
8. Некоторые свойства определителей:
8.1. Определитель не изменится при транспонировании матрицы.
8.2. Определитель не изменится, если к элементам какой либо строки определителя прибавить соответствующие элементы другой строки, умноженные на число, отличное от нуля.
8.3. Определитель равен нулю, если:
· Все элементы какой либо строки равны нулю.
· Элементы любых двух строк пропорциональны либо, в частном случае, равны.
Перечисленные свойства справедливы и для столбцов.
Примеры:
1. Вычислить определители:
 ;
; 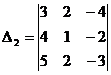 .
.
Решение:
Согласно формуле (1)
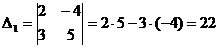
Выражение (2) можно получить следующим образом. Припишем справа к таблице элементов определителя первые два столбца. Со знаком «+» в сумму (2) входят произведения элементов, стоящих на главной диагонали и на прямых, параллельных этой диагонали. Слагаемые со знаком «-» получаются аналогично по отношению к побочной диагонали.
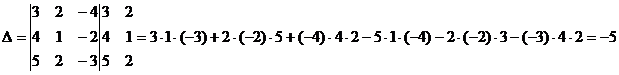
2. Найти минор и алгебраическое дополнение элемента 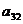 определителя
определителя
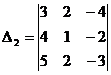 .
.

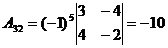
Вычислить определитель 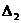 , разложив его по элементам первой строки
, разложив его по элементам первой строки
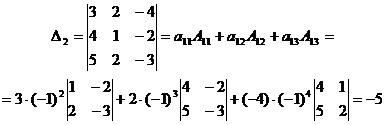
Задачи для самостоятельного решения.
1. Вычислить определитель второго порядка:
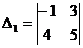 ,
, 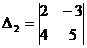 ,
, 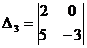 .
.
2. Вычислить определитель третьего порядка:
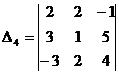 ,
, 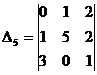 .
.
3. Определить, при каких значениях 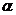 определители не равны нулю.
определители не равны нулю.
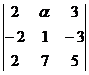 ,
, 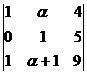 .
.
4. Решить уравнения:
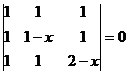 ,
, 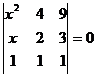
Обратная матрица.
Справочный материал.
1. Квадратная матрица 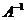 называется обратной для квадратной матрицы
называется обратной для квадратной матрицы  того же порядка, если
того же порядка, если
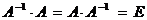 , (1)
, (1)
где Е – единичная матрица того же порядка, что и матрица А.
2. Квадратная матрица  называется невырожденной (или неособенной), если ее определитель отличен от нуля, т.е.
называется невырожденной (или неособенной), если ее определитель отличен от нуля, т.е. 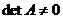 .
.
3. Обратная матрица 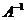 существует и единственна тогда и только тогда, когда исходная матрица
существует и единственна тогда и только тогда, когда исходная матрица  невырожденная, т. е.
невырожденная, т. е. 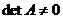 .
.
В этом случае ее можно найти по формуле:
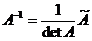 ,
,
где 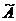 - присоединенная матрица, элементы которой
- присоединенная матрица, элементы которой 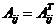 равны алгебраическим дополнениям элементов матрицы
равны алгебраическим дополнениям элементов матрицы 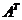 , транспонированной к матрице
, транспонированной к матрице  , т.е.
, т.е.
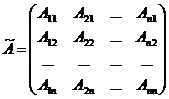 .
.
Примеры:
1. Выяснить, является ли матрица 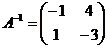 обратной к матрице
обратной к матрице 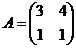 .
.
Решение:
Найдем произведения 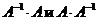 .
.
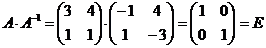
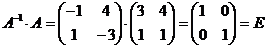
В соответствии с определением (1) данные матрицы являются взаимно обратными.
2. Определить, имеют ли данные матрицы обратные:
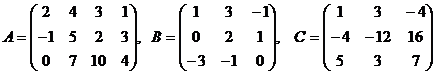 .
.
Решение:
Матрица  обратной не имеет, т. к. она не квадратная (ее размер
обратной не имеет, т. к. она не квадратная (ее размер 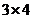 ).
).
Матрица 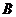 имеет обратную, т. к. ее определитель
имеет обратную, т. к. ее определитель 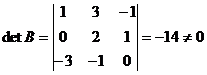 .
.
Матрица 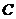 обратной не имеет, т. к. определитель этой матрицы
обратной не имеет, т. к. определитель этой матрицы 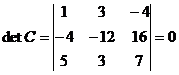
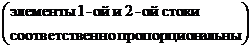 .
.
3. Найти матрицу, обратную к данной 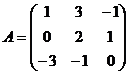 .
.
Решение:
· Найдем определитель матрицы  :
: 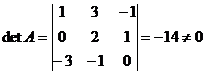 .
.
Так как 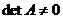 , следовательно, матрица
, следовательно, матрица  имеет обратную.
имеет обратную.
Напомним, что обратная матрица  вычисляется по формуле:
вычисляется по формуле:
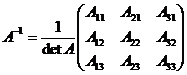 , (1)
, (1)
где 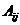 алгебраические дополнения элементов
алгебраические дополнения элементов 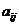 матрицы
матрицы  .
.
· Найдем алгебраические дополнения элементов матрицы  :
:
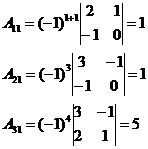
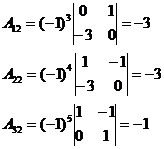
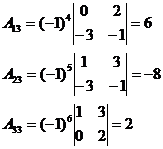
· Находим обратную матрицу по формуле (1):
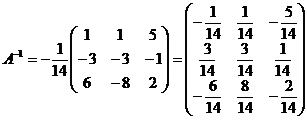 .
.
· Проверим правильность вычисления обратной матрицы:
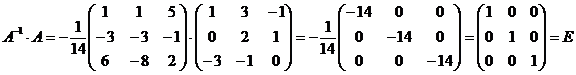
Задачи для самостоятельного решения:
1. Вычислить, какие из приведенных матриц имеют обратные.
· 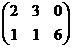 .
.
· 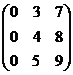 .
.
· 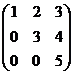 .
.
· 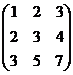 .
.
2. Для следующих матриц найти обратные:
· 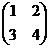 .
.
· 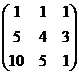 .
.
· 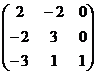 .
.
3. Решить матричные уравнения:
· 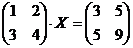
· 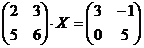 .
.
Указание: Х – квадратная матрица второго порядка.
Исходное матричное уравнение имеет вид 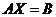 .
.
Для нахождения матрицы Х достаточно умножить обе части исходного
уравнения на 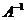 слева
слева 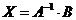 .
.
4. Выполнить действия 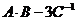 , где
, где 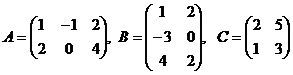 .
.
5. Найти матрицу 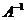 , обратную к матрице
, обратную к матрице 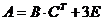 , где
, где
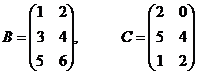 ,
, 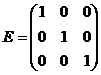 .
.
Ранг матрицы.
Справочный материал.
1. Рангом матрицы 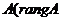 или
или 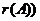 называется максимальный порядок отличных от нуля миноров этой матрицы.
называется максимальный порядок отличных от нуля миноров этой матрицы.
· Ранг прямоугольной матрицы 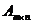 удовлетворяет неравенству:
удовлетворяет неравенству:
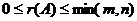 .
.
· Если матрица  - квадратная порядка
- квадратная порядка 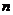 , то
, то 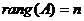 тогда и только тогда, когда
тогда и только тогда, когда 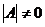 .
.
2. Элементарные преобразования, не меняющие ранга матрицы
· Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
· Прибавление к элементам какой либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на некоторое число
· Перестановка двух строк (столбцов) матрицы.
· Транспонирование матрицы.
· Отбрасывание нулевой строки (столбца).
3. С помощью элементарных преобразований матрицу 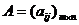 приводят к ступенчатому виду:
приводят к ступенчатому виду:
 , где
, где
все диагональные элементы 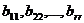 , отличные от нуля, а элементы, расположенные ниже диагональных элементов равны нулю.
, отличные от нуля, а элементы, расположенные ниже диагональных элементов равны нулю.
Так как минор 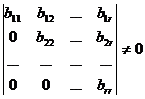 , то ранг ступенчатой матрицы
, то ранг ступенчатой матрицы 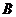 равен
равен 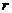
(т.е. числу ненулевых строк ступенчатой матрицы B).
4. Базисный минор – это не равный нулю минор, порядок которого равен рангу матрицы. Матрица может иметь несколько базисных миноров.
Пример.
Найти ранг матрицы и указать один из базисных миноров.
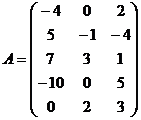
Решение: матрица имеет размер 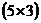 ,
, 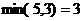 , значит
, значит 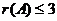 .
.
С помощью элементарных преобразований приведем матрицу к ступенчатому виду.
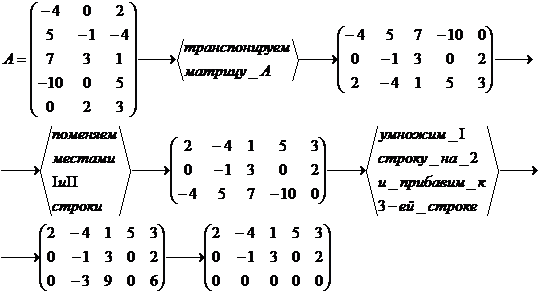
Получили ступенчатую матрицу, у которой две ненулевые строки.
Таким образом ранг исходной матрицы А равен двум.
Выделенный минор может быть выбран в качестве базисного.
Задачи для самостоятельного решения:
Найти с помощью элементарных преобразований ранг матрицы:
1. 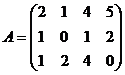 2.
2. 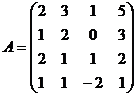 3.
3. 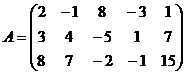
4. 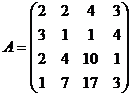 5.
5. 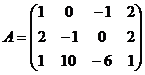 6.
6. 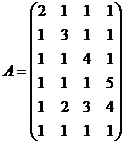 .
.
