D – разбиение плоскости одного параметра

Пример. Построить границу D – разбиения по коэффициенту усиления K для системы автоматического регулирования, передаточная функция которой в разомкнутом состоянии имеет вид:

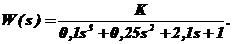
Решение:

Передаточная функция в замкнутом состоянии:

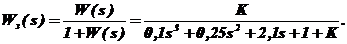
Характеристическое уравнение

D(s) =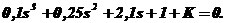

Уравнение границы D – разбиения получим, подставляя 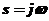в характеристическое уравнение

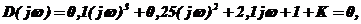
из которого находим K

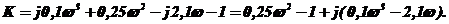
Выделим вещественную и мнимую часть:

вещественная часть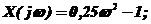

мнимая часть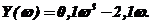

Задаваясь различными значениями 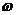, находим 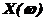и .

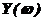Таблица Е1 – Расчет границы D-разбиения

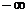		-5	-4	-2	-1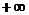
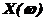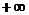		5,25			-0,75	-1	-0,75			5,25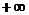
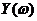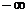		-2		3,4			-2	-3,4	-2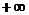

По полученным значениям строим кривую D – разбиения.

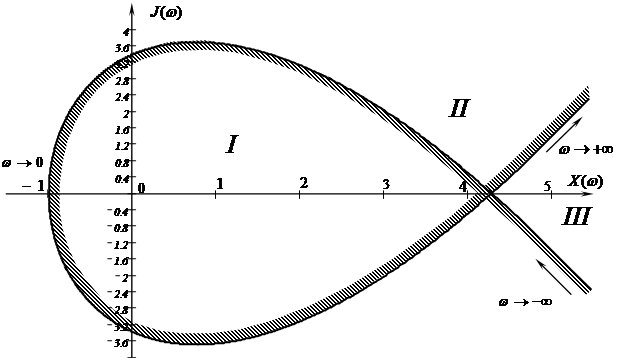Рисунок Е1 – Кривая D-разбиения плоскости одного параметра

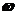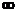Заштрихуем её, пользуясь правилом штриховки: двигаясь по кривой D-разбиения при изменении частоты от - до + 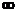, наносим штриховку слева.

Комплексная плоскость 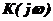разбивается кривой D-разбиения на 3 области: I, II, III.

Областью – претендентом является область I, так как штриховка направлена внутрь ее.

Проверяем, является ли область I областью устойчивости.

Возьмём любое К в этой области, например, К=1. Подставим его в характеристическое уравнение:

.

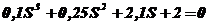Определяем устойчивость системы, пользуясь критерием Гурвица.

Главный определитель Гурвица:

.

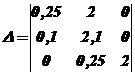Диагональные миноры:

;

.

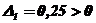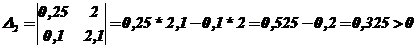Все диагональные миноры положительны, система устойчива.

При К=1 система устойчива, следовательно, область I будет областью устойчивости (число правых корней равно 0), т.е. при любом 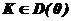, система будет устойчивой. Область реальных значений, при которых система будет устойчива, ограничивается положительными вещественными значениями 0<К<4,25.

Пользуясь правилами перехода, определим число правых корней m в области II и III. В области II m =1, так как при переходе из области I в область II граница D-разбиения пересекается против штриховки. В области III m=2. Таким образом, имеем области D(0), D(1), D(2). Область D(3)в данном случае отсутствует. Это означает, что при заданных параметрах системы и любом значении К, невозможно, чтобы все три корня характеристического уравнения одновременно были правыми.

Приложение З

(обязательное)

Контрольные вопросы

1 Для какой цели используется преобразование Лапласа

2 Объясните понятия оригинал, изображение функции по Лапласу

3 В чем суть прямого и обратного преобразования Лапласа

4 Дайте определение передаточной функции в изображениях Лапласа

5 Методика получения передаточной функции в изображениях Лапласа

6 Какие свойства преобразования Лапласа используются при определении передаточной функции по дифференциальному уравнению

7 Передаточные функции типовых звеньев, что означают символы, входящие в выражения для передаточных функций

8 Назовите виды частотных характеристик

9 Объясните понятия амплитуда, фаза, частота гармонического сигнала

10 Физический смысл частотных характеристик

11 Как получить частотную передаточную функцию

12 Амплитудная частотная характеристика

13 Фазовая частотная характеристика

14 Амплитудные частотные характеристики типовых звеньев

15 Фазовые частотные характеристики типовых звеньев

16 АФЧХ, методика ее расчета и построения

17 Логарифмические частотные характеристики

18 Какие преимущества и особенности представления частотных свойств в виде логарифмических частотных характеристик

19 Что такое декада, децибел

20 Формула, связывающая ЛАЧХ и амплитудную частотную характеристику

21 Методика построения асимптотической ЛАЧХ

22 Как по АФЧХ определить значение амплитуды фазы на заданной частоте

23 Что означает наклон ЛАЧХ ±20 дБ/дек, ±40 дБ/дек и какими звеньями он обусловлен

24 Объясните понятия структурной схемы системы автоматического управления

25 Типовые соединения звеньев в структурных схемах и их передаточные функции

26 Что представляют собой перекрестные связи в структурных схемах и каким образом от них избавляются

27 Правила перестановки сумматоров и узлов

28 Правила переноса сумматоров и узлов через звенья

29 Объясните понятия разомкнутой и замкнутой системы

30 Как получить характеристическое уравнение для анализа устойчивости замкнутой системы

31 Анализ устойчивости системы с помощью критерия Рауса

32 Понятие D-разбиения

33 Как построить границу D-разбиения

34 Как на плоскости D-разбиения выделить область устойчивости

35 Как убедиться, что область-претендент на устойчивость является действительно областью устойчивости

Г.И.Чмых

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Методические указания

по выполнению контрольной работы

для студентов направления подготовки 15.03.04

«Автоматизация технологических процессов и производств»

профиля «Автоматизация технологических процессов

и производств в химической отрасли»

заочной формы обучения

Электронное издание

Редакционно-издательский центр СибГТУ

660049 Красноярск, пр. Мира, 82

Телефон (319) 227-67-90

Факс (319) 211-97-25