Расчет и построение логарифмических частотных характеристик

Для построения логарифмических амплитудной и фазовой частотных характеристик системы с произвольной дробно-рациональной передаточной функцией 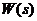(3.3) нужно ее числитель и знаменатель разложить на элементарные множители и представить в виде

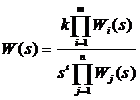, (3.8)

где k - общий коэффициент передачи системы; 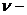число интегрирующих звеньев ν=…,-1,0,1,2,..; W_i(s), W_j(s) представляют собой элементарные множители 1-го и 2-го порядка с единичными коэффициентами усиления, т.е множители вида s, 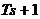, , 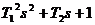если 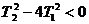. Множителю s в знаменателе соответствует интегрирующее звено, множителю 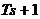в знаменателе соответствует инерционное звено (апериодическое первого порядка), множителю 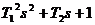в знаменателе, если 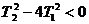, соответствует колебательное звено. Если эти множители стоят в числителе передаточной функции, то им соответствую звенья: идеальное дифференцирующее, форсирующее первого порядка и форсирующее второго порядка. Поскольку заданные передаточные функции (таблица 3.1) представляют собой произведение передаточных функций типовых звеньев, операцию разложения на простые множители выполнять не нужно.

Подставляя в (3.8) 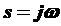, получим частотную передаточную функцию

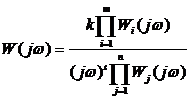. (3.9)

В соответствии с (3.3) и (3.9) ЛАЧХ

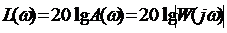. 3.10)

При вычислении амплитудной и фазовой частотных функций удобно использовать следующие правила вычисления модуля и аргумента произведения и отношения комплексных чисел (функций):

модуль произведения комплексных чисел равен произведению модулей сомножителей;

аргумент произведения комплексных чисел равен сумме аргументов сомножителей;

модуль отношения комплексных чисел равен отношению модулей числителя и знаменателя;

аргумент отношения комплексных чисел равен разности аргументов числителя и знаменателя.

В соответствии с правилами вычисления модуля амплитудную частотную функцию системы, имеющей частотную передаточную функцию вида (3.9), можно представить

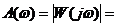
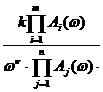. (3.11)

Из (3.10) и (3.11) имеем для ЛАЧХ выражение

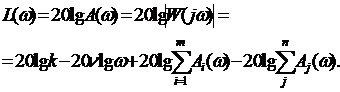(3.12)

Фазовая частотная функция в соответствии с правилом вычисления аргумента комплексной функции определяется выражением

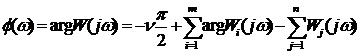. (3.13)

Таким образом, ЛАЧХ при любой передаточной функции может быть получена сложением или вычитанием амплитуд (в дБ), а ЛФЧХ путем сложения или вычитания фаз простых сомножителей.

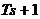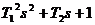Простым множителям s, и в передаточной функции соответствуют множители jω, 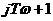и 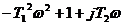в частотной передаточной функции. Соответствующие амплитудные частотные функции

, ,

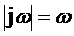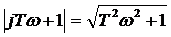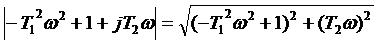. (3.14)

Фазовые частотные функции в радианах:

интегратора ;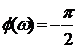

инерционного звена ;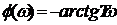

колебательного звена 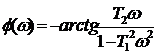для частот от нуля до ;

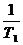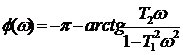для частот ;

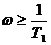идеального дифференцирующего звена ;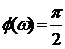

;форсирующего звена первого порядка ;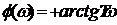

форсирующего звена второго порядка ,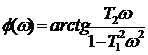

Для перевода 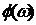в градусынеобходимо полученные значения умножить 57,32.

По формулам (3.12 и 1.13), изменяя частоту, можно построить точные характеристики ЛАЧХ и ЛФЧХ. При этом нужно иметь в виду, что при 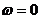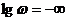. Поэтому в начале координат откладывается произвольная частота 10^k, где k =…-2,-1,0,1… . Эта частота выбирается примерно меньше на одну-две декады, чем частота 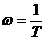, где 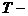наибольшая из постоянных времени звеньев, входящих в систему, для которой определяются частотные характеристики.

Для упрощения построения монотонная ЛАЧХ аппроксимируется ломаной линией, состоящей из прямолинейных отрезков с типовыми наклонами: 0, 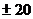, , 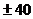… дБ/дек. Такие характеристики называются асимптотическими. При этом нужно учитывать следующее:

1. Усилительное звено имеет 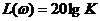, его ЛАЧХ представляет горизонтальную линию, фазовая характеристика 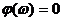рад совпадает с осью частот.

2. Сомножитель 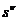, где 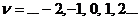имеет амплитудную характеристику 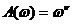, 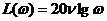. ЛАЧХ представляет прямую линию с наклоном, равным 20 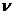дБ/дек. Фазовая характеристика постоянная и определяется выражением .

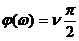3. Сомножитель 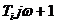в числителе (3,9) соответствует форсирующему звену и имеет амплитудную частотную характеристику 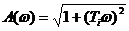и ЛАЧХ 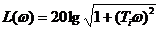. Асимптотическая ЛАЧХ состоит из двух асимптот: низкочастотной и высокочастотной.

Низкочастотная асимптота соответствует условию 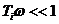. При этом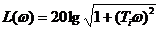 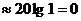(под корнем пренебрегаем слагаемым 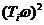), т.е. для низких частот ЛАЧХ - горизонтальная прямая, совпадающая с осью абсцисс.

Высокочастотная асимптота соответствует условию 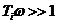. При этом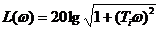 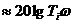(под корнем пренебрегаем единицей), т.е. для высоких частот ЛАЧХ – прямая линия с наклоном +20 дБ/дек, которая пересекает горизонтальную ось на частоте 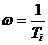. Эта частота называется сопрягающей.

Фазовая частотная функция 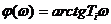. На низких частотах ФЧХ стремится к нулю, на сопрягающей частоте 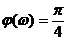рад, на частотах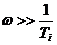 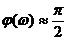рад.

4. Сомножитель 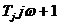в знаменателе (3,9) соответствует инерционному звену с коэффициентом передачи, равным единице. Его амплитудная частотная характеристика

,

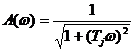а ЛАЧХ .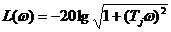

При 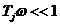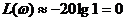, т.е. низкочастотная асимптота – горизонтальная прямая, совпадающая с осью абсцисс.

При 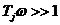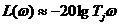, т.е. высокочастотная асимптота – прямая линия с наклоном – 20 дБ/дек, пересекающая ось абсцисс на частоте .

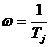Фазовая частотная функция 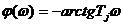и изменяется в пределах от 0 до 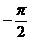рад. На сопрягающей частоте 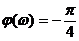рад.

5. Сомножитель 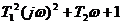в знаменателе (3.9) соответствует колебательному звену с коэффициентом передачи, равным1.

Амплитудная частотная функция этого звена

,

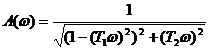а логарифмическая амплитудная частотная функция

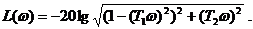
Для 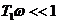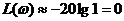, следовательно, низкочастотная асимптота - горизонтальная прямая, совпадающая с осью абсцисс.

Для 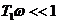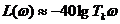, следовательно, высокочастотная асимптота представляет прямую линию с наклоном – 40дБ/дек, которая пересекает ось абсцисс на частоте .

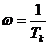Фазовая частотная функция

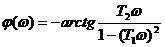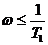для ;

для 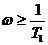.