Частотные функции и характеристики

Частотные характеристики динамических звеньев могут быть найдены из передаточных функций, если в них положить 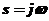. Функцию 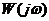, которая получается путём подстановки в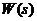 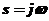называют частотной передаточной функцией. Она является комплекснозначной функцией от вещественной переменной 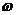, называемой частотой.

Частотную передаточную функцию можно представить в виде

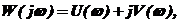(3.1)

где 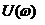- вещественная часть,

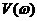- мнимая часть частотной передаточной функции.

Частотную передаточную функцию можно представить в показательной форме

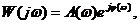(3.2)

где 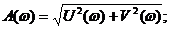- амплитудная частотная функция ( модуль частотной передаточной функции);

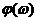- аргумент частотной передаточной функции

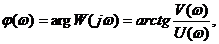если .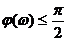

Частотную передаточную функцию (2.8) называют также амплитудно-фазовой частотной функцией.

Годограф вектора функции 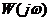на комплексной плоскости в координатах U( 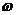),V( 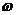) (рисунок 3.1) называется амплитудно-фазовой частотной характеристикой (АФЧХ). Любой частоте 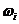соответствует некоторая точка А с координатами .

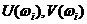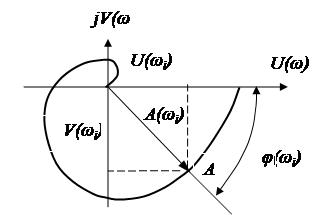
Рисунок 3.1 – Амплитудно-фазовая частотная характеристика

Длина вектора ОА, проведенного из начала координат в эту точку, равна значению амплитудно-частотной функции 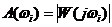, а угол 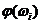, образованный этим вектором с положительной действительной полуосью равен аргументу 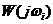, т.е. значению фазовой частотной функции на частоте .

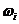Кроме перечисленных частотных характеристик, при анализе систем используются логарифмические частотные характеристики (ЛЧХ) – логарифмические амплитудные частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ).

Логарифмической амплитудной частотной функцией называют функцию

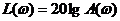, (3.3)

а график в зависимости от логарифма частоты называют логарифмической амплитудной частотной характеристикой. Единицей является децибел, дБ. Измерение модуля 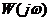в децибелах имеет ряд преимуществ: возможность изображения 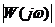в большом диапазоне амплитуд с достаточной точностью; возможность получать простые аппроксимации для 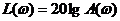; ЛАЧХ для последовательного соединения звеньев может быть получена суммированием ЛАЧХ отдельных звеньев.

Логарифмической фазовой частотной характеристикой называют график функции 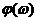в зависимости от логарифма частоты.

При построении логарифмических частотных характеристик по оси абсцисс откладывают частоту в логарифмическом масштабе. Преимущества использования логарифмической шкалы: ось абсцисс линейна относительно 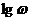, частотные характеристики можно представлять в широком диапазоне частот. Единица частоты на логарифмической шкале – декада. Декада – расстояние между частотам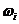и и 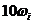для любого значения 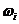. При этом на отметке, соответствующей 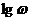, записывают действительное значение частоты 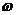. По оси ординат откладывается 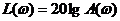в децибелах (дБ).

При построении ЛФЧХ по оси абсцисс, так же как и при построении ЛАЧХ, откладывается частота в логарифмическом масштабе. По оси ординат откладывается фазовый сдвиг в линейном масштабе в радианах или градусах.

Логарифмические амплитудную и фазовую характеристики принято изображать друг под другом с одинаковыми осями абсцисс.

Расчет и построение АФЧХ

Передаточная функция динамического элемента или системы в изображениях Лапласа в общем виде:

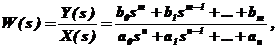(3.3)

где 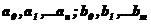- постоянные коэффициенты, зависящие от параметров звеньев (постоянных времени и коэффициентов передачи);

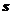- оператор Лапласа.

Выполнив подстановку 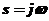в (3.3), получим комплексный коэффициент передачи частотную передаточную функцию):

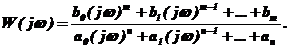(3.4)

В выражении (3.4) выделяем вещественную и мнимую части

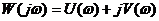. (3.5)

Для определения вещественной 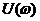и мнимой 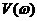частей запишем выражение (3.4) в виде

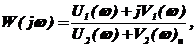(3.6)

где 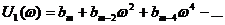- вещественная часть числителя (3.4);

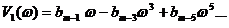- мнимая часть числителя (3.4);

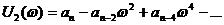- вещественная часть знаменателя (3.4);

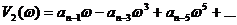. – мнимая часть знаменателя (3.4).

С учетом (3.6) получим

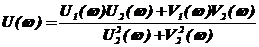; (3.6)

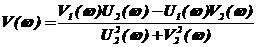. (3.7)

По зависимости (3.5) амплитудно-фазовая частотная характеристика строится в декартовой системе координат, где по оси абсцисс откладывается вещественная часть, а по оси ординат мнимая часть. Любой частоте ω_i будет соответствовать точка с координатами [U(ω_i), jV(ω_i)]. Соединяя точки, полученные при различных значениях частоты, получим годограф (амплитудно-фазовую частотную характеристику или АФЧХ).

Для построения АФЧХ необходимо:

1) изучить теоретический материал по теме, изложенный на с.40-64 [1], уяснить понятия динамического звена, типового звена, передаточной функции, частотной передаточной функции, ознакомиться с методикой получения и построения АФЧХ по передаточной функции;

2) выписать передаточную функцию динамического звена и его параметры согласно заданному варианту;

3) выяснить, какие элементарные звенья входят в состав анализируемого динамического звена.

Решение задачи рекомендуется выполнять в последовательности:

1) преобразовать передаточную функцию к виду (3.3);

2) получить частотную передаточную функцию (3.4);

3) определить вещественную и мнимую части частотной передаточной функции, пользуясь формулами (3.6, 3.7);

4) рассчитать координаты АФЧХ U(ω_i) и V(ω_i), изменяя частоту ω от 0 до ∞;

5) результаты расчета оформить в таблице;

6) по результатам расчета построить АФЧХ в декартовой системе координат.

При расчете АФЧХ определяют ее координаты при предельных значениях частоты ( 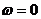и 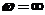), при частотах 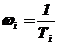, где 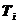- постоянные времени звеньев. Затем вычисляются дополнительные точки для более точного построения АФЧХ. Если в составе динамического звена

имеются интегрирующие звенья, то при ω=0 частотная передаточная функция обращается в 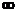, а АФЧХ претерпевает разрыв. Пример решения задачи приведен в Приложении Б.