Независимыми называются события A и B, если вероятность события A не зависит от того, наступило событие B или нет.

Если вероятность наступления события A зависит от того, наступило событие B или нет, события называютзависимыми и вводят понятие условной вероятности.

· Условной вероятностью события A при условии того, что произошло событие B, называют величину 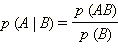. Соответственно, для зависимых событийp (AB) = p (B) p (A | B).

44. Теорема умножения вероятностей.

Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

Если события независимые, то , и теорема умножения вероятностей принимает вид:

В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.

Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.

Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

45. Формула полной вероятности.

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

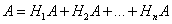
Применяя аксиому сложения вероятностей, имеем

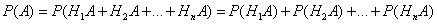
Но 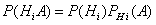(i=1, 2, ..., n), поэтому

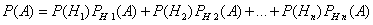46. Формула Байеса.

Пусть 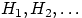— полная группа событий, и 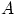— некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие 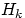, если в результате эксперимента наблюдалось событие 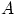, может быть вычислена по формуле:

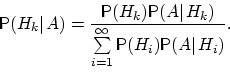По определению условной вероятности,

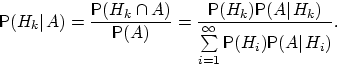
Формула Бернулли.

Закон распределения Бернулли. Случайная величина 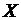, распределенная по закону Бернулли (индикаторная случайная величина), принимает значения: 1 – «успех» или 0 – «неудача» с вероятностям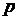и и 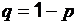соответственно

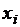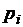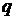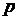Математическое ожидание случайной величины : .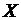

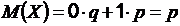Дисперсия: .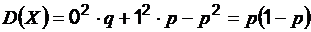

Дискретные случайные величины. Закон распределения. Функция распределения, ее свойства.

Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число (изолированных) значений. Например, можно рассмотреть случайную величину 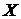– число точек на грани игрального кубика, выпадающее при его подбрасывании.

Законом распределения дискретной случайной величины называется соотношение между ее возможными значениями и их вероятностями (т. е. вероятностями, с которыми случайная величина принимает эти возможные значения).

Функцией распределения (интегральной функцией распределения) случайной величины 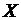называется функция

,

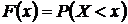определяющая вероятность того, что случайная величина 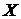примет значение, меньшее .

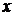Свойства функции распределения:

а) функция распределения принимает значения только из отрезка [0,1]:

0 ≤ F(x) ≤ 1;

б) F(x) – неубывающая функция, т.е. если x₂ > x₁, то F(x₂) > F(x₁) ;

в) F(- ∞ ) = 0; F(+ ∞) = 1;

г) вероятность того, что случайная величина примет значение из

интервала 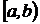(причем 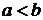), равна:

;

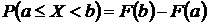д) F(x) непрерывна слева, т. е. F(x) = F(x – 0)

Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек 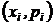, соединенных отрезками