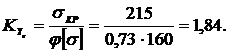Задача 8 – Расчет сжатых стержней на устойчивость

Задание. Стальной стержень длиной l сжимается силой F. Требуется:

1) найти размеры поперечного сечения при допускаемом напряжении на сжатие [σ] = 160 МПа (расчет производить последовательными приближениями, предварительно задавшись коэффициентом φ = 0,5);

2) найти значение критической силы и коэффициент запаса устойчивости.

Данные взять из таблицы 8.

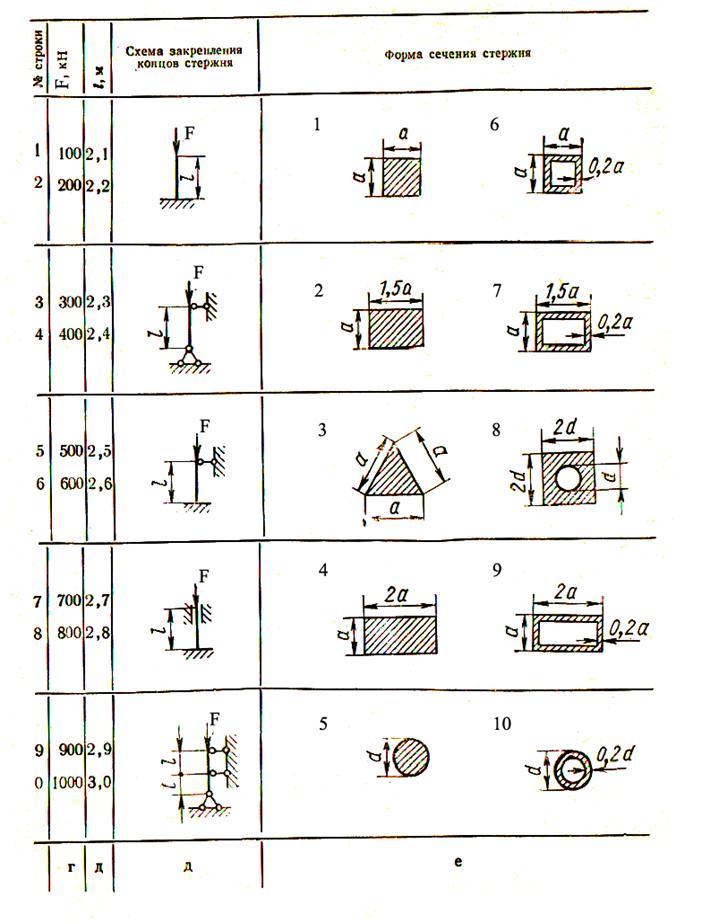
Таблица 6 –Исходные данные к задаче 8

Пример 8. Рассмотрим стальной стержень, представленный на рисунке 31.

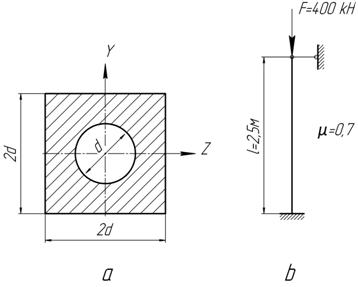
Рисунок 31 – Расчетная схема стержня

Данные для расчета F = 400 кН; 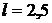м.

Решение

Площадь стержня определим, исходя из условия устойчивости

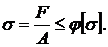
Отсюда

A=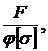

где 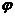– коэффициент уменьшения основного допускаемого напряжения для сжатых стержней.

Расчет приведем последовательными приближениями.

1. Примем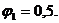

а) Определим площадь поперечного сечения стержня:

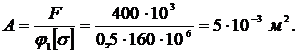
б) Выразим площадь поперечного сечения заданной формы через размер d (рисунок 31а):

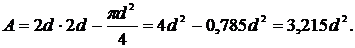
Отсюда определим размер d:

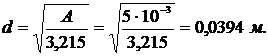
в) Выразим минимальный радиус инерции через размер сечения d:

i_min =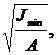

где J_min – минимальный момент инерции поперечного сечения

стержня относительно одной из главных центральных

осей.

В нашем случае

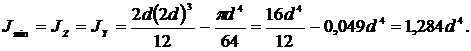
Тогда

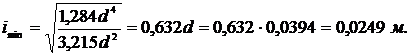
г) Найдем гибкость стержня:

,

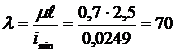где 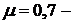коэффициент, учитывающий характер закрепления

концов стержня (коэффициент приведенной длины).

По найденной гибкости стержня 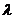определим табличное значение коэффициента 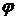[2, 3]:

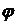_табл = 0,81.

д) Определим расчетное напряжение в стержне пр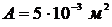и и :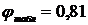

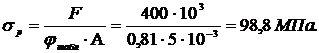
Недонапряжение стержня составит

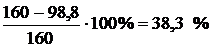
Недогрузка стержня велика, поэтому необходимо сделать перерасчет.

2. Выполним второе приближение, приняв

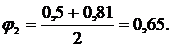
а) Снова определим площадь поперечного сечения стержня:

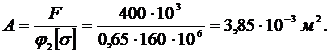
б) Найдем размер d:

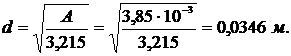
в) Рассчитаем радиус инерции:

.

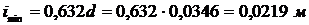г) Определим гибкость:

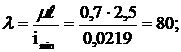
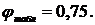
д) Проверим расчетное напряжение в стержне:

.

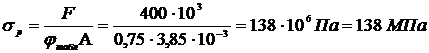Недонапряжение составит

.

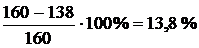Недогрузка велика.

3. Сделаем третье приближение, приняв .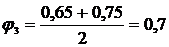

а) Определим площадь:

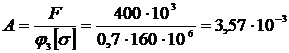м².

б) Тогда, размер 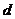равен:

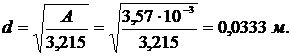
в) Следовательно, радиус инерции

.

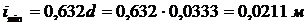г) Затем найдем гибкость стержня:

.

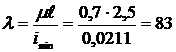Табличное значение коэффициента 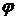определим в этом случае методом интерполирования.

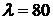
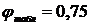При , при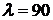

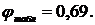
Тогда при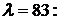

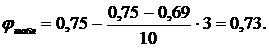
д) Проверим расчетное напряжение

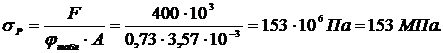
Недонапряжение стержня равно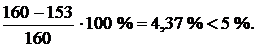

Отклонение напряжения от номинальной величины допускается в инженерных расчетах в пределах 4 – 5 %. Следовательно, третье приближение является окончательным. Необходимый размер сечения 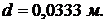Площадь поперечного сечения .

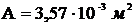4. Определим величину критической силы.

Поскольку гибкость данного стержня по нашим расчетам меньше предельной гибкости для стали Ст. 3 ( 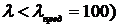, то для определения критического напряжения следует использовать формулу Ясинского:

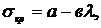
где а и в – эмпирические коэффициенты, зависящие от свойств

материала,

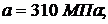
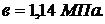
Тогда .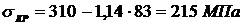

Следовательно, критическая сила

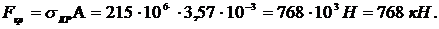
Найдем коэффициент запаса устойчивости