Виды изолированных особых точек

Геометрические понятия

e-окрестностью точки a называется множество 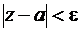(e>0), т.е. открытый круг с центром в точке a.

Областью называется множество точек D на комплексной плоскости, удовлетворяющее условиям:

1) вместе с каждой точкой из D этому множеству принадлежит некоторая e-окрестность этой точки (свойство открытости);

2) любые две точки, принадлежащие D можно соединить непрерывной кривой, состоящей из точек D (свойство связности).

Граничной точкой области D называется точка, не принадлежащая D, если в любой ее e-окрестности существуют точки, принадлежащие D.

Множество всех граничных точек образует границу G области D.

В дальнейшем будем предполагать, что все линии, входящие в границу G, а также все другие кривые и контура, которые будут рассматриваться ниже, являются кусочно-гладкими.

Особый вид границы представляет собой разрез (см. линии g₁ и g₂ на рис. 1.3). Можно считать, что разрез состоит из двух совпадающих участков границы (которые называют берегами разреза), ограничивающих область с разных сторон. Совпадающие (кратные) точки этих участков имеют одинаковые декартовы координаты, но могут иметь разные аргументы.

Если, двигаясь вдоль границы можно достичь любой ее точки (т.е. вся граница является связной), то область называется односвязной. Кроме односвязных областей рассматриваются, области с границами, состоящими из конечного числа связных частей. Число связных частей границы называется порядком связности области. Например, на рис. 1.3 изображена пятисвязная область, состоящая из связных частей: G₀Èg₁ – внешней границы с примыкающим разрезом, G₁ и G₂ – внутренних границ, g₂ – внутреннего изолированного разреза, g₃ – точки-разреза.

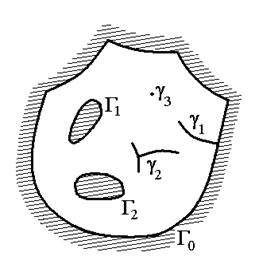
Рис. 1.3.Вид неодносвязной области

1.3. Предел, дифференцируемость и аналитичность функции комплексного переменного

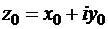Определение. Пусть определена и однозначна в некоторой окрестности точки , (кроме, может быть, самой этой точки). Будем говорить, что существует предел 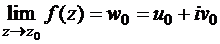, если существуют пределы 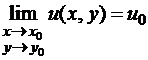, , 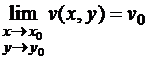как пределы функций двух переменных.

Основные свойства пределов функций действительных переменных остаются справедливыми и для функций комплексного переменного. Так же переносятся на функции комплексного переменного понятие непрерывности и свойства непрерывных функций.

Определение. Пусть определена в некоторой окрестности точки z. Будем говорить, что дифференцируема в точке z, если существует предел

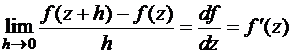(h – комплексное).

Этот предел называют производной в точке z.

Теорема 1. Пусть 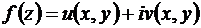определена в некоторой окрестности точки z, причем в z функци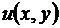и и 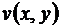дифференцируемы. Тогда для дифференцируемости функции комплексного переменного необходимо и достаточно, чтобы в z имели место равенства 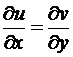, , 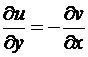которые называют условиями Коши-Римана (или Эйлера-Д'Аламбера).

Для производной 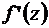справедливы свойства производных функций одного переменного. Производная 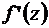выражается через частные производные функци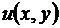й и 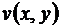следующим образом

.

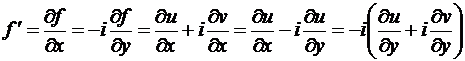Определение. Функция , дифференцируемая в каждой точке области D, называется аналитической (или регулярной, голоморфной) в этой области. Точки, где не существует производная , называются особыми точками функции. В дальнейшем большое значение будут иметь изолированные особые точки (в достаточно малой окрестности которых нет других особых точек). В бесконечно удаленной точке может существовать конечный предел 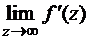. В этом случае f¢(z) имеет в точке z=¥ устранимый разрыв. Положим 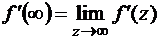. Тем самым, точка z=¥ включается в область D аналитичности функции f(z).

В частности, можно показать, что аналитическими (как правило, на всей плоскости, за исключением некоторых множеств изолированных особых точек) являются элементарные функции 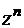, , 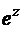, 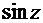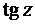и т.д.

1.4. Интегрирование функций комплексного переменного

Пусть C – некоторая кривая в области D, – кусочно-непрерывна и ограничена в D. Тогда по определению

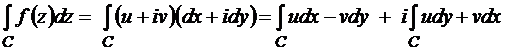
Тем самым интегрирование функции комплексного переменного сводится к вычислению криволинейных интегралов от действительных функций действительного переменного.

Теорема 2 (Коши). Если функция аналитична в односвязной области D, то для любой пары точек A, B и всех кривых C, соединяющих эти точки и лежащих в этой области, интеграл 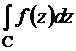имеет одно и то же значение.

В связи с этим вместо 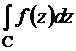можно записывать .

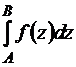Для интеграла от функции комплексного переменного справедливы свойства интеграла от функции одного действительного переменного.

Вследствие теоремы Коши для замкнутой кривой C интеграл

.

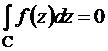Справедлива обратная теорема (Г. Морера). Если функция непрерывна в односвязной области D и интеграл 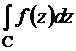по любому замкнутому контуру, лежащему в D, равен 0, то аналитична в этой области.

Эта теорема приводит к важному следствию. Если функция аналитична в односвязной области D, граница которой содержит разрез g₁, и непрерывна в DÈg₁, то аналитична в DÈg₁.

Обобщение теоремы Коши. Если аналитична в односвязной ограниченной области D и непрерывна в замкнутой области 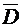, то интеграл от , взятый вдоль границы Γ этой области, равен нулю.

Рассмотрим теперь в качестве примера интеграл от функции 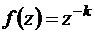, (k>0 – целое) по двусвязной области, представляющей собой круг 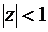с точечным разрезом O ( 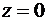) по некоторой кривой C, охватывающей точку 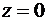(не проходящей через нее).

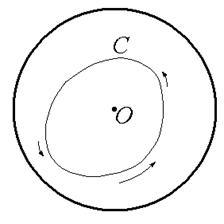
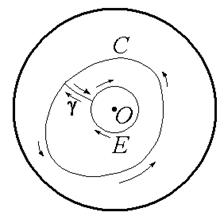
а б

Рис. 1.4.Интегрирование в двусвязной области

Отметим, что если контур интегрирования C не охватывает точку 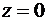, то функция 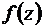, аналитична в односвязной области, заключенной внутри контура C, а вследствие обобщенной теоремы Коши, интеграл от данной функции по границе C равен нулю.

Выберем окружность E достаточно малого радиуса e с центром в точке O так, чтобы она целиком находилась внутри C. Проведем разрез g, соединяющий контур C с окружностью E. Тогда интеграл по замкнутому контуру 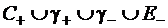, не охватывающему точку O

,

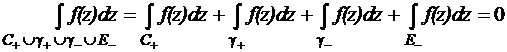где индексы «+» и «–» обозначают направление прохождения контура. Тогда

, ,

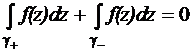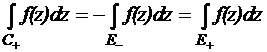т.е. интеграл по замкнутому контуру равен константе, не зависящей от конкретной формы контура (если он охватывает точку O один раз).

Значение этой константы вычислим с помощью замены переменного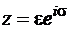

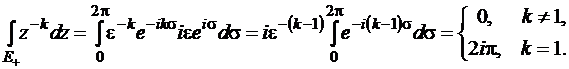
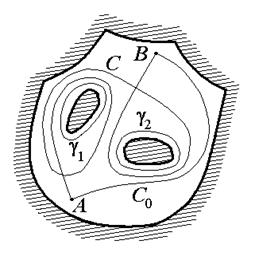
Рассмотрим неодносвязную область (рис. 1.4,а). Обозначим 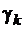– любой контур, охватывающий один раз одну связную часть границы.

а б

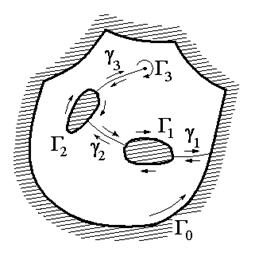
Рис. 1.5.Интегрирование в неодносвязной области

Интегралы 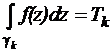называются циклическими постоянными (будем считать, что обход контура 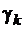осуществляется в положительном направлении – против часовой стрелки).

Допустим, что C, C₀ – различные контуры интегрирования, охватывающие часть внутренних границ, соединяющие точки A и B. Тогда интеграл

,

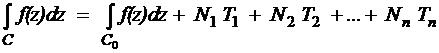где 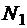, …, 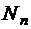– целые числа, равные количеству обходов одной связной части границы в положительном направлении. При обходе в отрицательном направлении числа N_k имеют отрицательные значения. В рассмотренном на рис. 1.5 примере N₁=N₂=-1.

С помощью разрезов любую многосвязную область можно сделать односвязной (см., например, рис. 1.4,б, разрезы g₁, g₂, g₃). Тогда для нее будет справедлива теорема Коши. Но заметим, что интегралы по каждому разрезу встречаются ровно два раза, они равны по модулю и имеют противоположные знаки, так как каждый разрез проходится два раза в противоположном направлении (рис. 1.4,б). Поэтому интегралы по разрезам взаимно уничтожаются.

Тем самым, теорему Коши можно обобщить на многосвязные области. Интеграл от аналитической функции равен нулю, если интегрировать вдоль всей границы многосвязной области D, но при этом направление обхода каждой связной части границы должно выбираться так, чтобы D всегда оставалась слева (или всегда справа). Отметим, что если связная часть границы, представляет собой изолированную точку, то при обходе интегрировать приходится по окружности малого радиуса e и определять предел при e®0.

1.5. Формулы Коши, Шварца и Келдыша-Седова

Пусть аналитична в n-связной области D и непрерывна в 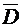. Тогда для любой внутренней точки z этой области имеет место формула Коши

,

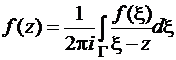где G – граница области, проходимая так, что область D остается всегда слева.

Таким образом, аналитическая функция полностью определяется своими граничными значениями. Более того, задания только одной действительной (или мнимой) части на границе достаточно для определения внутри области (с точностью до аддитивной постоянной).

Это свойство аналитических функций является ключевым для формулировки краевых задач.

Например, если область D представляет собой единичный круг 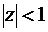(а граница – окружность 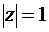) и на всей границе задана только действительная часть 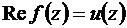, решение задачи может быть получено с точностью до постоянного мнимого слагаемого 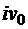по формуле Шварца

.

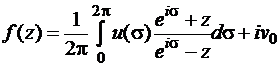Если область D – верхняя полуплоскость 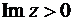(а граница – действительная ось 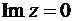), то формула Шварца принимает вид

.

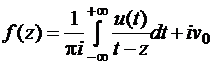Для области D в виде полосы 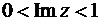формула Шварца имеет вид

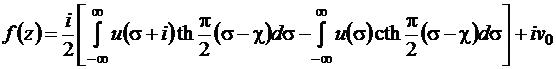
(предполагается, что интегралы в этих выражениях существуют).

Для приложений полезна следующая смешанная краевая задача.

На границе G односвязной области D заданы точки 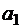, , 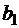, ,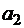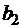…, , 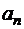, 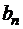расположенные так, что при обходе границы в направлении от 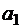к 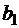и далее к 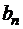область остается слева. Требуется найти функцию , аналитическую в D, действительная часть которой принимает заданные значения на дугах 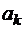, , 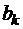а мнимая часть – заданные значения на дугах , ( ; ).

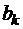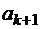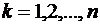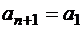При решении задач область D обычно конформно отображают (понятие конформного отображения дано в п. 1.7) на верхнюю полуплоскость или круг или на другую область достаточно простой конфигурации.

Теорема 3 (М. В. Келдыш, Л. И. Седов). Смешанная задача для верхней полуплоскости имеет единственное решение , удовлетворяющее следующим условиям:

1. ограничена вблизи всех точек ;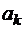

2. вблизи всех точек b_k ограничен интеграл ;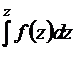

3. имеет конечный предел 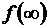при 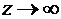, который для простоты полагается действительным.

В этом случае можно получить по формуле

,

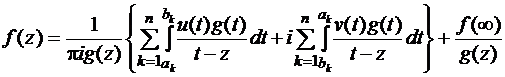которую принято называть формулой Келдыша-Седова. Здесь обозначено

.

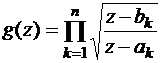Заметим, что интегралы в приведенных выше формулах существуют в обычном смысле, если точка z не лежит на границе L области D. Если 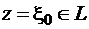, то существуют предельные значения интегралов (в смысле главного значения):

, .

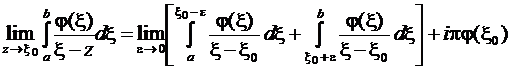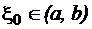Высшие производные

Исходя из формулы Коши, прямым дифференцированием под знаком интеграла получим

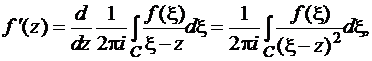
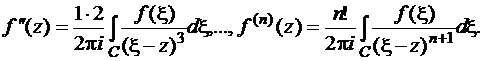
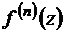Вследствие этого аналитическая в области D и непрерывная на ее границе функция имеет производную любого порядка, которая является аналитической в D функцией.

Теорема 4 (Лиувилль). Если аналитична в полной комплексной плоскости (включая бесконечно удаленную точку), то она постоянна.

Теорема Лиувилля позволяет решать многие задачи методом выделения особенностей.

1.6. Представление функций комплексного переменного рядами

Теорема 5 (Коши). В любом открытом круге с центром в точке a, в котором функция аналитична, она представима своим рядом Тейлора

.

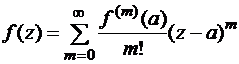Во всякой замкнутой области, принадлежащей этому кругу, ряд Тейлора сходится равномерно.

Ряд Лорана

Рассмотрим функцию, аналитическую в кольце ,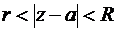
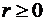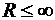, . В этом случае можно построить разложение вида

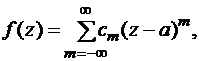где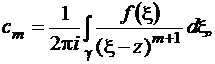

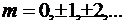
Теорема 6 (Лоран).В любом кольце K: 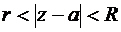, в котором аналитична , эта функция может быть представлена своим рядом Лорана, равномерно сходящимся в любой замкнутой области, принадлежащей кольцу K.

Дробно-линейное отображение

Функция, осуществляющая данное отображение, имеет вид 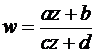, где a, b, c, d – комплексные постоянные (поскольку рассматриваются функции, отличные от константы, то дробь должна быть несократимой, т.е. ).

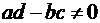Отметим, что , .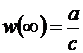

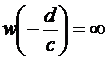Теорема 9. Если функция всюду однолистна и аналитична в полной плоскости z, кроме точки C, то она дробно-линейна.

Отображение многоугольников

Теорема 11. (Шварц, Кристоффель). Если функция реализует конформное отображение верхней полуплоскости 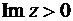на внутренность многоугольника 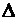с углами 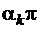(k = 1, 2, …, n) при вершинах, то представима интегралом

,

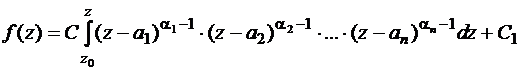где 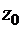, C, C₁ – некоторые постоянные, 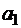, , 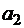..., 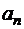– прообразы вершин многоугольника на плоскости z.

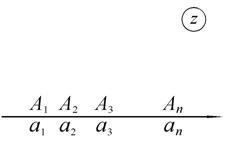
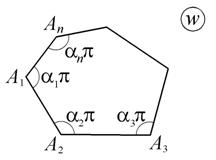
Рис. 1.16.Отображение верхней полуплоскости на многоугольник

Замечание 1. Многоугольником здесь считается фигура, ограниченная отрезками прямых, лучами и прямыми и может содержать вершины, удаленные на бесконечность. При этом угол при бесконечно удаленной вершине определяется как угол между прямыми в точке пересечения продолжений сторон, взятый со знаком минус. Если прямые параллельны, то угол может быть равен 0 или -kp. Угол можно определить, построив дугу окружности (бесконечно) большого радиуса внутри области между лучами, образующими угол.

Замечание 2. Если прообразом одной из вершин является бесконечно удаленная точка плоскости z, то соответствующий ей множитель в подынтегральной функции исключается.

Замечание 3. Для приложений важен случа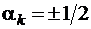й или 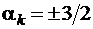. В случае одного или двух таких значений угловых коэффициентов 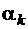(и произвольного числа целых 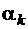) выражается через элементарные функции, для трех или четырех полуцелых 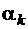интеграл Шварца-Кристоффеля сводится к эллиптическим интегралам [3].

¹ Порядок изложения материала в данном разделе, за небольшим исключением, совпадает с принятым в работе [1].

Геометрические понятия

e-окрестностью точки a называется множество 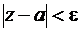(e>0), т.е. открытый круг с центром в точке a.

Областью называется множество точек D на комплексной плоскости, удовлетворяющее условиям:

1) вместе с каждой точкой из D этому множеству принадлежит некоторая e-окрестность этой точки (свойство открытости);

2) любые две точки, принадлежащие D можно соединить непрерывной кривой, состоящей из точек D (свойство связности).

Граничной точкой области D называется точка, не принадлежащая D, если в любой ее e-окрестности существуют точки, принадлежащие D.

Множество всех граничных точек образует границу G области D.

В дальнейшем будем предполагать, что все линии, входящие в границу G, а также все другие кривые и контура, которые будут рассматриваться ниже, являются кусочно-гладкими.

Особый вид границы представляет собой разрез (см. линии g₁ и g₂ на рис. 1.3). Можно считать, что разрез состоит из двух совпадающих участков границы (которые называют берегами разреза), ограничивающих область с разных сторон. Совпадающие (кратные) точки этих участков имеют одинаковые декартовы координаты, но могут иметь разные аргументы.

Если, двигаясь вдоль границы можно достичь любой ее точки (т.е. вся граница является связной), то область называется односвязной. Кроме односвязных областей рассматриваются, области с границами, состоящими из конечного числа связных частей. Число связных частей границы называется порядком связности области. Например, на рис. 1.3 изображена пятисвязная область, состоящая из связных частей: G₀Èg₁ – внешней границы с примыкающим разрезом, G₁ и G₂ – внутренних границ, g₂ – внутреннего изолированного разреза, g₃ – точки-разреза.

Рис. 1.3.Вид неодносвязной области

1.3. Предел, дифференцируемость и аналитичность функции комплексного переменного

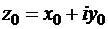Определение. Пусть определена и однозначна в некоторой окрестности точки , (кроме, может быть, самой этой точки). Будем говорить, что существует предел 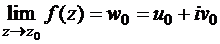, если существуют пределы 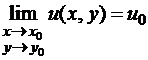, , 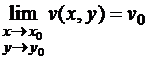как пределы функций двух переменных.

Основные свойства пределов функций действительных переменных остаются справедливыми и для функций комплексного переменного. Так же переносятся на функции комплексного переменного понятие непрерывности и свойства непрерывных функций.

Определение. Пусть определена в некоторой окрестности точки z. Будем говорить, что дифференцируема в точке z, если существует предел

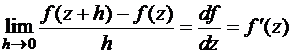(h – комплексное).

Этот предел называют производной в точке z.

Теорема 1. Пусть 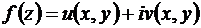определена в некоторой окрестности точки z, причем в z функци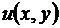и и 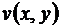дифференцируемы. Тогда для дифференцируемости функции комплексного переменного необходимо и достаточно, чтобы в z имели место равенства 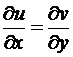, , 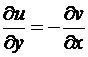которые называют условиями Коши-Римана (или Эйлера-Д'Аламбера).

Для производной 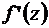справедливы свойства производных функций одного переменного. Производная 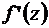выражается через частные производные функци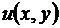й и 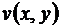следующим образом

.

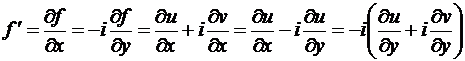Определение. Функция , дифференцируемая в каждой точке области D, называется аналитической (или регулярной, голоморфной) в этой области. Точки, где не существует производная , называются особыми точками функции. В дальнейшем большое значение будут иметь изолированные особые точки (в достаточно малой окрестности которых нет других особых точек). В бесконечно удаленной точке может существовать конечный предел 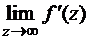. В этом случае f¢(z) имеет в точке z=¥ устранимый разрыв. Положим 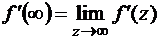. Тем самым, точка z=¥ включается в область D аналитичности функции f(z).

В частности, можно показать, что аналитическими (как правило, на всей плоскости, за исключением некоторых множеств изолированных особых точек) являются элементарные функции 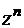, , 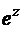, 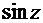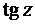и т.д.

1.4. Интегрирование функций комплексного переменного

Пусть C – некоторая кривая в области D, – кусочно-непрерывна и ограничена в D. Тогда по определению

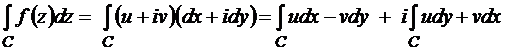
Тем самым интегрирование функции комплексного переменного сводится к вычислению криволинейных интегралов от действительных функций действительного переменного.

Теорема 2 (Коши). Если функция аналитична в односвязной области D, то для любой пары точек A, B и всех кривых C, соединяющих эти точки и лежащих в этой области, интеграл 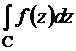имеет одно и то же значение.

В связи с этим вместо 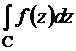можно записывать .

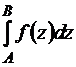Для интеграла от функции комплексного переменного справедливы свойства интеграла от функции одного действительного переменного.

Вследствие теоремы Коши для замкнутой кривой C интеграл

.

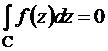Справедлива обратная теорема (Г. Морера). Если функция непрерывна в односвязной области D и интеграл 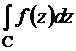по любому замкнутому контуру, лежащему в D, равен 0, то аналитична в этой области.

Эта теорема приводит к важному следствию. Если функция аналитична в односвязной области D, граница которой содержит разрез g₁, и непрерывна в DÈg₁, то аналитична в DÈg₁.

Обобщение теоремы Коши. Если аналитична в односвязной ограниченной области D и непрерывна в замкнутой области 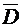, то интеграл от , взятый вдоль границы Γ этой области, равен нулю.

Рассмотрим теперь в качестве примера интеграл от функции 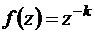, (k>0 – целое) по двусвязной области, представляющей собой круг 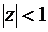с точечным разрезом O ( 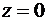) по некоторой кривой C, охватывающей точку 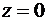(не проходящей через нее).

а б

Рис. 1.4.Интегрирование в двусвязной области

Отметим, что если контур интегрирования C не охватывает точку 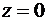, то функция 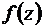, аналитична в односвязной области, заключенной внутри контура C, а вследствие обобщенной теоремы Коши, интеграл от данной функции по границе C равен нулю.

Выберем окружность E достаточно малого радиуса e с центром в точке O так, чтобы она целиком находилась внутри C. Проведем разрез g, соединяющий контур C с окружностью E. Тогда интеграл по замкнутому контуру 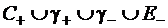, не охватывающему точку O

,

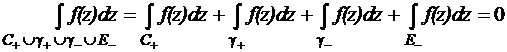где индексы «+» и «–» обозначают направление прохождения контура. Тогда

, ,

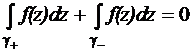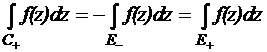т.е. интеграл по замкнутому контуру равен константе, не зависящей от конкретной формы контура (если он охватывает точку O один раз).

Значение этой константы вычислим с помощью замены переменного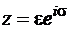

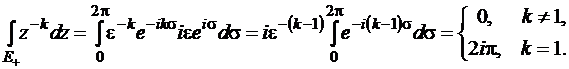
Рассмотрим неодносвязную область (рис. 1.4,а). Обозначим 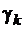– любой контур, охватывающий один раз одну связную часть границы.

а б

Рис. 1.5.Интегрирование в неодносвязной области

Интегралы 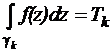называются циклическими постоянными (будем считать, что обход контура 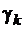осуществляется в положительном направлении – против часовой стрелки).

Допустим, что C, C₀ – различные контуры интегрирования, охватывающие часть внутренних границ, соединяющие точки A и B. Тогда интеграл

,

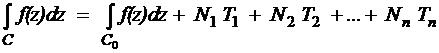где 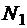, …, 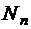– целые числа, равные количеству обходов одной связной части границы в положительном направлении. При обходе в отрицательном направлении числа N_k имеют отрицательные значения. В рассмотренном на рис. 1.5 примере N₁=N₂=-1.

С помощью разрезов любую многосвязную область можно сделать односвязной (см., например, рис. 1.4,б, разрезы g₁, g₂, g₃). Тогда для нее будет справедлива теорема Коши. Но заметим, что интегралы по каждому разрезу встречаются ровно два раза, они равны по модулю и имеют противоположные знаки, так как каждый разрез проходится два раза в противоположном направлении (рис. 1.4,б). Поэтому интегралы по разрезам взаимно уничтожаются.

Тем самым, теорему Коши можно обобщить на многосвязные области. Интеграл от аналитической функции равен нулю, если интегрировать вдоль всей границы многосвязной области D, но при этом направление обхода каждой связной части границы должно выбираться так, чтобы D всегда оставалась слева (или всегда справа). Отметим, что если связная часть границы, представляет собой изолированную точку, то при обходе интегрировать приходится по окружности малого радиуса e и определять предел при e®0.

1.5. Формулы Коши, Шварца и Келдыша-Седова

Пусть аналитична в n-связной области D и непрерывна в 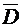. Тогда для любой внутренней точки z этой области имеет место формула Коши

,

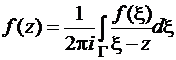где G – граница области, проходимая так, что область D остается всегда слева.

Таким образом, аналитическая функция полностью определяется своими граничными значениями. Более того, задания только одной действительной (или мнимой) части на границе достаточно для определения внутри области (с точностью до аддитивной постоянной).

Это свойство аналитических функций является ключевым для формулировки краевых задач.

Например, если область D представляет собой единичный круг 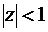(а граница – окружность 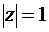) и на всей границе задана только действительная часть 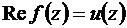, решение задачи может быть получено с точностью до постоянного мнимого слагаемого 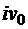по формуле Шварца

.

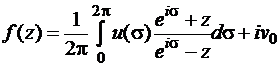Если область D – верхняя полуплоскость 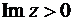(а граница – действительная ось 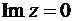), то формула Шварца принимает вид

.

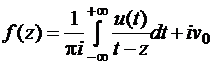Для области D в виде полосы 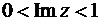формула Шварца имеет вид

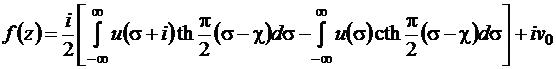
(предполагается, что интегралы в этих выражениях существуют).

Для приложений полезна следующая смешанная краевая задача.

На границе G односвязной области D заданы точки 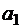, , 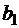, ,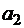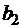…, , 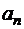, 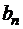расположенные так, что при обходе границы в направлении от 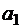к 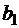и далее к 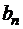область остается слева. Требуется найти функцию , аналитическую в D, действительная часть которой принимает заданные значения на дугах 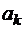, , 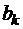а мнимая часть – заданные значения на дугах , ( ; ).

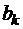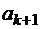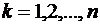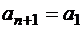При решении задач область D обычно конформно отображают (понятие конформного отображения дано в п. 1.7) на верхнюю полуплоскость или круг или на другую область достаточно простой конфигурации.

Теорема 3 (М. В. Келдыш, Л. И. Седов). Смешанная задача для верхней полуплоскости им