Особая примета» комбинаторных задач
Е. А. Попова
С. А. Раковская
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Практикум
для студентов специальности 080105.65 «Финансы и кредит»,
080502.65 «Экономика и управление на предприятии (в торговле)»,
260501.65 «Технология продуктов общественного питания»,
080401.65 «Товароведение и экспертиза товаров», 080109.65
«Бухгалтерский учет, анализ и аудит», 080507.65 «Менеджмент
организации», 080111.65 «Маркетинг», 080301.65 «Коммерция»
(торговое дело) и направления 260100.62 «Технология продуктов
общественного питания», 080100.62 «Экономика»,
080500.62 «Менеджмент»,
всех форм обучения
Красноярск 2008
УДК 512.1(076.5)
ББК 22.141я73
П 58
Рецензент
кандидат физико-математических наук Л. А. Слонова
Попова Е. А.
П 58 Элементы комбинаторики : практикум / Е. А. Попова, С. А. Раковская; Краснояр. гос. торг.-экон. ин-т. – Красноярск, 2008. – 44 с.
Практикум содержит более ста задач (с решениями и для самостоятельной работы), в том числе профессионально ориентированные для студентов, обучающимся по специальностям 080105.65 «Финансы и кредит», 080109.65 «Бухгалтерский учет, анализ и аудит», 080502.65 «Экономика и управление на предприятии (в торговле)», 080507.65 «Менеджмент организации», 080111.65 «Маркетинг», 080401.65 «Товароведение и экспертиза товаров», 080301.65 «Коммерция» (торговое дело), 260501.65 «Технология продуктов общественного питания»; направлениям 080100.62 «Экономика», 080500.62 «Менеджмент», 260100.62 «Технология продуктов общественного питания».
Предложенное учебное издание может быть полезно не только студентам, преподавателям математики, но и аспирантам, преподавателям и научным работникам, то есть всем, кто сталкивается в своей практической работе с комбинаторными задачами.
УДК 512.1(076.5)
ББК 22.141я73
© ГОУ ВПО «Красноярский государственный торгово-экономический институт», 2008
© Попова Е. А., Раковская С. А., 2008
ОГЛАВЛЕНИЕ
| ПРЕДИСЛОВИЕ……………………………………………………………… | |
| ВВЕДЕНИЕ…………………………………………………………………… | |
| 1. ОСНОВНЫЕ ПОНЯТИЯ КОМБИНАТОРИКИ ………………………… | |
| 1.1. «Особая примета» комбинаторных задач………….………………... | |
| 1.2. Правила сложения и умножения ………………………………….…. | |
| 1.3. Размещения………………………………………………………….…. | |
| 1.4. Перестановки……………………………………………………….….. | |
| 1.5. Сочетания…………………………….………………………………... | |
| 1.6. Размещения с повторениями…………………………………………. | |
| 1.7. Перестановки с повторениями ..……………………………………... | |
| 1.8. Сочетания с повторениями ………………………………………….. | |
| 2. РЕШЕНИЕ ЗАДАЧ ………………………………………………….…….. | |
| 2.1. Разные задачи…...………………………………………………….….. | |
| 2.2. Профессионально ориентированные задачи …………………….….. | |
| 3. ИСПОЛЬЗОВАНИЕ ЭЛЕМЕНТОВ КОМБИНАТОРНОГО АНАЛИЗА ПРИ РАЗРАБОТКЕ МОЛОЧНО-БЕЛКОВЫХ ДЕСЕРТОВ……………. | |
| 4. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ …………….……. | |
| 4.1. Разные задачи…...……………………………………………………….. | |
| 4.2. Профессионально ориентированные задачи…………………………... | |
| БИБЛИОГРАФИЧЕСКИЙ СПИСОК…..…………………………………… | |
| ПРИЛОЖЕНИЯ…………………………………………………………….… |
ПРЕДИСЛОВИЕ
Данный практикум посвящен изучению темы «Комбинаторика» курса «Теория вероятностей», рекомендуется для очного, заочного, дистанционного образования, а также лицам, получающим второе высшее образование. Предлагаемое учебное издание может быть использовано при традиционной форме проведения практических занятий, а также для самостоятельного изучения данной темы.
Идея данного издания возникла в результате общения авторов с инженерами-технологами, экономистами, менеджерами и специалистами в других областях, которые стремятся использовать аппарат комбинаторного анализа для решения специфических задач.
В данном издании сделана попытка, не углубляясь в дебри математических выкладок, однако сохраняя логическую строгость, ввести читателей в курс основных понятий комбинаторного анализа.
Практикум состоит из четырех разделов:
– основные понятия комбинаторики;
– решение задач;
– использование элементов комбинаторного анализа при разработке молочно-белковых десертов;
– задачи для самостоятельного решения.
В практикуме представлено большое количество примеров с решениями, в том числе профессионально ориентированные, а также задачи для самостоятельного решения.
Для удобства принята двойная нумерация параграфов (сквозная нумерация внутри раздела), а нумерация формул, примеров и рисунков тройная (сквозная нумерация внутри параграфа). В номерах формул первое число соответствует номеру раздела, второе номеру параграфа.
Для дальнейшего ознакомления с комбинаторным анализом заинтересованному читателю рекомендуются книги, включенному в библиографический список.
Цель практикума состоит в освещении возможностей практического применения методов комбинаторного анализа, освоении методики решения типовых и профессионально ориентированных задач.
ВВЕДЕНИЕ
В комбинаторике часто случается, что задача, на первый взгляд кажущаяся пустой головоломкой, получает в дальнейшем применение в самых различных областях практической деятельности.
Н. Я. Виленкин
Иногда приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать, складываются в самые разнообразные комбинации. Раздел математики, называемый комбинаторикой, занят поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае. Термин «комбинаторика» был введен в математический обиход Готфридом Вильгельмом Лейбницем. Возникновение основных понятий и развитие комбинаторного анализа шло параллельно с развитием других разделов математики.
Комбинаторика (от позднелат. сombinо – соединение), то же, что комбинаторный анализ – раздел математики, посвященный решению задач выбора и расположения частей некоторого (обычно конечного) множества в соответствии с заданными правилами.
Комбинаторный анализ является разделом дискретной математики, истоки его уходят в глубокую древность. В настоящее время интерес к нему значительно усилился. Благодаря этому комбинаторный анализ сегодня превратился в достаточно развитую ветвь математики, которая непрерывно разрастается. Это делает трудным четко очертить круг объектов и их свойств, которые принадлежат комбинаторике. Ввиду этого мы начинаем с описания простейших (элементарных) комбинаторных объектов.
Идеи комбинаторного характера получили широкое распространение в некоторых разделах математики: теории вероятностей, теории чисел, алгебре и др.
Результаты комбинаторного анализа могут быть использованы при планировании и анализе научных экспериментов, кодировании сообщений, в линейном и динамическом программировании, в математической экономике и многих других областях науки и техники.
1. ОСНОВНЫЕ ПОНЯТИЯ КОМБИНАТОРИКИ
Размещения
Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из m различных элементов (0 ≤ m ≤ n).
Размещениями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо составом элементов, либо порядком их расположения (либо и тем, и другим).
Например, из одного элемента можно составить лишь одно размещение.
Из двух элементов 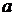 и
и 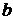 можно составить два размещения по одному элементу:
можно составить два размещения по одному элементу: 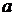 ,
, 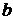 и два размещения по два элемента:
и два размещения по два элемента: 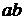 ,
, 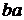 .
.
Из трех элементов 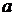 ,
, 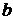 ,
, 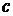 можно составить три размещения по одному элементу:
можно составить три размещения по одному элементу: 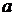 ,
, 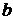 ,
, 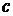 ; шесть размещений по два элемента:
; шесть размещений по два элемента: 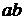 ,
, 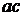 ,
, 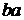 ,
, 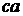 ,
, 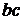 ,
, 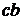 и шесть размещений по три элемента:
и шесть размещений по три элемента: 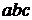 ,
, 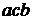 ,
, 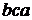 ,
, 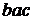 ,
, 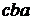 ,
, 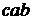 .
.
Все приведенные соединения отличаются друг от друга хотя бы одним элементом или порядком их расположения.
На практике чаше представляет интерес количество размещений, а не их конкретный вид. Число размещений из п элементов по т будем обозначать символом 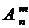 , где 0 ≤ m ≤ n[1].
, где 0 ≤ m ≤ n[1].
Пример 1.3.1. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение. Первую фотографию можно поместить на любую из 12 страниц, т. е. 12 способами, вторую – на любую из оставшихся 11 страниц, т. е. 11 способами. Для размещения третьей фотографии имеется 10 способов, для последней – 9 способов. По правилу умножения четыре фотографии можно разместить на 12 страницах 12 · 11 · 10 · 9 = 11 880 способами.
Найденное число размещений четырех фотографий на 12 страницах газеты – это число. 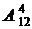 . Действительно, для размещения фотографий следует отобрать 4 различных страницы газеты из 12 имеющихся. Затем необходимо отобранные страницы упорядочить, не обращая внимания на их номера, т. е. определить, на какую страницу поместить первую фотографию, на какую – вторую и т. д.
. Действительно, для размещения фотографий следует отобрать 4 различных страницы газеты из 12 имеющихся. Затем необходимо отобранные страницы упорядочить, не обращая внимания на их номера, т. е. определить, на какую страницу поместить первую фотографию, на какую – вторую и т. д.
Полученная упорядоченная совокупность страниц является размещением из 12 элементов по 4, а число 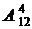 таких размещений является ответом.
таких размещений является ответом.
Таким образом, 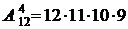 = 11 880.
= 11 880.
Ответ: 11 880.
Число размещений из n элементов по m в каждом вычисляется по формуле[2]
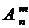 =
= 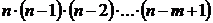 . (1.3.1)
. (1.3.1)
Факториал.Произведение n натуральных чисел от 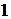 до n обозначается сокращенно n!, то есть 1 · 2 · 3 · 4 · … · (n – 1) · n = n! (читается n факториал).
до n обозначается сокращенно n!, то есть 1 · 2 · 3 · 4 · … · (n – 1) · n = n! (читается n факториал).
Например, 5! = 1 · 2 · 3 · 4 · 5 = 120. По определению 0! = 1.
Используя понятие факториала, формулу ( 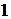 .3.1) можно представить следующим образом:
.3.1) можно представить следующим образом:
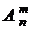 =
= 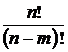 , (1.3.2)
, (1.3.2)
где 0 ≤ m ≤ n.
Очевидно, что 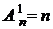 (при m = 1) и
(при m = 1) и 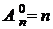 (при m = 0).
(при m = 0).
Пример 1.3.2. Сколько можно записать пятизначных чисел, используя без повторения все десять цифр?
Решение.Так как в любом числе важную роль играет входящих в него цифр, то для ответа на вопрос, очевидно, следует определить число размещений из 10 цифр по 4:
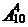 =
= 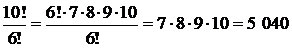 .
.
Не все последовательности из 4 цифр собой четырехзначное число, поскольку среди них есть и те, у которых на 1-м месте находится 0. Найдем число таких последовательностей.
Так как у рассматриваемых последовательностей на 1-м месте уже стоит 0, то следует выбрать еще 3 цифры из оставшихся 9. Найдем число размещений из 9 по 3: 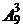 =7 · 8 · 9 = 504. Таким образом, искомое число четырехзначных чисел равно разности
=7 · 8 · 9 = 504. Таким образом, искомое число четырехзначных чисел равно разности 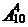 –
– 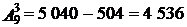 .
.
Ответ: 4 536.
Пример 1.3.3. Расписание одного дня состоит из 6 уроков. Определить число вариантов расписания при выборе из 12 предметов.
Решение. Каждый вариант расписания представляет собой набор 6 дисциплин из 12 вариантов, которые отличаются составом дисциплин, порядком их следования (или и тем, и другим), т. е. является размещением из 12 элементов по 6. Число вариантов расписаний вычисляется по формуле (1.3.2)
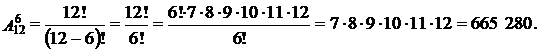
Ответ: 665 280.
Перестановки
Рассмотрим частный случай, когда m = n. Соответствующие этому случаю размещения называют перестановками.
Перестановками из n элементов называются такие соединения, из которых каждое содержит все n элементов, и которые отличаются друг от друга лишь порядком соединения элементов.
Перестановки состоят из одних и тех же элементов, но отличающихся между собой порядком. Перестановки являются частным случаем размещений.
При m = n получаем 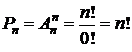
Число перестановок из одного элемента равно 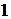 .
.
Число перестановок из двух элементов 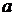 и
и 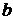 равно двум:
равно двум: 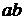 ,
, 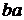 .
.
Число перестановок из трех элементов 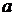 ,
, 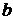 ,
, 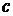 равно шести:
равно шести: 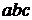 ,
, 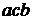 ,
, 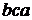 ,
, 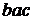 ,
, 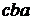 ,
, 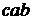 .
.
Число перестановок из n элементов обозначается символом Pn и находится по формуле
Pn = 1 · 2 · 3 · … · (n – 1) · n = n! (1.4.1)
Решение задачи о квартете
Четыре горе-музыканта из басни И. А. Крылова долго пересаживались с места на место. В ходе этого «творческого поиска» Осел внес предложение: «Мы, верно, уж поладим, коль рядом сядем». Определим число возможных перестановок. Здесь n = 4, поэтому способов «усесться чинно в ряд» имеется P4= 4! = 1 · 2 · 3 · 4 = 24.
Для решения некоторых задач приходится применять идею перестановок с поправками. Предположим, что главным влияющим на качество игры фактором являются соседи каждого музыканта (не важно, кто из них справа, а кто слева). При таком условии перестановка «Мартышка, Осел, Козел, Мишка» эквивалентна зеркально-симметричной «Мишка, Козел, Осел, Мартышка». Понятно, что в этом случае все P4 вариантов разбиваются на пары равнозначных перестановок. Если из каждой пары оставить по одной перестановке, то общее число различающихся вариантов будет 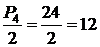 .
.
Предположим, что музыканты сели не в ряд, а по кругу. В этом случае в каждом из вариантов пронумеруем всех участников по часовой стрелке, начиная, например с Мартышки. В различных перестановках каждый музыкант, конечно, должен иметь разные номера. Только у Мартышки будет постоянный номер 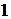 . Значит, осталось пронумеровать различными способами только троих. Поэтому здесь число возможных перестановок P3 = 3! = 6.
. Значит, осталось пронумеровать различными способами только троих. Поэтому здесь число возможных перестановок P3 = 3! = 6.
Пример 1.4.1.Порядок выступления 8 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т. е. является перестановкой из 8 элементов. Их число определяется по формуле (1.4.1)
P8 = 8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40 320.
Ответ: 40 320.
Пример 1.4.2. Сколькими способами можно расставить десять различных книг на полке, чтобы определенные пять стояли рядом?
Решение. Решим задачу двумя способами.
Способ 1. Будем считать выделенные книги за книгу. Тогда для шести книг существует P6 = 6! = 720 перестановок. Однако пять определенных книг можно переставить между собой P5 = 5! = 120 способами. По правилу умножения имеем P6 · P5 = 720 · 120 = 84 400.
Способ 2. Возможны следующие случаи: первая из пяти книг стоит на 1-м месте, тогда пятая стоит на 5-м месте; первая книга стоит на 2-м месте, а пятая стоит на 6-м, первая стоит на 6-м месте, тогда пятая стоит на последнем 10-м месте. Число таких случаев равно шести. Сами книги могут быть переставлены P5 = 5! = 120 способами. По правилу умножения выделенные шесть книг можно расставить 6 · P5 = 720 способами. Оставшиеся пять книг можно переставить P5 = 5! = 120 способами. Воспользовавшись снова правилом умножения, приходим к тому же результату, который был получен при первом способе решения: P5 · 6 · P5 = P5 · P6 = 120 · 720 = 86 400.
Ответ: 86 400.
Сочетания
В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов в той или иной совокупности. Важно лишь то, какие именно элементы ее составляют.
Если два различных размещения состоят из одинаковых элементов некоторого множества, то они обязательно отличаются порядком входящих в них элементов. Иногда возникает необходимость не учитывать порядок элементов, входящих в размещение. В этом случае все m!размещений, которые состоят из одних и тех же m элементов, считаются неразличимыми.
Предположим, что из чисел 3, 5, 7 необходимо составить различные произведения двух чисел. Таких произведений три, а именно: 3 · 5 = 15; 3 · 7 = 21; 5 · 7 = 35. Произведения вида 3 · 5 и 5 · 3 совпадают, так как положение сомножителей, входящих в произведение, не учитывается. Если требуется из указанных цифр составить двузначные числа, то таких чисел уже шесть. Запишем эти числа: 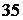 ,
, 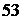 ,
, 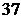 ,
, 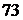 ,
, 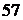 ,
, 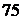 . В этом случае был учтен порядок цифр.
. В этом случае был учтен порядок цифр.
Сочетаниямииз n элементов по m в каждом называют такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга только составом элементов.
Из одного элемента можно составить лишь одно сочетание.
Из двух элементов 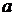 и
и 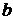 можно составить два сочетания по одному элементу:
можно составить два сочетания по одному элементу: 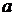 ,
, 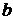 и лишь одно сочетание по два элемента:
и лишь одно сочетание по два элемента: 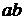 .
.
Из трех элементов 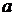 ,
, 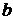 ,
, 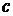 можно составить три сочетания по одному элементу:
можно составить три сочетания по одному элементу: 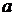 ,
, 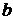 ,
, 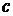 , три сочетания по два элемента:
, три сочетания по два элемента: 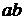 ,
, 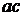 ,
, 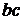 и лишь одно сочетание по три элемента:
и лишь одно сочетание по три элемента: 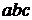 .
.
Все приведенные сочетания в каждом примере отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по m обозначается символом: 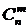 и вычисляется по формулам (1.5.1) и (1.5.2):
и вычисляется по формулам (1.5.1) и (1.5.2):
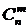
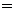
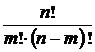 , 0 ≤ m ≤ n; (1.5.1)
, 0 ≤ m ≤ n; (1.5.1)
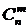
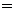
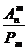 , 0 ≤ m ≤ n. (1.5.2)
, 0 ≤ m ≤ n. (1.5.2)
Свойства сочетаний
1. 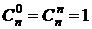 /
/
2. 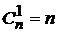 .
.
3. 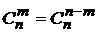 .
.
4. 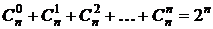 .
.
5. 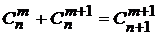 –рекуррентная формула, где 0 < m < n.
–рекуррентная формула, где 0 < m < n.
Пример 1.5.1. Необходимо выбрать в подарок 3 из 10 имеющихся различных книг. Сколькими способами это можно сделать?
Решение. Из смысла задачи следует, что порядок выбора книг не играет роли. Здесь важен их состав. Число возможных способов выбора трех книг в подарок из 10 имеющихся определяется по формуле (1.5.1)
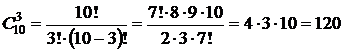 .
.
Ответ: 120.
Пример 1.5.2. В шахматном турнире участвуют 15 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение. Каждая партия играется двумя участниками из 15 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 15 элементов по 2. Их число находим по формуле (1.5.1)
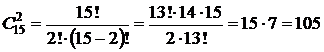 .
.
Ответ: 105.
Пример 1.5.3. Имеется 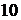 белых и
белых и 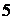 красных шаров. Сколькими способами можно выбрать
красных шаров. Сколькими способами можно выбрать 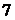 шаров так, чтобы среди них были
шаров так, чтобы среди них были 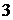 красных?
красных?
Решение. Среди отобранных шаров 4 белых и 3 красных. Белые шары можно выбрать 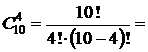
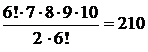 способами. Красные шары можно выбрать
способами. Красные шары можно выбрать 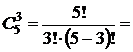
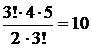 способами. Тогда по правилу произведения искомое число способов равно
способами. Тогда по правилу произведения искомое число способов равно 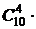
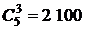 .
.
Ответ: 2 100.
Пример 1. 5. 4. Сколько существует вариантов опроса 12 студентов на одном занятии по английскому языку, если ни один из них не будет подвергнут опросу дважды и на занятии может быть опрошено любое количество учащихся, причем порядок, в котором опрашиваются студенты, безразличен?
Решение. Преподаватель может не опросить ни одного из 12 студентов, что является одним из вариантов. Этому случаю соответствует 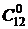 . Преподаватель может опросить только одного из студентов. Таких вариантов
. Преподаватель может опросить только одного из студентов. Таких вариантов 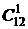 . Если преподаватель будет опрашивать двух студентов, то число вариантов опроса равно
. Если преподаватель будет опрашивать двух студентов, то число вариантов опроса равно 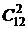 . Для опроса трех студентов существует
. Для опроса трех студентов существует 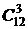 вариантов и т. д. Наконец, могут быть опрошены все студенты данной подгруппы. Число вариантов в этом случае равно
вариантов и т. д. Наконец, могут быть опрошены все студенты данной подгруппы. Число вариантов в этом случае равно 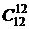 . Тогда по правилу сложения всех возможных вариантов опроса равно
. Тогда по правилу сложения всех возможных вариантов опроса равно
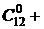
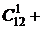
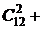
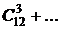
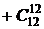 .
.
С другой стороны, для каждого из студентов существует две возможности: он будет опрошен или не опрошен на данном занятии. Другими словами, каждую из 12 операций, заключающихся в том, что каждый студент будет либо опрошен, либо не опрошен, можно выполнить по правилу умножения 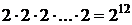 способами, что и следовало ожидать, так как согласно 4-му свойству сочетаний
способами, что и следовало ожидать, так как согласно 4-му свойству сочетаний
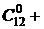
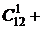
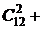
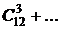
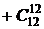
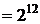 .
.
Ответ: 212.
В размещении учитывается порядок входящих в них элементов, а в сочетаниях – не учитывается. При решении задач это не следует забывать.
Размещения с повторениями
Пусть имеется четыре различных элемента a, b, c, d (в достаточном количестве комплектов) и пусть требуется составить из этих четырех элементов по два элемента размещения с повторениями.
Если бы составлялись размещения без повторения, то все размещения должны были быть различными:
| ab | ba | ac | ca | ad | da | cb | bc | bd | db | dc | cd |
Размещения с повторениями из этих четырех элементов будут следующие:
| aa | ab | ba | ac | ca | ad | da | cb | bc | bd | bb | db | dc | cc | cd | dd |
Таким образом, размещение с повторениями из n элементов по m элементов (при 0 ≤ m ≤ n) может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по m элементов может состоять не только из m различных элементов, но и из m каких угодно и как угодно повторяющихся элементов.
Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.
Число размещений с повторениями из n элементов по m обозначается символом 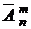 .
.
Число размещений с повторениями определяется по формуле
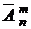
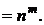 (1.6.1)
(1.6.1)
Решение задачи о паспортах
Определим, сколько может быть паспортов советского образца с различными сериями и номерами, если зафиксировать римские цифры серии. Остаются две русские буквы и шесть арабских цифр. Рассмотрим цифры и буквы отдельно.
Буквы. В русском алфавите 33 буквы. Нам нужно выбрать любые две (они могут быть одинаковыми). Следовательно, имеет место размещение с повторениями, где n = 33 и m = 2.
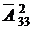
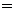 332 = 1 089.
332 = 1 089.
Цифры. Здесь выбирается (с повторениями) m = 6 цифр из n = 10 возможных. Для этого есть 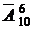
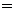
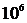 способов.
способов.
Поскольку каждую пару букв можно соединить с любой шестеркой цифр, то возможно существование 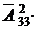
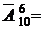 332 · 106 = 1 089 000 000 паспортов, имеющих одни и те же римские цифры серии.
332 · 106 = 1 089 000 000 паспортов, имеющих одни и те же римские цифры серии.
Ответ: 1 089 000 000.
Пример 1.6.1. В гостинице 10 комнат, каждая из которых может разместить четырех человек. Сколько существует вариантов размещения, прибывших четырех гостей?
Решение. Каждый гость из 4 может быть помещен в любую из 10 комнат, поэтому общее число размещений по формуле (1.6.1) равно
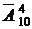
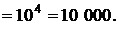
Ответ: 10 000.
Перестановки с повторениями
Пусть имеется пять элементов, среди которых три одинаковых элемента: a, a, a, b, c. Перестановками из этих пяти элементов будут такие соединения, из которых каждое содержит все эти пять элементов и которые будут отличаться друг от друга лишь порядком расположения этих пяти элементов.
Очевидно, что элемент a будет входить в каждое соединение три раза.
Всевозможными перестановками из пяти элементов будут следующие:

Эти перестановки будут перестановками с повторениями потому, что в каждое соединение один и тот же элемент 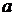 входит три раза, т. е. столько раз, сколько раз он имелся среди данных пяти элементов.
входит три раза, т. е. столько раз, сколько раз он имелся среди данных пяти элементов.
Из приведенных перестановок видно, что их число равно 20. Если же все 5 элементов были бы различными, то число перестановок равнялось бы не 20, а числу 5! = 120.
Предположим теперь, что нам неизвестно число перестановок с повторениями из пяти данных элементов. Обозначим его X. И представим себе, что в группе a, a, a, b, c вместо трех одинаковых элементов a, a, a мы взяли три различных элемента a1, a2, a3. Тогда имеющееся число перестановок 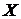 увеличится в 3! раз, т. е. во столько раз, сколько можно сделать перестановок из трех различных элементов. Тогда число всех перестановок будет равно 5! = X : (3!).
увеличится в 3! раз, т. е. во столько раз, сколько можно сделать перестановок из трех различных элементов. Тогда число всех перестановок будет равно 5! = X : (3!).
Отсюда 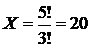 .
.
Нетрудно получить и общую формулу для случая, когда имеется n групп, состоящих соответственно из k1, k2,…, kn неразличимых предметов. Если существует n элементов: a, b, …, c среди которых элемент a повторяется k1 раз, элемент b повторяется k2 раз и т. д., элемент c повторяется kn раз, то число перестановок с повторениями выражается при помощи формулы
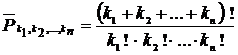 . (1.7.1)
. (1.7.1)
Пример 1.7.1. Сколькими способами можно расставить белые фигуры (короля, ферзя, две ладьи, двух слонов и двух коней) на первой линии шахматной доски (не соблюдая шахматные правила)?
Решение. Всего фигур 8, из них три фигуры по две и две – по одной. По формуле (1.7.1) число перестановок равно 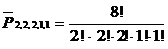 = 5 040.
= 5 040.
Ответ: 5 040.
Пример 1.7.2.Сколько перестановок можно сделать из букв слова «математика»?
Решение. В слове две буквы «м», три буквы «а», две буквы «т», по одной букве «е», «и», «к». Всего 10 букв. По формуле (1.7.1) число перестановок равно
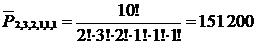 .
.
Ответ: 151 200.
Сочетания с повторениями
Пусть задано 5 различных элементов a, b, c, d, e (в достаточном количестве комплектов) и пусть требуется составить из этих пяти элементов по 3 элемента сочетания с повторениями.
Это значит, что каждое соединение должно содержать три элемента и одно от другого должно отличаться, по крайней мере, одним элементом.
Если бы сочетания составлялись без повторений, то они должны были быть различными:
abc abd abe acd ace ade bcd bce bde cde.
Сочетания же с повторениями по три элемента из заданных пяти элементов будут иметь вид:
| aaa aab aac aad aae abb abc abd abe acb acd ace add ade aee | bbb bbc bbd bbe bce bcd bce bdd bde bee | ccc ccd cce cdd cde cee ddd dde dee eee |
Таким образом, сочетания же с повторениями из n элементов по m элементов (при 0≤ m ≤ n) может содержать любой элемент сколько угодно раз от 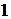 до m включительно, или не содержать его совсем, т. е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но и из m каких угодно и как угодно повторяющихся элементов.
до m включительно, или не содержать его совсем, т. е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но и из m каких угодно и как угодно повторяющихся элементов.
Следует отметить, что если два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.
Число сочетаний с повторениями из n элементов по m будем обозначать символом 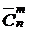 .
.
Существует формула для вычисления числа сочетаний с повторениями:
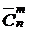
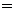
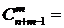
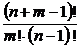 . (1.8.1)
. (1.8.1)
Здесь m может быть и больше n.
Пример 1.8.1. В магазине продается 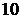 видов тортов. Очередной покупатель выбил чек на три торта. Считая, что любой набор товаров равно-возможен, определить число возможных заказов.
видов тортов. Очередной покупатель выбил чек на три торта. Считая, что любой набор товаров равно-возможен, определить число возможных заказов.
Решение. Число равновозможных заказов по формуле (1.8.1) равно
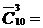
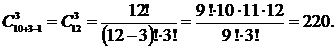
Ответ: 220.
2. РЕШЕНИЕ ЗАДАЧ
Разные задачи
Лучший способ освоения комбинаторики – решение задач. Начинать естественно, надо с простейших. Именно о простых, типовых (и в тоже время важнейших) задачах и пойдет речь.
Пример 2.1.1. В студенческой группе 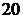 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?
человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?
Решение. Старостой может быть выбран любой из 20 человек, его заместителем – любой из оставшихся 19, а профоргом – любой из 18 студентов, т. е. n1 = 20, n2 = 19, n3 = 18. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно
n1· n2 · n3 = 20 · 19 · 18 = 6 840 способов.
Ответ:6 840.
Пример 2.1.2. Четыре юноши и четыре девушки садятся на 8 расположенных подряд стульев, причем юноши садятся на места с четными номерами, а девушки – на места с нечетными номерами. Сколькими способами это можно сделать?
Решение.Первый юноша может сесть на любое из четырех четных мест, второй – на любое из оставшихся трех мест, третий – на любое из оставшихся двух мест. Последнему юноше предоставляется всего одна возможность. Согласно правилу произведения, юноши могут занять четыре места 4 · 3 · 2 · 1 = 24 способами. Столько же возможностей имеют и девушки.
Таким образом, сог
