Остановимся подробнее на содержании теорем каждой из этих групп.

В практических исследованиях очень важно знать, в каких случаях можно гарантировать, что вероятность события будет или достаточно мала, или как угодно близка к единице.

Под законом больших чисел и понимается совокупность предложений, в которых утверждается, что с вероятностью, как угодно близкой к единице (или нулю), произойдет событие, зависящее от очень большого, неограниченно увеличивающегося числа случайных событий, каждое из которых оказывает на него лишь незначительное влияние.

Точнее, под законом больших чисел понимается совокупность предложений, в которых утверждается, что с вероятностью, как угодно близкой к единице, отклонение средней арифметической достаточно большого числа случайных величин от постоянной величины - средней арифметической их математических ожиданий, не превзойдет заданного как угодно малого числа.

Отдельные, единичные явления, которые мы наблюдаем в природе и в общественной жизни, часто проявляются как случайные (например, регистрируемый смертный случай, пол родившегося ребенка, температура воздуха и др.) вследствие того, что на такие явления действует много факторов, не связанных с существом возникновения или развития явления. Предсказать суммарное действие их на наблюдаемое явление нельзя, и они различно проявляются в единичных явлениях. По результатам одного явления нельзя ничего сказать о закономерностях, присущих многим таким явлениям.

Однако давно было замечено, что средняя арифметическая числовых характеристик некоторых признаков (относительные частоты появления события, результатов измерений и т. д.) при большом числе повторений опыта подвержена очень незначительным колебаниям. В средней как бы проявляется закономерность, присущая существу явлений, в ней взаимно погашается влияние отдельных факторов, которые делали случайными результаты единичных наблюдений.Теоретически объяснить такое поведение средней можно с помощью закона больших чисел. Если будут выполнены некоторые весьма общие условия относительно случайных величин, то устойчивость средней арифметической будет практически достоверным событием. Эти условия и составляют наиболее важное содержание закона больших чисел.

Первым примером действия этого принципа и может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний – факт, установленный в теореме Бернулли (швейцарский математик Якоб Бернулли (1654- 1705)).Теорема Бернулл является одной из простейших форм закона больших чисел и часто используется на практике. Например, частоту встречаемости какого-либо качества респондента в выборке принимают за оценку соответствующей вероятности).

Выдающийся французский математик Симеон Денни Пуассон (1781- 1840) обобщил эту теорему и распространил ее на случай, когда вероятность событий в испытании меняется независимо от результатов предшествующих испытаний. Он же впервые употребил термин «закон больших чисел».

Великий русский математик Пафнутий Львович Чебышев (1821 - 1894) доказал, что закон больших чисел действует в явлениях с любой вариацией и распростаняется также на закономерность средней.

Дальнейшее обобщение теорем закона больших чисел связано с именами А.А.Маркова, С.Н.Бернштейна, А.Я.Хинчина и А.Н.Колмлгорова.

Общая современная постановка задачи, формулировка закона больших чисел, развитие идей и методов доказательства теорем, относящихся к этому закону, принадлежит русским ученым П. Л. Чебышеву, А. А. Маркову и А. М. Ляпунову.

НЕРАВЕНСТВО ЧЕБЫШЕВА

Рассмотрим сначала вспомогательные теоремы: лемму и неравенство Чебышева, с помощью которых легко доказывается закон больших чисел в форме Чебышева.

Лемма (Чебышев).

Если среди значений случайной величины Х нет отрицательных, то вероятность того, что она примет какое-нибудь значение, превосходящее положительное число А , не больше дроби, числитель которой — математическое ожидание случайной величины, а знаменатель - число А:

.

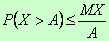Доказательство. Пусть известен закон распределения случайной величины Х:

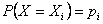(i = 1, 2, ..., ), причем значения случайной величины мы считаем расположенными в возрастающем порядке.

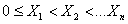
По отношению к числу А значения случайной величины разбиваются на две группы: одни не превосходят А, а другие больше А. Предположим, что к первой группе относятся первые 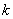значений случайной величины ( ).

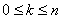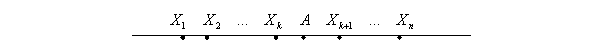
Так как 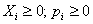, то все члены суммы 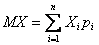неотрицательны. Поэтому, отбрасывая первые 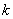слагаемых в выражении 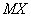получим неравенство:

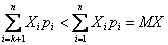
Поскольку

,

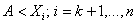то

Далее,

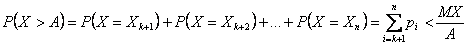
что и требовалось доказать.

Случайные величины могут иметь различные распределения при одинаковых математических ожиданиях. Однако для них лемма Чебышева даст одинаковую оценку вероятности того или иного результата испытания. Этот недостаток леммы связан с ее общностью: добиться лучшей оценки сразу для всех случайных величин невозможно.

Неравенство Чебышева.

Вероятность того, что отклонение случайной величины от ее математического ожидания превзойдет по абсолютной величине положительное число 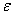, не больше дроби, числитель которой - дисперсия случайной величины, а знаменатель - квадрат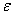

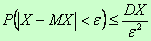
Доказательство. Поскольку 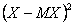случайная величина, которая не принимает отрицательных значений, то применим неравенство 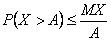из леммы Чебышева для случайной величины 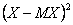при :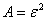

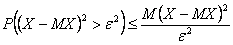
Далее:

что и требовалось доказать.

Следствие. Поскольку

,

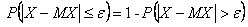и

,

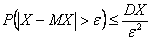то

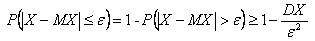
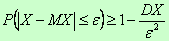- другая форма неравенства Чебышева

Примем без доказательства факт, что лемма и неравенство Чебышева верны и для непрерывных случайных величин.

Неравенство Чебышева лежит в основе качественных и количественных утверждений закона больших чисел. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.

Теорема. (Закон больших чисел в форме Чебышева)

Если дисперсии независимых случайных величин 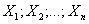ограничены одной константой С, а число их достаточно велико, то как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий не превзойдет по абсолютной величине данного положительного числа 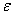, каким бы малым оно ни было:

.

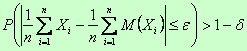Теорему примем без доказательства.

Следствие 1. Если независимые случайные величины имеют одинаковые, равные 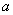, математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число их достаточно велико, то, сколько бы мало на было данное положительное число 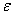, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от 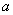не превзойдет по абсолютной величине .

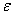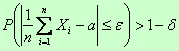
То, что за приближенное значение неизвестной величины принимают среднюю арифметическую результатов достаточно большого числа ее измерений, произведенных в одних и тех же условиях, можно обосновать этой теоремой. Действительно, результаты измерений являются случайными, так как на них действует очень много случайных факторов. Отсутствие систематических ошибок означает, что математические ожидания отдельных результатов измерений одинаковые и равны 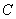. Следовательно, по закону больших чисел средняя арифметическая достаточно большого числа измерений практически будет как угодно мало отличаться от истинного значения искомой величины.

(Напомним, что ошибки называются систематическими, если они искажают результат измерения в одну и ту же сторону по более или менее ясному закону.К ним относятся ошибки, появляющиеся в результате несовершенства инструментов (инструментальные ошибки), вследствие личных особенностей наблюдателя (личные ошибки) и др.)

Следствие 2.(Теорема Бернулли.)

Если вероятность 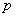наступления события А в каждом из независимых испытаний постоянна, а их число достаточно велико, то сколь угодно близка к единице вероятность того, что частота появления события как угодно мало отличается от вероятности 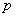его появления:

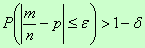
Теорема Бернулли, утверждает, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной.

На практике сравнительно редко встречаются опыты, в которых вероятность появления события в любом опыте неизменна, чаще она разная в разных опытах. К схеме испытаний такого типа относится теорема Пуассона:

Следствие 3.(Теорема Пуассона.)

Если вероятность 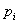появления события 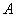в 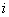-ом испытании не меняется, когда становятся известными результаты предыдущих испытаний, а их число достаточно велико, то сколь угодно близка к единице вероятность того, что частота появления события как угодно мало отличается от средней арифметической вероятностей :

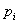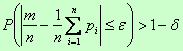
Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.

В заключение заметим, что ни одна из рассмотренных теорем не дает ни точного, ни даже приближенного значения искомой вероятности, а указывается лишь нижняя или верхняя граница ее. Поэтому, если требуется установить точное или хотя бы приближенное значение вероятностей соответствующих событий, возможности этих теорем весьма ограничены.

Приближенные значения вероятностей при больших значениях можно получить только с помощью предельных теорем. В них или на случайные величины налагаются дополнительные ограничения (как это имеет место, например, в теореме Ляпунова), или рассматриваются случайные величины определенного вида (например, в интегральной теореме Муавра—Лапласа).

Теоретическое значение теоремы Чебышева, являющейся весьма общей формулировкой закона больших чисел, велико. Однако если мы будем применять ее при решении вопроса о возможности применить закон больших чисел к последовательности независимых случайных величин, то при утвердительном ответе теорема часто будет требовать, чтобы случайных величин было гораздо больше, чем необходимо для вступления в силу закона больших чисел. Указанный недостаток теоремы Чебышева объясняется общим характером ее. Поэтому желательно иметь теоремы, которые точнее указывали бы нижнюю (или верхнюю) границу искомой вероятности. Их можно получить, если наложить на случайные величины некоторые дополнительные ограничения, которые для встречающихся на практике случайных величин обычно выполняются.