Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
Показательное уравнение вида 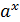 =b (при условии, что числа a и b положительны, где a
=b (при условии, что числа a и b положительны, где a 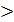 0 ; a
0 ; a 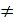 0 и b
0 и b 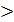 0) имеет решение, которое можно записать:
0) имеет решение, которое можно записать: 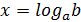
|
Например, 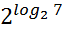 = 7;
= 7; 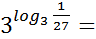
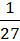 ;
; 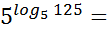 125 и т.д.
125 и т.д.
Определение: Логарифмом положительного числа b по положительному и отличному от единицы основанию a, называется показатель степени x, в которую нужно возвести число a, чтобы получить число b. Таким образом, 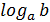 =x
=x
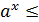 b ; a > 0 ; a < 0 и a
b ; a > 0 ; a < 0 и a 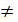 1
1
Операцию нахождение логарифма называют логарифмированием. Эта операция является обратной по отношению к операции возведение в степень соответствующим основаниям.
Возведение в степеньЛогарифмирование
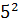 =25
=25 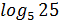 =2
=2
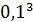 =0,001
=0,001 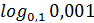 =3
=3
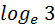 =ln3 =ln3 |
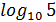 пишут lg 5. Если в основании логарифма стоит число a = e
пишут lg 5. Если в основании логарифма стоит число a = e 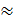 2,71828… e
2,71828… e 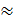 2,7, то такой логарифм называется натуральным и обозначается символом:
2,7, то такой логарифм называется натуральным и обозначается символом: 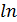 (читается натуральный логарифм), т.е. вместо записи логарифм трёх по основанию e пишут
(читается натуральный логарифм), т.е. вместо записи логарифм трёх по основанию e пишут 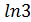
Особо выделим 3 формулы:
1) 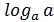 =1 (
=1 ( 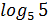 =1)
=1)
2) 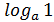 =0 (
=0 ( 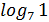 =0)
=0)
3) 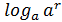 =r (
=r ( 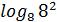 =2)
=2)
Свойства логарифмов.
Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов. Впрочем, два свойства доказательства не требуют, они представляют собой запись на математическом языке определения логарифма как показателя степени. Мы ими уже пользовались:
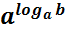 = b = b |
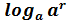 = r = r |
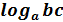 = = 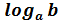 + + 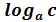 |
Например, 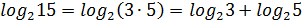 ;
;
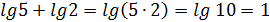 .
.
Доказательство: Введём следующие обозначения.
Подготовка к доказательству Перевод на более Доказательство
(введение новых переменных) простой язык
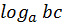 =x
=x 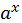 =bc
=bc 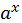 =
= 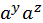
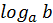 =y
=y 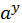 =b
=b 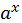 =
= 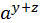
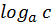 =z
=z 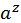 =c x=y+z
=c x=y+z
Доказать x=y+z
Теорема 2.Если a,b,c-положительные числа, причём a 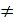 1, то справедливо равенство
1, то справедливо равенство
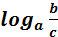 = = 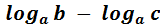 |
Краткая формулировка, которую удобнее использовать на практике: логарифм частного равен разности логарифмов делимого и делителя или логарифм дроби равен разности логарифмов числителя и знаменателя.
Например, 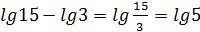
Доказательство:
Подготовка к доказательству Перевод на более Доказательство
(введение новых переменных) простой язык
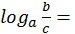 x
x 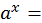

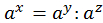
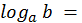 y
y 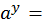 b
b 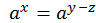
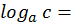 z
z 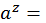 c x
c x 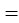 y-z
y-z
Доказать x 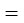 y-z
y-z
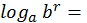 r r 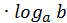 |
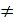 1, то для любого числа r справедливо равенство
1, то для любого числа r справедливо равенство Например, 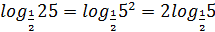
lg 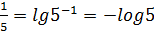
Краткая формулировка, которую удобнее использовать на практике: логарифм степени равен произведению показателя степени на логарифм основания степени.
Доказательство:
Подготовка к доказательству Перевод на более Доказательство
(введение новых переменных) простой язык
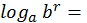 x
x 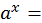
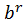
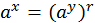
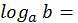 y
y 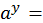 b
b 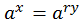
x 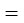 ry
ry
Доказать x=ry
3.Тригонометрические функции числового аргумента(определения, табличные значения).
x 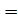 cost cost 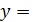 sint sint |
-1 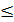 cost cost 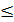 1 -1 1 -1 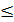 sint sint 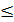 1 1 |
M(x;y)
t
Определение №2: Отношение синуса числа t к косинусу того же числа называется тангенсомчисла t, т.е.tg t 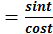
Определение №3: Отношение косинуса t, к синусу t называется котангенсом,т.е. ctg t 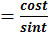
Каждому действительному числу t на числовой окружности можно поставить в соответствии определённое число cost (или sint, или tgt, или ctgt), таким образом, речь идёт о четырёх тригонометрических функциях числового аргумента, где t-любое действительное число.
Табличные значения
Тригонометрических функций
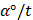 | 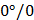 | 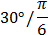 | 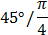 | 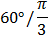 | 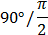 | 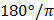 | 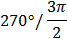 | 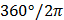 |
| sint | 0 |  | 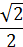 | 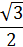 | 1 | 0 | -1 | 0 |
| cost | 1 | 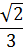 | 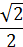 |  | 0 | -1 | 0 | 1 |
| tgt | 0 | 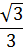 | 1 | 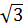 | Не сущ. | 0 | Не сущ. | 0 |
| ctgt | 0 | 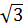 | 1 | 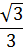 | 0 | Не сущ. | 0 | Не сущ. |

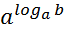 = b
= b