Обратная матрица. Решение систем линейных алгебраических уравнений матричным методом.
Обратная матрица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: 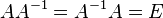
Свойства обратной матрицы:
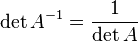 ,где
,где 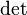 обозначает определитель.
обозначает определитель.
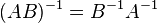 , для любых двух обратимых матриц.
, для любых двух обратимых матриц.
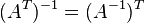 где
где 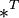 обозначает транспонированную матрицу.
обозначает транспонированную матрицу.
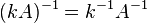 для любого коэффициента
для любого коэффициента  .
.
Если необходимо решить систему линейных уравнений 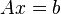 , (b — ненулевой вектор) где
, (b — ненулевой вектор) где 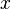 — искомый вектор, и если
— искомый вектор, и если 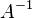 существует, то
существует, то 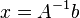 . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
В матричной форме записи эта система уравнений имеет вид 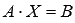 ,
,
где  - основная матрица системы,
- основная матрица системы, 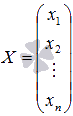 - матрица-столбец неизвестных переменных,
- матрица-столбец неизвестных переменных, 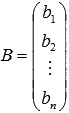 - матрица-столбец свободных членов.
- матрица-столбец свободных членов.
А11=+I…I=… A21=-I…I=… A31=+I…I=…
X=A-1*B
Определение векторов. Действия над ними.
Вектором называется направленный отрезок или упорядоченная пара чисел.
2 вектора называются коллинеарными, если они лежат на одной прямой или на II прямых. Коллинеарные вектора А и В называются сонаправленными, когда их направления совпадают и вектора противоположнонаправлены, если у них направления противоположны. Длиной вектора АВ называется число равное отрезку АВ. Два вектора считаются равными, если длины этих векторов одинаковы и они сонаправлены. Если длина вектора а равна 1, то а называется единичным. А1В1 называется проекцией вектора АВ на прямую l и находится по формуле: А1В1=IABIcosf. Если А имеет координаты Ха и Уа, а В (Хв Ув), то длина вектора АВ находится по формуле: IABI= 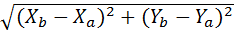 , IaI=
, IaI= 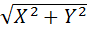
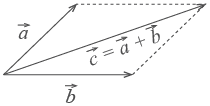
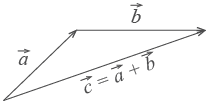
Сложение векторов:
А) правило параллелограмма б) правило треугольника
Вычитание векторов:
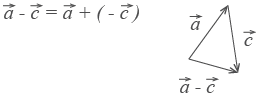
Произведение 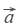 на число k: k
на число k: k 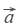 =
=  - необходимое достаточное условие коллинеарности векторов.
- необходимое достаточное условие коллинеарности векторов.
Два вектора IIодной и той же плоскости и лежащие в ней называются компланарными.
Скалярное произведение векторов.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
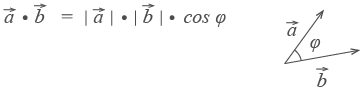
Если векторы перпендикулярны, их скалярное произведение равно нулю.
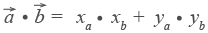
Из формулы для скалярного произведения можно найти угол между векторами:
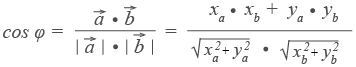
Свойства:
1) 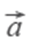
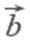 =
= 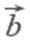
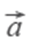
2) K( 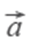
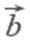 )=(k
)=(k 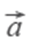 )
) 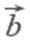 =
= 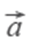 (k
(k 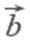 )
)
3) ( 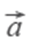
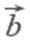 )
) 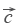 =
= 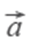 (
( 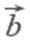
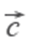 )=
)= 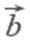 (
( 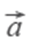
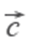 )
)
4) ( 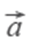 +
+ 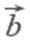 )
) 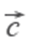 =
= 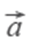
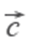 +
+ 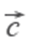
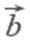
5) 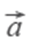
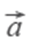 =
= 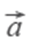 2
2
Векторное произведение векторов.
Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c.
a × b = i j k = i(aybz - azby) - j(axbz - azbx) + k(axby - aybx)
ax ay az
bx by bz
Sпарал = a × b
SΔ = 1 |a × b|
Свойства:
1) a × b = -b × a
2) (k a) × b = a × (k b) = k (a × b)
3) (a + b) × c = a × c + b × c
4) a×a=0
5) Для того чтобы два нулевых вектора были коллинеарны, необходимо и достаточно, чтобы их скалярное произведение было =0
