Определители 2-го и 3-го порядка. Св-ва определителей.

Вопросы к экзамену по математике

1. Определители 2-го и 3-го порядка. Св-ва определителей.

2. Решение систем линейных алгебраических уравнений методом Крамора. Решение систем линейных однородных алгебраических уравнений.

3. Действия над матрицами и их св-ва.

4. Обратная матрица. Решение систем линейных алгебраических уравнений матричным методом.

5. Определение векторов. Действия над ними.

6. Скалярное произведение векторов.

7. Векторное произведение векторов.

8. Смешанное произведение векторов.

9. Уравнение прямой с заданным угловым коэффициентом. Уравнение прямой, проходящей через 2 точки.

10. Общее уравнение прямой на плоскости.

11. Параметрическое и каноническое уравнения прямой на плоскости.

12. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой.

13. Уравнение плоскости в пространстве. Взаимное расположение прямых в пространстве.

14. Взаимное расположение прямой и плоскости в пространстве.

15. Взаимное расположение плоскостей в пространстве.

16. Предел ф-ции. Св-ва пределов.

17. Бесконечно малые ф-ции и их св-ва.

18. Первый замечательный предел. Второй замечательный предел.

19. Сравнение бесконечно малых функций. Таблица эквивалентности.

20. Общее определение производной.

21. Геометрический смысл производной.

22. Связь между дифференцируемостью и непрерывностью ф-ции.

23. Основные правила дифференцирования. Таблица производных.

24. Логарифмическое дифференцирование.

25. Производная сложной ф-ции.

26. Производная неявной ф-ции.

27. Дифференциал ф-ции, св-ва. Его геометрический смысл.

28. Правило Лопиталя.

29. Необходимое и достаточные условия локального экстремума ф-ции одной переменной.

30. Асимптоты графика ф-ции.

31. Исследование ф-ции на выпуклость и вогнутость. Точки перегиба.

32. Первообразная и неопределённый интеграл. Св-ва неопределённого интеграла.

33. Таблица интегралов.

34. Правила интегрирования.

35. Непосредственное интегрирование.

36. Интегрирование методом замены переменной.

37. Интегрирование по частям.

38. Интегрирование простейших рациональных дробей.

39. Интегрирование некоторых классов тригонометрических ф-ций.

40. Основные св-ва определённого интеграла.

41. Формула Ньютона-Лейбница.

42. Замена переменной в определённом интеграле.

43. Интегрирование по частям определённого интеграла.

44. Приложение определённого интеграла.

45. Комплексные числа.

Решение систем линейных алгебраических уравнений методом Крамора.

Действия над матрицами и их св-ва.

Произведением матрицы A=(aij) на число α называется такая матрица B=(bij),элементы которой равны произведениям соответствующих элементов матрицы A на число α, т.е. bij= α·aij Обозначают: α·A

Суммой двух матриц A=(aij) и B=(bij)одинакового размера, называется такая матрица C=(cij), элементы которой равны суммам соответствующих элементов матриц A и B, т.е. cij= aij+ bij.

Обозначают: A+B

Свойства линейных операции над матрицами

1) A + B = B + A (коммутативность сложения матриц);

2) (A + B) + C = A + (B + C) (ассоциативность сложения матриц);

3) A + O = A;

4) A + (–A) = O;

5) α⋅ (βA) = (α⋅β)A (ассоциативность относительно умножения

чисел);

6) (α + β)A = αA + βA (дистрибутивность умножения на матрицу

относительно сложения чисел);

7) α(A + B) = αA + αB (дистрибутивность умножения на число

относительно сложения матриц);

8) 1 ⋅ A = A.

3. Нелинейные операции над матрицами

1) Умножение двух матриц;

2) Транспонирование матрицы.

Произведением матрицы-строки A на матрицу-столбец B называется число c, равное сумме произведений их соответствующих элементов, т.е. c = a11 · b11 + a12 · b21 + a13 · b31 + …+ a1n · bn1 .

Произведением матрицы A на матрицу B называется матрица C =(cij) размера m × k такая, что каждый ее элемент cij является произведением i-й строки матрицы A на j-й столбец матрицы B, т.е. cij= ai1 · b1j + ai2 · b2j + ai3 · b3j + …+ ain · bnj.

Обозначают: A·B, AB.

Свойства операции умножения матриц

1) AE = EA = A , AO = OA = O;

2) (AB)C = A(BC) (ассоциативность умножения матриц);

3) (A + B)C = AC + BC ;

4) C(A + B) = CA + CB .

Свойства операции транспонирования матриц

1) (AТ )T = A ;

2) (A + B)T = AT + BT ;

3) (αA)T = αAT ;

4) (A · B)T = BT · AT .

Сравнение бесконечно малых функций. Таблица эквивалентности.

Функция 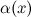называется бесконечно малой при 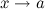(или в точке 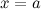), если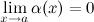

Бесконечно малые функции одного порядка:

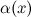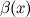Пусть и - две б.м. функции при .

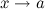Функци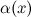и и 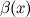называются б.м. одного порядка малости при 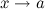, если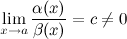

Бесконечно малые функции более низкого и высокого порядков:

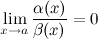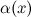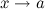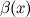1)Если , то является б.м. более высокого порядка при , чем , а 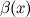- б.м. более низкого порядка по сравнению с 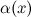: 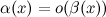при .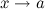

2)Если 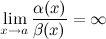, то 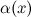- б.м. низшего порядка малости при 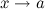по сравнению с .

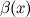3) Если 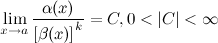, то 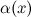называется б.м. порядка 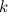по сравнению с 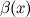при .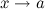

Б.м. функци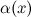и и 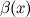называются эквивалентными или равносильными б.м. одного порядка при 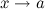, если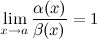

Обозначают: 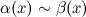при .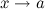

Таблица эквивалентных б.м. функций при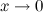

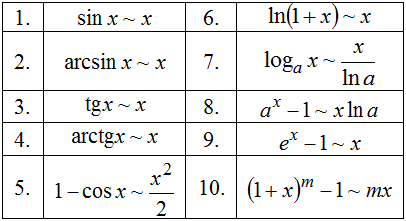
Основные правила дифференцирования. Таблица производных.

Производная сложной ф-ции.

Таблица производных сложных функций

Производная неявной ф-ции.

Если независимая переменная и функция связаны уравнением вида , которое не разрешено относительно , то функция называется неявной функцией переменной .

Всякую явно заданную функцию 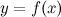можно записать в неявном виде . Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от , а затем из полученного уравнения найти производную .

Правило Лопиталя.

Теорема: (Правило Лопиталя).

Пусть функци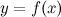и и удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

2) и в этой окрестности;

3) ;

4) существует конечный или бесконечный.

Тогда существует и , причем

Замечание: Правило Лопиталя распространяется на случай неопределенности типа при 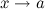. Правило Лопиталя распространяется и на случай . Чтобы убедится в этом, достаточно сделать замену и воспользоваться результатом выше приведенной теоремы. Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми. Хотя правило Лопиталя работает только с неопределенностями и , неопределенности других типов могут быть раскрыты с его помощью, если путем преобразований удастся привести изучаемую неопределенность к указанному типу.

Асимптоты графика ф-ции.

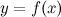Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно или .

Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

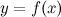Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно .

Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.

Прямая называется наклонной асимптотой графика функции 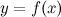, если

Теорема: (условиях существования наклонной асимптоты)

Если для функции 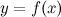существуют пределы и , то функция имеет наклонную асимптоту при .

Замечание: Горизонтальная асимптота является частным случаем наклонной при . Если при нахождении горизонтальной асимптоты получается, что , то функция может иметь наклонную асимптоту. Кривая 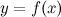может пересекать свою асимптоту, причем неоднократно.

Таблица интегралов.

Правила интегрирования.

Основные правила интегрирования

Интегрирование по частям.

Рассмотрим функции и , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:

Проинтегрировав левую и правую части последнего равенства, получим:

Полученное равенство перепишем в виде:

Эта формула называется формулой интегрирования по частям. С ее помощью интеграл можно свести к нахождению интеграла , который может быть более простым.

Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:

1) ; ;

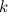Здесь - многочлен степени , - некоторая константа. В данном случае в качестве функции берется многочлен, а в качестве - оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется раз.

2) ; ;

Здесь принимают, что , а в качестве оставшиеся сомножители.

3) ;

В данном случае в качество берется либо экспонента, либо тригонометрическая функция. Единственным условием есть то, что при дальнейшем применении формулы интегрирования по частям в качестве функции берется та же функция, то есть либо экспонента, либо тригонометрическая функция соответственно.

Формула Ньютона-Лейбница.

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на [a, b], то

Приложение определённого интеграла.

Площадь криволинейной трапеции:

Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функции f (x) (рисунок 1), определяется по формуле

Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой

Вычисление длины дуги:

Физическое приложение:

1) Материальная точка движется по некоторой кривой и абсолютная величина скорости v=f(t)

2) F(x)- переменная сила, действующая в направлении Ox на отрезке ав

Комплексные числа.

Основные определения. Операции над комплексными числами

1. Существует элемент i (мнимая единица) такой, что i² = – 1.

2. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b № 0) называют чисто мнимыми.

Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

3. Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.

Любое комплексное число можно изобразить на плоскости х0у в виде точки А с координатами (а,в). Верно и обратное, любую точку с координатами (а,в) можно представить в виде комплексного числа.

Вопросы к экзамену по математике

1. Определители 2-го и 3-го порядка. Св-ва определителей.

2. Решение систем линейных алгебраических уравнений методом Крамора. Решение систем линейных однородных алгебраических уравнений.

3. Действия над матрицами и их св-ва.

4. Обратная матрица. Решение систем линейных алгебраических уравнений матричным методом.

5. Определение векторов. Действия над ними.

6. Скалярное произведение векторов.

7. Векторное произведение векторов.

8. Смешанное произведение векторов.

9. Уравнение прямой с заданным угловым коэффициентом. Уравнение прямой, проходящей через 2 точки.

10. Общее уравнение прямой на плоскости.

11. Параметрическое и каноническое уравнения прямой на плоскости.

12. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой.

13. Уравнение плоскости в пространстве. Взаимное расположение прямых в пространстве.

14. Взаимное расположение прямой и плоскости в пространстве.

15. Взаимное расположение плоскостей в пространстве.

16. Предел ф-ции. Св-ва пределов.

17. Бесконечно малые ф-ции и их св-ва.

18. Первый замечательный предел. Второй замечательный предел.

19. Сравнение бесконечно малых функций. Таблица эквивалентности.

20. Общее определение производной.

21. Геометрический смысл производной.

22. Связь между дифференцируемостью и непрерывностью ф-ции.

23. Основные правила дифференцирования. Таблица производных.

24. Логарифмическое дифференцирование.

25. Производная сложной ф-ции.

26. Производная неявной ф-ции.

27. Дифференциал ф-ции, св-ва. Его геометрический смысл.

28. Правило Лопиталя.

29. Необходимое и достаточные условия локального экстремума ф-ции одной переменной.

30. Асимптоты графика ф-ции.

31. Исследование ф-ции на выпуклость и вогнутость. Точки перегиба.

32. Первообразная и неопределённый интеграл. Св-ва неопределённого интеграла.

33. Таблица интегралов.

34. Правила интегрирования.

35. Непосредственное интегрирование.

36. Интегрирование методом замены переменной.

37. Интегрирование по частям.

38. Интегрирование простейших рациональных дробей.

39. Интегрирование некоторых классов тригонометрических ф-ций.

40. Основные св-ва определённого интеграла.

41. Формула Ньютона-Лейбница.

42. Замена переменной в определённом интеграле.

43. Интегрирование по частям определённого интеграла.

44. Приложение определённого интеграла.

45. Комплексные числа.

Определители 2-го и 3-го порядка. Св-ва определителей.

Определитель – это числовая характеристика матрицы.

Общий знаменатель значений неизвестных легко выражается через элементы матрицы: он равен произведению элементов главной диагонали минус произведение элементов второй диагонали. Это число называется определителем матрицы, причем, как говорят, определителем второго порядка. Произведения a11a22 и a12a21 называются членами определителя второго порядка. Вычисление определителя 2-гопорядка иллюстрируется схемой:

Итак, матрица есть таблица чисел, а определитель – число, соответствующее матрице. Числитель выражений имеет такой же вид, как и знаменатель, т. е. это тоже знаменатель второго порядка. Числитель выражения для x1 есть определитель матрицы, получающейся из матрицы заменой ее первого столбца столбцом из свободных членов системы, а числитель выражения для x2 есть определитель матрицы, получающейся из матрицы такой же заменой ее второго столбца. Таким образом, формулы в новых обозначениях записываются в следующем виде:

Определитель 3-го порядка.

Семь основных свойств определителя 3-го порядка.

Определители третьего порядка (как и определители 2-го порядка) обладают

следующими семью свойствами:

1. определитель не изменится, если строки его матрицы сделать столбцами, а столбцы

строками (определитель не меняется при транспонировании.);

2. при перестановке двух строк определителя он меняет знак;

3. если в определителе имеются две одинаковые строки, то определитель равен нулю;

4. общий множитель определителя строки можно вынести за знак определителя;

5. если элементы одной строки определителя пропорциональны элементам другой, то определитель равен нулю;

6. если к одной строке определителя прибавить другую, умноженную на любое число,

то определитель не изменится.

7. если все элементы какой-то строки или столбца равны 0, то и определитель равен 0.

Замечание. Все свойства остаются справедливыми, если вместо строк взять

столбцы.