Определение эйлерового пути в графе

Одна из важных задач теории графов заключается в нахождении пути (маршрута), содержащего по одному разу все ребра графа. Этот путь называется эйлеровым путем (ЭП)или эйлеровой линией в графе, а задачу его нахождения называют задачей Эйлера. Графы, на которых существуют замкнутые эйлеровы линии, называют эйлеровыми графами.

На практике задача нахождения ЭП на графе может встретиться, например, при определении порядка регламентных проверок исправности каналов связи между звеньями какой-нибудь достаточно сложной системы, обслуживаемой одной ремонтной единицей.

Ответ на вопрос о существовании ЭП на графах дают теоремы Эйлера.

Теорема Эйлера для неориентированных графов: для того чтобы на графе существовал замкнутый эйлеров путь (маршрут), необходимо и достаточно, чтобы граф был связным и степени всех его вершин были четными [1, 8].

Теорема Эйлера для ориентированных графов: для того чтобы на ориентированном графе существовал замкнутый ЭП, необходимо и достаточно, чтобы граф был связным и для каждой его вершины полустепень исхода равнялась полустепени захода [1, 8].

Для нахождения ЭП на графе (если он существует - см. теорему Эйлера) удобно воспользоваться следующим алгоритмом (для неориентированного графа):

0. Задается начальный шаг итерации k =0. Задается начальная (она же и конечная в случае замкнутого ЭП) вершина ЭП V_{0 .} Если, например, V₀ = A₃, то это означает, что начальной вершиной ЭП на шаге k = 0 выбрана третья вершина графа. Все ребра графа считаются непомеченными. Число непомеченных ребер S равно числу ребер графа.

1. k=k+1. Определяются все вершины, непосредственно связанные непомеченными ребрами с вершиной V_k-1.

2. Определяется число S_k непомеченных ребер, инцидентных вершине V_k-1.

Если S_k= 1, то вторая вершина, инцидентная этому ребру, становится очередной вершиной V_k ЭП. Это ребро помечается. Возвращаемся на п. 1.

Если S_k >1, то среди вершин, смежных V_k-1, выбирается вершина с наименьшим номером k, которая становится очередной вершиной V_k ЭП. Ребро, соединяющее эту вершину с вершиной V_k-1,помечается. Возвращаемся на п. 1.

3. S_k = 0. Для вершины, принадлежащей полученному таким образом пути и имеющей непомеченные инцидентные ребра, строится цикл по непомеченным ребрам. Определение новой вершины этого цикла начинается с п. 1.

4. Построенный таким образом новый цикл объединяется с ранее построенным в вершине, с которой начиналось построение нового цикла.

5. Если в цикле есть еще вершины, имеющие непомеченные инцидентные ребра, то возвращаемся на п. 3. Если таких ребер нет, то ЭП найден.

Отметим, что выбор вершины с наименьшим номером нужен для того, чтобы была определенность при выборе вершины на каждом шаге. Можно, однако, предложить выбор вершин и с наибольшим номером.

В качестве примера рассмотрим задачу нахождения ЭП для графа (рис. 4.3). ЭП существует, так как степени всех вершин четные.

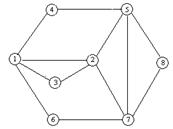Рис. 4.3

0. k = 0. Выберем начальную вершину с номером 3, т.е. V₀ = 3. Число непомеченных ребер S= 12.

1. k = 1. С вершиной V₀= 3 связаны вершины 1, 2.

2. Число непомеченных ребер для 3-й вершины S₁ = 2. Следующей вершиной ЭП является вершина с номером 1. Ребро 3-1 помечается. Возвращаемся к п. 1.

1. k = 2. С вершиной 1 связаны вершины 2, 4, 6.

2. S₂ = 3. Вершина 2. Помечается ребро 1-2. Возвращаемся к п. 1.

1. k = 3. С вершиной 2 связаны вершины 3, 5, 7.

2. S₃ = 3. Вершина 3. Помечается ребро 2-3. Возвращаемся к п. 1.

1. k = 4. С вершиной 3 связаны вершины 1, 2.

2. S₄ = 0. Вершин таких нет. Следовательно, получен цикл 3-1-2-3, который еще не является ЭП.

3. Вершины 1 и 2, входящие в этот цикл, имеют непомеченные инцидентные ребра. Рассмотрим вершину 1 в качестве начальной точки следующего цикла A₄ = 1.

1. k = 5. Вершины 4, 6.

2. S₅ = 2. Вершина 4. Ребро 1-4.

1. k = 6. Вершина 5.

2. S₆ = 1. Вершина 5. Ребро 4-5.

1. k = 7. Вершины 2, 7, 8.

2. S₇ = 3. Вершина 2. Ребро 5-2.

1. k = 8. Вершина 7.

2. S₈ = 1. Вершина 7. Ребро 2-7.

1. k = 9. Вершины 5, 6, 8.

2. S₉= 3. Вершина 5. Ребро 7-5.

1. k = 10. Вершина 8.

2. S₁₀ = 1. Вершина 8. Ребро 5-8.

1. k = 11. Вершина 7.

2. S₁₁ = 1. Вершина 7. Ребро 8-7.

1. k = 12. Вершина 6.

2. S₁₂ = 1. Вершина 6. Ребро 7-6.

1. k = 13. Вершина 1.

2. S₁₃ = 1. Вершина 1. Ребро 6-1.

1. k = 14. Вершин, связанных непомеченными ребрами, нет.

3. S₁₄ = 0. В найденных циклах нет вершин, имеющих инцидентные непомеченные ребра.

4. Для нахождения ЭП необходимо объединить два найденных цикла 3-1-2-3 и 1-4-5-2-7-5-8-7-6-1 в вершине 1. Результатом объединения будет путь: 3-1-4-5-2-7-5-8-7-6-1-2-3.

5. Так как в этом пути нет вершин с непомеченными ребрами, то найденный путь является эйлеровым.