Работа 2. методы минимизации фал и их реализация на эвм

Цель работы: изучение алгоритмов минимизации функций алгебры логики (ФАЛ) в классе ДНФ и анализ их применения на базе ЭВМ.

Задание

1. Минимизировать заданную ФАЛ 3-х переменных методом неопределенных коэффициентов. Записать СкДНФ, все ТДНФ, МДНФ. Проанализировать возможность применения метода для минимизации ФАЛ большего числа переменных.

2. Минимизировать вручную заданную ФАЛ 5-ти переменных методом Квайна – Мак-Класки. Записать СкДНФ, найти все ТДНФ используя ЛФП, выбрать все МДНФ.

3. Минимизировать ФАЛ из пп.1и2 и заданную ФАЛ 4-х переменных методом карт Вейча. Записать МДНФ.

4. Минимизировать ФАЛ из лабораторной работы №1 методом карт Вейча. Записать МДНФ. (п. 4 выполняется индивидуально каждым членом бригады)

5. Минимизировать ФАЛ из п.п. 1 и 2 на ЭВМ с помощью программы, разработанной на кафедре 302. Сравнить результаты ручного и машинного счета, сделать выводы.

6. Составить отчет. Ответить на контрольные вопросы.

Методические указания

Методы минимизации ФАЛ. Под минимальной формой записи ФАЛ 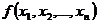в виде дизъюнктивной нормальной формы (МДНФ) понимается та ДНФ, которая содержит наименьшее число букв по сравнению с другими ДНФ данной функции. МДНФ существует для любой ФАЛ кроме константы 0 и может быть не единственной.

Решение задачи нахождения МДНФ 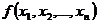может иметь следующие этапы:

1) Нахождение всех простых импликантов минимизируемой функции, дизъюнкция которых образует так называемую сокращенную дизъюнктивную нормальную форму (СкДНФ).

2) Формирование множества всех тупиковых ДНФ (ТДНФ) минимизируемой функции, соответствующих всем вариантам неупрощаемого покрытия множества Т₁ функции простыми импликантами.

3) Выделение из множества ТДНФ одной или нескольких МДНФ.

Наиболее трудоемкими, требующими применения специальных алгоритмов, являются 1-й и 2-й этапы. Существуют компьютерные реализации второго этапа поиска МДНФ: а) анализ импликантных матриц; б) составление и преобразование логической формулы покрытия (ЛФП). 3-й этап преодолевается путем перебора всех ТДНФ.

Для решения задачи нахождения МДНФ используются:

- метод расчленений и проб,

- метод карт Вейча,

- метод неопределенных коэффициентов,

- метод Квайна – Мак-Класски,

Последние два метода поддаются алгоритмизации и успешно реализуются на ЭВМ.

Метод расчленения и проб. ДНФ минимизируемой функции преобразуют с помощью основных аналитических соотношений [2], используя главным образом операции склеивания, поглощения и обобщенного склеивания. Однако далеко не каждая последовательность операций преобразования ФАЛ приводит к минимальной форме. Эффективность данного способа в значительной мере определяется квалификацией и опытом разработчика. Метод не формализован и применяется для функций, зависящих от небольшого числа аргументов.

Метод Карт Вейча. Описание карт Вейча и работа с ними описана в методических указаниях к лабораторной работе №1

При минимизации функцию наносят на соответствующую карту, ставя единицы в квадраты, соответствующие всем дизъюнктивным членам ФАЛ. Каждому минтерму максимального ранга соответствует один квадрат карты, а каждому минтерму меньшего ранга — несколько квадратов (2, 4, 8 и т.д.). Осуществляя минимизацию, выбирают совокупность минтермов по возможности меньшего ранга, которые покрывают все квадраты, содержащие единицы, и не покрывают остальные квадраты. При этом допускается, чтобы одна и та же единица была покрыта двумя и более минтермами. . Эти минтермы соответствуют простым импликантам функции, а их совокупность – МДНФ, одной из тупиковых ДНФ.

Наглядность, обеспечиваемая при этом, дает возможность “видеть” наиболее рациональные варианты покрытия множества Т₁ простыми импликантами и успешно находить МДНФ для функций не сложнее 5-6-местных. Для алгоритмизации метод карт Вейча не приспособлен.

При реализации метода расчленений и проб и метода карт Вейча нет необходимости выделять этапы 1, 2, 3, описанные выше.

Метод неопределенных коэффициентов.Основан на представлении минимизируемой n - местной ФАЛ в виде дизъюнкции всех возможных минтермов различного ранга от n переменных, причем каждый минтерм F_j в этой дизъюнкции логически умножается на неизвестный булевый коэффициент K_j - одноразрядное двоичное число.

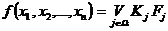(2.1)

Множество номеров W содержит все n-разрядные слова и все их собственные части, полученные заменой любой позиции (0,1) n-разрядного двоичного номера символом “-” (прочерк), что говорит об отсутствии соответствующей переменной в минтерме F_j. Очевидно, что общее число таких минтермов ранга не выше n и соответствующих им неопределенных коэффициентов равно 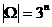. То есть в записи (2.1) предусмотрены все минтермы ранга не выше n.

Для n=2 получим:

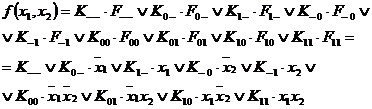
При такой форме записи ФАЛ задача минимизации сводится к выбору набора коэффициентов K_j , при котором полученная ДНФ соответствует заданной минимизируемой функции и содержит наименьшее число букв. Первое требование эквивалентно удовлетворению 2ⁿ ограничений, определяемых значениями ФАЛ на всех n-разрядных входных наборах.

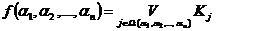. (2.2)

Для n=2 эти ограничения записываются в виде 4-х уравнений:

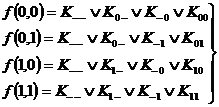
Заметим, что коэффициент 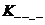отличен от нуля только тогда, когда минимизируемая функция совпадает с константой 1, поэтому можно принять 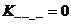и в дальнейшем этот коэффициент не записывать.

Система булевых уравнений (2.2) упрощается следующим образом. Все коэффициенты в уравнениях, левые части которых равны нулю, обнуляются и вычеркиваются из остальных уравнений. Для удовлетворения оставшихся уравнений достаточно принять равными 1 только коэффициенты при минтермах наименьшего ранга, а остальные коэффициенты в правых частях принимаются равными нулю. Минтермы, соответствующие не нулевым коэффициентам образуют множество всех простых импликантов минимизируемой функции, а их дизъюнкция – СкДНФ. Таким образом выполняется 1-й этап минимизации.

Работа на следующих этапах сводится к выбору из СкДНФ неизбыточного комплекта коэффициентов 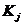, удовлетворяющего уравнениям (2.2) и соответствующего ДНФ с наименьшим числом букв. Для малых n это можно выполнить путем перебора. Для n³ 4 целесообразно воспользоваться специальными методами, рассмотренными ниже. Главным недостатком метода неопределенных коэффициентов является необходимость формирования и работы с множеством всех минтермов n переменных.

Более эффективным является анализ только тех минтермов, которые являются импликантами минимизируемой функции. На этой идее основан следующий метод минимизации.

Метод Квайна – Мак-Класски. Первый этап минимизации – нахождение СкДНФ, реализуется в соответствии с теоремой Квайна [3]: ”Для получения СкДНФ заданной ФАЛ необходимо и достаточно в ее СДНФ выполнить все возможные операции неполного склеивания, а затем все возможные операции поглощения ”. В методе Квайна он сводится к следующему:

1) Минимизируемую ФАЛ 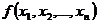представляют в виде СДНФ.

2) Все минтермы максимального n-го ранга пытаются попарно склеить по правилу неполного склеивания

,

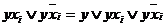где y – минтерм, не содержащий х_i . Все минтермы, участвующие в склеивании, отмечаются. Вновь полученные минтермы (n – 1)-го ранга также попарно сравниваются, склеиваются между собой и отмечаются. Далее склеиваются минтермы (n – 2)-го ранга и т.д. Этот процесс продолжается до тех пор, пока склеивания возможны. Дизъюнкция полученных минтермов содержит все минтермы – импликанты функции .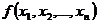

3) Вычеркиванием всех отмеченных минтермов реализуются все возможные поглощения, в результате остаются только простые импликанты, образующие СкДНФ (множество R).

В этом подходе есть одно существенное неудобство. Оно связано с необходимостью полного попарного сравнения всех минтермов на этапе нахождения простых импликант. Поэтому в 1956 г. Мак-Класски предложил модернизацию первого этапа метода Квайна, существенно уменьшающую число сравнений минтермов. Суть предложенной модернизации состоит в следующем. Записывают минтермы в виде их двоичных номеров и все номера разбивают по числу единиц в этих номерах на непересекающиеся группы. При этом в i-ю группу войдут все номера, имеющие в своей двоичной записи ровно i единиц. Попарное сравнение можно производить только между соседними по номеру группами, т.к. только эти группы отличаются для входящих в них минтермов в одном разряде. Склеивание возможно, если два номера различаются только по одной позиции. В результате склеивания образуется новый минтерм (номер), в котором на месте переменной, по которой производилось склеивание, ставится прочерк.

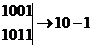- склеивание по переменной х₃ .

В результате склеивания минтермов n-го ранга получаются номера с одним прочерком, отвечающие минтермам (n-1)-го ранга. Минтермы, участвующие в склеивании, отмечаются. Полученные номера (n-1)-го ранга вновь группируются по числу единиц в номере, сравниваются, склеиваются и отмечаются до тех пор, пока склеивания возможны. Полученные в результате простые импликанты образуют СкДНФ. Модернизированный метод Квайна называют методом Квайна – Мак-Класски [4].

Анализ импликантной матрицы. Реализует 2-й этап минимизации. Импликантная матрица – таблица, столбцы которой соответствуют наборам из множества Т₁ минимизируемой ФАЛ, а строки – всем простым импликантам, найденным выше, и содержащая метки “\/” , отражающие факт покрытия каждым простым импликантом вершин из Т₁. Метка “\/” ставится на пересечении строки и столбца тогда, когда простой импликант является собственной частью минтерма n-ого ранга, соответствующего конкретной вершине из Т₁. Если простой импликант имеет ранг “k”, то в соответствующей строке импликантной матрицы будет 2^(n–k) меток.

Обработка импликантной матрицы может осуществляться по следующим правилам:

1. Если в каком-либо столбце импликантной матрицы есть только одна метка, то соответствующий простой импликант объявляется существенным и обязательно входит во все ТДНФ и МДНФ. При обнаружении существенного простого импликанта соответствующая строка импликантной матрицы и все столбцы, в которых она имеет метки, исключаются из дальнейшего рассмотрения (вычеркиваются).

2. После выявления всех существенных простых импликантов и упрощения импликантной матрицы исключаются пустые строки и дублирующие столбцы до тех пор, пока упрощения возможны.

3. Путем перебора выбирают все минимальные группы из оставшихся простых импликантов, совместно покрывающих незачеркнутые столбцы импликантной матрицы. При добавлении к ним существенных простых импликантов получаются все ТДНФ.

При больших размерностях упрощенной импликантной матрицы вышеуказанный перебор приближенно заменяют последовательным выбором и включением в состав наилучшего покрытия простых импликантов, имеющих наибольшее число меток; однако, получаемое при этом решение не гарантирует нахождение МДНФ.

Составление и преобразование логической формулы покрытия. Отражает формальную процедуру поиска всех тупиковых ДНФ [3, 5]. Логическая формула покрытия (ЛФП) выражает в форме r – местной ФАЛ 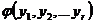условия покрытия вершин из множества Т₁ простыми импликантами из множества R. Пусть y_i – булевская логическая переменная, соответствующая i – му простому импликанту и отражающая факт покрытия j – той вершины из Т₁. Тогда импликантной матрице соответствует истиность ЛФП

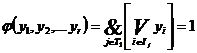, (2.3)

где: I_j - множество простых импликант, покрывающих j-ю вершину из Т₁.

Исходная форма левой части (2.3) есть КНФ, не содержащая инверсий переменных. В результате эквивалентных преобразований – раскрытия всех скобок и после выполнения всех возможных операций поглощения, получим МДНФ ЛФП.

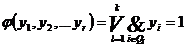(2.4)

Левую часть (2.4) можно трактовать как дизъюнкцию всех минимальных покрытий множества 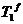, причем Q_l (l = 1,2,...k) – множество номеров простых импликантов, образующих конкретную ТДНФ, k – количество всех тупиковых ДНФ. На этом задача нахождения множества всех ТДНФ решена.

Программная реализация методов минимизации ФАЛ. Для поиска МДНФ используется программа, написанная на языке C++. Вид экрана при работе по минимизации функций алгебры логики приведен на рис. 2.1.