Построение точечного прогноза и доверительного интервала для линейной многофакторной модели регрессии.

Построение точечного прогноза и доверительного интервала для линейной многофакторной модели регрессии.

Классическая нормальная линейная модель множественной регрессии

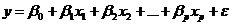
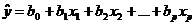
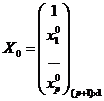
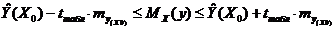
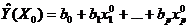
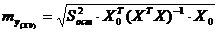
Корреляция для нелинейной регрессии. Средняя ошибка аппроксимации.

Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:

,

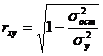где 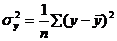– общая дисперсия результативного признака ,

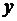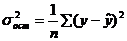– остаточная дисперсия.

Величина данного показателя находится в пределах: 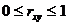. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.

Нелинейно относительно включенных в анализ объясняющих переменных, но линейная по оцениваемым параметрам.

При линеаризации принимает форму той же линейной парной регрессии, в этом случае для оценки тесноты связи может быть использован линейный коэффициент корреляции

Нелинейно по оцениваемым параметрам.

В этом случае линейный коэффициент корреляции по преобразованным переменным дает лишь приблизительную оценку связи и численное соотношение 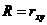не выполняется.

Средняя ошибка аппроксимации.

Средняя ошибка аппроксимации оценивает точность модели.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

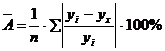
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем качестве подбора уравнения регрессии к исходным данным. Допустимый предел не более 8%-10%

Линейная модель множественной регрессии, основные предположения. Метод наименьших квадратов как основной метод оценивания параметров регрессии.

Линейная модель множественной регрессии формулируется следующим образом:

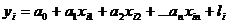
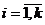
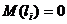
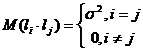
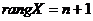
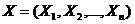
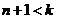
- не зависит от номера наблюдения

Для множественной регрессии более удобна матричная форма:

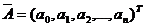- вектор столбца параметров

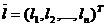
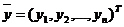
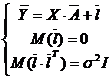
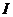– единичная матрица размерностью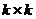

Метод наименьших квадратов:

Требуется подобрать такие оценки параметров регрессии 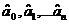, при которых регрессионные (сглаженные) значения 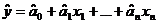как можно меньше от соответствующих статистических (наблюдаемых)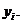

В качестве меры расхождения выбирается разность:

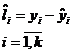
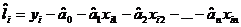
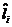- невязки

Значения 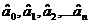надо выбрать такими, чтобы минимизировать интегрирующий характер невязок 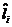(по всем имеющимся наблюдением).

В методе наименьших квадратов за такую характеристику принимается следующая величина:

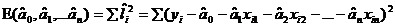
Таким образом, задача ставится так:

Выбрать величины 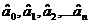так, чтобы невязка была минимальной:

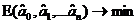
10. ?

11. ?

12. ?

13. ?

17. ?

18. ?

19. ?

Понятие об эконометрических моделях. Отличие эконометрических моделей от математических моделей. Спецификация и идентификация моделей.

Математически уравнение регрессионной связи записывается следующим образом:

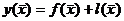
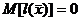
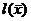- остаточная составляющая (регрессионные остатки).

26. ?

27. ?

28. ?

Построение точечного прогноза и доверительного интервала для линейной многофакторной модели регрессии.