Использованием булева выражения и таблицы истинности.

Сумматор двух одноразрядных слагаемых называют полусумматором и обозначают HS-HALT SUM- половина суммы.

Чтобы не было путанницы в обозначении логических и арифметических действий при описании арифметических устройств знаком + будем обозначать только арифметическую сумму,а знаком \/ - логическую функцию ИЛИ, логическое сложение. Знак +

будет означать сумму по модулю 2 для арифметических двоичных переменных и функцию исключающее ИЛИ для логических.

При сложении двух многоразрядных двоичных чисел кроме двух кроме двух входов слагаемых в сумматоре каждого разряда должен быть еще вход для переноса из младшего разряда.Полусумматор имеет только два входа а значит пригоден для сумирования только самого младшего разряда слагаемых, и не пригоден для суммирования всех других разрядов слагаемых.

Для сложения любого разряда двух слагаемых с учетом переноса из младшего разряда предназначен одноразрядный полный сумматор или просто сумматор.

Сумматор можно построить из дух полусумматоров. Первый полусумматор HS1 складывает два слагаемых и вырабатывает промежуточные сумму S_i ^/ и перенос P_i^/ . Второй полусумматор HS2 суммирует перенос с предидущего разряда P_i-1 c промежуточной суммой S_i^/,в результате получаетя полная сумма S_i.Перенос получется при участии двух HS и дополнительного ЛЭ ИЛИ.Схема SM по этим минимизированным выражениям на ЛЭ И-ИЛИ-НЕ испорльзуется в качестве основы в микросхемах 155ИМ1, 2, 3.

Здесь выходы P_i и S_i инверсные, что требует применения дополнительных инверторов.

А В р _ _

= АВ + АВ = А + В

0 0 0 0

0 1 0 1 P = А* В

1 0 0 1

1 1 1 0 Булевы выражения для полусумматора.

Таблица истинности полусумматора.

Структурная схема полусумматора

Билет20

1) ) Различия между позиционными и непозиционными системами счисления.

Все современные системы счисления (кроме некоторых римских цифр) являются позиционными, т.е. в них одна и та же цифра в разных позициях (слева, справа) имеет разное значение. Например в десятичном числе 55 левая цифра означает 50, а правая – только 5. В общем виде в позиционной системе счисления с основанием системы Х число А можно представить в виде:

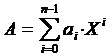
где n – количество разрядов числа А, а_i – коэффициенты каждого разряда, которые могут принимать значения от 0 до Х – 1.

При необходимости основание системы счисления указывается внизу после числа в виде нижнего индекса.

ПРИМЕРЫ:

1. Четырехразрядное десятичное число:

5685₁₀ = 5×10³ + 6×10² + 8×10¹ + 5×10⁰ ,

где Х = 10 – основание системы счисления, а₀ = 5, а₁ = 8, а₂ = 6,

а₃ = 5 – коэффициенты в каждом разряде, n = 4 – количество разрядов числа А.

2. Трехразрядное восьмеричное число:

372₈ = 3×8² + 7×8¹ + 2×8⁰ = 106₁₀

где Х = 8 (восьмеричная система счисления), коэффициенты в разрядах числа A а₀ = 2, а₁ = 7, а₂ = 3; n = 3 – количество разрядов числа А.

3. Двухразрядное шестнадцатеричное число:

4E₁₆ = 4×16¹ + 14×16⁰ = 78₁₀

где Х = 16 (шестнадцатеричная система счисления), коэффициенты в разрядах числа А а₀ = E = 14, а₁ = 4 (шестнадцатеричные цифры от 0 до 9 записываются так же, как и соответствующие десятичные цифры, а шестнадцатеричные цифры 10,11,12,13,14,15 записываются заглавными латинскими буквами А,В,С,D,Е,F соответственно); n = 2 – количество разрядов числа А.

4. Четырехразрядное двоичное число:

1101₂ = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 13₁₀

где X = 2 – двоичная система счисления, коэффициенты в разрядах числа А а₀ = 1, а₁ = 0, а₂ = 1, а₃ = 1, n = 4 – количество разрядов числа А.

Двоичную цифру, которая может принимать только два значения: 0 или 1, называют "бит", происходящее от сокращения BIT английских слов BI NARY DIGI T – "двоичная цифра".

Десятичная система, к которой мы привыкли, основана на количестве пальцев рук и для применения в цифровой технике неудобна. В цифровой аппаратуре устройства обычно имеют два рабочих состояния и в них применяют двоичную систему счисления. Восьмеричная и шестнадцатеричная системы счисления являются как бы компромиссными между двоичной и десятичной системами счисления и применяются в вычислительной технике из–за удобства представления больших двоичных чисел.

Б20

2) Три особенности КМОП мультиплексоров.

КМОП мультиплексоры строятся на основе дешифраторов и двунаправленных ключей коммутации. Поскольку ключи двунаправленные, то их выходы можноиспользовать как входы, значит мультиплексор можно использовать как демультиплексор. Наличие входа Е разрешения позволяет закрыть сразу все ключи – это равносильно тому, что выход мультиплексора и выходы демультиплексора имеют третье Z-состояние с высоким выходным сопротивлением.

КМОП мультиплексоры могут коммутировать не только цифровые, но и алалоговые сигналы.

Билет21

1) Порядок построения схем на основе булевых выражений.

Как правило, построение и расчет любой схемы осуществляется начиная с ее выхода.

Допустим задано булево выражение :

F =`B A + B`A + C`B.

Первый этап: выполняется логическое сложение, логическую операция ИЛИ, считая входными переменными функции `B A, B`A и C`B:

Второй этап: к входам элемента ИЛИ подключаются логические элементы И, входными переменными которых являются уже A, B, C и их инверсии:

Третий этап: для получения инверсий `A и`B на соответствующих входах ставят инверторы:

Данное построение основано на следующей особенности, – поскольку значениями логических функций могут быть только нули и единицы, то любые логические функции могут быть представлены как аргументы других более сложных функций.

Таким образом, построение комбинационной логической схемы осуществляется с выхода ко входу.

Б21

2)Дешифратор. Определение, назначение, условное графическое обозначение и описание с помощью булевого выражения и таблицы истинности.

Дешифратор преобразует входной двоичный код в такой выходной код , в котором только на одном из всех выходов дешифратора имеется активный уровень. Такой выходной код называется унитарным или унарным. В положительной логике активным является высокий уровень, но для большинства ТТЛ дешифраторов активным является низкий уровень. Номер активного выхода соответствует двоичному входному коду.

Полным называют дешифратор, m выходов которого используют все возможные наборы n входных переменных, т.е. m =2ⁿ .

Если число выходов меньше, то такой дешифратор называется неполным(m<2ⁿ).

. Дешифраторы используют когда нужно обращаться к различным цифровым устройствам, и при этом номер устройства – его адрес – представлен двоичным кодом, поэтому входы дешифратора иногда называют адресными входами, и обычно их нумеруют не порядковыми номерами 0, 1, 2, 3, 4, 5…, а в соответствии с двоичными весами разрядов 1, 2, 4, 8, 16 … В соответствии с числом входов и выходов дешифраторы называют 3-8 (три в восемь) , 4-16, 4-10 (неполный).

Вход Е (ENABLE-разрешение) называют разрешающим , стробирующим ,управляющим . Так как через вход Е можно передавать информацию (данные) на какой либо из выходов (или на все выходы поочередно),то дешифратор , имеющий Е вход иногда называют демультиплексором и обозначают соответственно DMX (DEMULTIPLEXER) или DX.

Булевы выражения

Y0 = а₁ a₂ a₄ E

Y1 = a₁ a₂ a₄ E

Y2 = a₁ a₂ a₄ E

Y3 = a₁ a₂ a₄ E

Y4 = a₁ a₂ a₄ E

Y5 = a₁ a₂ a₄ E

Y6 = a₁ a₂ a₄ E

Y7 = a₁ a₂ a₄ E

Таблица истинности

Е	а4	а2	а1	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
	X	X	X

Иногда входов Е бывает несколько , причем часть их может быть прямыми , а часть инверсными входами . Тогда их обычно отделяют на поле(правом) чертой от остальных входов.

Билет22

1) Прямой код со знаковым разрядом

6 = 0110

-6 = 10110

Обратный код

-6 = 1 1001

Дополнительный код

-6 = 1 1001 1001=10 10000=16 10-16=-6

2) НЕТУ НИХЕРА

Билет23

1)Отрицательная логика, ее применение. (1

Логика называется положительной, если высокий потенциал отображает единицу, а низкий, – ноль. Если наоборот, высокий потенциал отображает ноль, а низкий, – единицу, то логика называется отрицательной. Данное правило называют логическим соглашением.

Самым важным следствием применения отрицательной логики является то, что при переходе от положительной логики к отрицательной функция И превращается в ИЛИ, и наоборот.

Это можно проиллюстрировать следующим образом:

– в положительной логике, – в комнате зимой Тепло, если батареи отопления Включены И окна Закрыты ( Т = ВЗ);

– в отрицательной логике, – в комнате зимой НЕ Тепло, если батареи отопления НЕ Включены ИЛИ окна НЕ Закрыты ( `Т = `В+ `З).

Здесь И переходит в ИЛИ когда входные аргументы и вывод отрицаются, при этом смысл выражения практически не меняется.

Благодаря этому переходу от И к ИЛИ и удается с помощью однотипных элементов инвертирующего базиса получать все остальные логические функции. Об этом говорят два постулата де 'Моргана: АВ = `А + `В; А + В = `А`В.

Для доказательства одного из них составим таблицу истинности функции И:

А В F

––––––––––––

0 0 0

0 1 0

1 0 0

1 1 1

Перепишем эту таблицу в символах уровней потенциалов Н – High, высокий ; L – Low, низкий , считая ее записанной для положительной логики:

А В F

––––––––––––

L L L

L H L

H L L

H H H

Последняя таблица не зависит от вида логики и характеризует работу технического устройства (логического элемента), который при положительной логике является элементом И. Определим чем же является это устройство при отрицательной логике. Снова возвратимся к нолям и единицам, учитывая их эквивалент для отрицательной логики:

А В F

––––––––––––

1 1 1

1 0 1

0 1 1

0 0 0

Полученная таблица истинности соответствует элементу ИЛИ. Следовательно, рассмотренный логический элемент в отрицательной логике является логическим элементом ИЛИ. Отсюда общий вывод: если логический элемент в положительной логике реализует функцию И, то в отрицательной логике этот же элемент реализует функцию ИЛИ, и наоборот, логический элемент ИЛИ положительной логики реализует функцию И в отрицательной логике.

Применение наряду с положительной логикой и отрицательной логики позволяет любое сложное логическое преобразование выполнить с применением только логических элементов И – НЕ или только ИЛИ – НЕ.