Различие между непрерывным и двоичным (цифровым) сигналом. Последовательные и параллельные двоичные сигналы. (2)

Последовательные двоичные сигналы хорошо использовать при передаче данных на большие расстояния, когда прокладывать многожильный кабель для параллельного двоичного сигнала становится достаточно дорого, ведь в отличие от последовательного параллельный сигнал передается одновременно по нескольким линиям, как это показано на рис.2.1.3. В приведенном примере параллельного сигнала совокупность нулей и единиц во время первого тактового импульса соответствует числу 3, а во втором, – 10.

Обычно передача цифровых данных на расстояние до нескольких метров производится с помощью параллельных сигналов, а на большие расстояния, – с помощью последовательных сигналов.

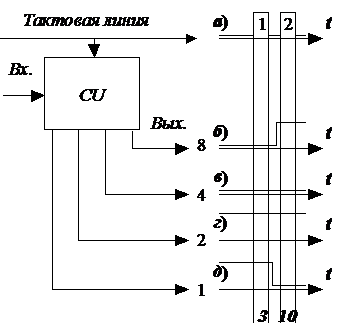
Рис.2.1.3. Пример параллельного двоичного сигнала, поступающего одновременно с нескольких выводов цифрового устройства CU, в котором:

а)– сигнал передаваемый по тактовой линии;

б) – сигнал, поступающий с старшего выхода цифрового устройства CU, которому соответствует весовой коэффициент 8;

в) – сигнал, поступающий с среднего выхода цифрового устройства CU, которому соответствует весовой коэффициент 4;

г) – сигнал, поступающий с среднего выхода цифрового устройства CU, которому соответствует весовой коэффициент 2;

д) – сигнал, поступающий с младшего выхода цифрового устройства CU, которому соответствует весовой коэффициент 1.

Как видно из трех вышеприведенных рисунков, самым быстрым способом передачи информации является использование параллельного сигнала, но при этом требуются самые большие аппаратные затраты.

Самым медленным, но зато и самым простым и требующим самые малые затраты оборудования, является применение число–импульсного сигнала.

Последовательный позиционный двоичный сигнал является промежуточным между параллельным и число–импульсным сигналами.

Б14

2)Приоритетный шифратор. Условное графическое обозначение.

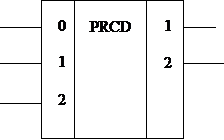
Шифратор (кодер) — (англ. encoder) логическое устройство, выполняющее логическую функцию (операцию) — преобразование позиционного n-разрядного кода в m-разрядный двоичный, троичный или k-ичный код.

НА входе приоритетного шифратора стоит схема выделения старшей единицы, в которой все входные единицы,кроме старшей, заменяются нулями.

Билет15

1)Отрицательная логика, ее применение. (1

Логика называется положительной, если высокий потенциал отображает единицу, а низкий, – ноль. Если наоборот, высокий потенциал отображает ноль, а низкий, – единицу, то логика называется отрицательной. Данное правило называют логическим соглашением.

Самым важным следствием применения отрицательной логики является то, что при переходе от положительной логики к отрицательной функция И превращается в ИЛИ, и наоборот.

Это можно проиллюстрировать следующим образом:

– в положительной логике, – в комнате зимой Тепло, если батареи отопления Включены И окна Закрыты ( Т = ВЗ);

– в отрицательной логике, – в комнате зимой НЕ Тепло, если батареи отопления НЕ Включены ИЛИ окна НЕ Закрыты ( `Т = `В+ `З).

Здесь И переходит в ИЛИ когда входные аргументы и вывод отрицаются, при этом смысл выражения практически не меняется.

Благодаря этому переходу от И к ИЛИ и удается с помощью однотипных элементов инвертирующего базиса получать все остальные логические функции. Об этом говорят два постулата де 'Моргана: АВ = `А + `В; А + В = `А`В.

Для доказательства одного из них составим таблицу истинности функции И:

А В F

––––––––––––

0 0 0

0 1 0

1 0 0

1 1 1

Перепишем эту таблицу в символах уровней потенциалов Н – High, высокий ; L – Low, низкий , считая ее записанной для положительной логики:

А В F

––––––––––––

L L L

L H L

H L L

H H H

Последняя таблица не зависит от вида логики и характеризует работу технического устройства (логического элемента), который при положительной логике является элементом И. Определим чем же является это устройство при отрицательной логике. Снова возвратимся к нолям и единицам, учитывая их эквивалент для отрицательной логики:

А В F

––––––––––––

1 1 1

1 0 1

0 1 1

0 0 0

Полученная таблица истинности соответствует элементу ИЛИ. Следовательно, рассмотренный логический элемент в отрицательной логике является логическим элементом ИЛИ. Отсюда общий вывод: если логический элемент в положительной логике реализует функцию И, то в отрицательной логике этот же элемент реализует функцию ИЛИ, и наоборот, логический элемент ИЛИ положительной логики реализует функцию И в отрицательной логике.

Применение наряду с положительной логикой и отрицательной логики позволяет любое сложное логическое преобразование выполнить с применением только логических элементов И – НЕ или только ИЛИ – НЕ.