Умножение и деление многоразрядных двоичных чисел.
Суммирование многоразрядных двоичных чисел одноразрядным сумматором
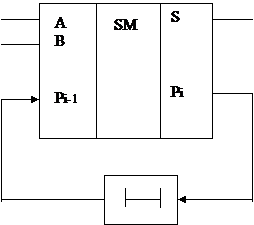
Для того, чтобы правильно суммировать многоразрядные двоичные числа, надо на входы А и В подавать эти числа последовательно, начиная с младшего разряда. Время задержки между подачами разрядов должно соответствовать времени задержки в блоке обратной связи(оно должно быть больше, чем длительность переходных процессов в сумматоре).
В простейшем случае элемент задержки может быть выполнен в виде RC цепочки, но чаще всего используют триггерные схемы, которые тактируются (синхронизируются) теми же тактами, что и регистры, подающие разряды А и В входного кода.
 | |||
 |
Элемент задержки
Билет8
1)8421(BCD) код и код Грея.
Здесь знак Å означает сумму по модулю два, которая равна единице, если входные слагаемые разные, или, – нулю, если они одинаковые, т.е.:
0 Å 0 = 0
0 Å 1 = 1
1 Å 0 = 1
1 Å 1 = 0
Число в коде Грея можно также получить из двоичного кода следующим образом :



 двоичный код 1 1 0 1 0 1
двоичный код 1 1 0 1 0 1
 | |||
 | |||
 |

Å Å Å Å Å
 | |||
 |
 код Грея 1 0 1 1 1 1
код Грея 1 0 1 1 1 1
Обратное преобразование кода Грея в двоичный код производят по похожей схеме:



 код Грея 1 0 1 1 1 1
код Грея 1 0 1 1 1 1
 | |||
 | |||
 |

Å Å Å Å Å
 | |||||
 | |||||
 |
 двоичный код 1 1 0 1 0 1
двоичный код 1 1 0 1 0 1
Свойство кода Грея изменяться только в одном разряде при последовательном переходе от одного числа к другому ближнему определяет его преимущество перед другими кодами при использовании этого кода для построения кодирующих дисков и пластин. Очевидно, что такое свойство кода уменьшает число переключений считывающих устройств и снижает неоднозначность считывания кода. Код Грея нельзя отнести к позиционным кодам, поскольку в нем весовые значения единиц в различных позициях нельзя однозначно определить по формуле, приведенной в начале данного раздела.
Б8
2)Полусумматор. Определение, условное графическое обозначение, схема и описание ее с
Отрицательная логика. Ее применение. (2)
Покажем это хотя бы для простейших функций булева базиса.
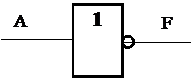 | |||
 |

 НЕ:
НЕ:
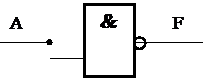 | |||||
 | |||||
 |


|
|
|
|
 | |||||
 | |||||
 | |||||
|
|

|





|

|




 ИЛИ :
ИЛИ : 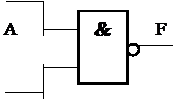 | |||
 | |||
| |

|
|
 Приведeнные на этих рисунках построения логических функций НЕ, И, ИЛИ выполнены с помощью только логических элементов 2И – НЕ.
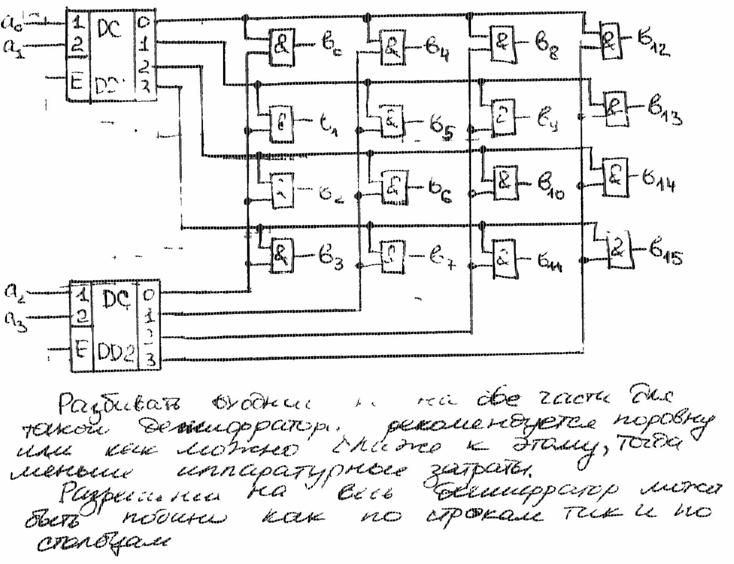
Приведeнные на этих рисунках построения логических функций НЕ, И, ИЛИ выполнены с помощью только логических элементов 2И – НЕ.Матричный дешифратор.
Умножение и деление многоразрядных двоичных чисел.
2) Умножение столбиком
0 1 1 0 =5
0 1 0 1 =6
0 1 1 0
0 0 0 0
0 1 1 0
0 1 1 1 1 0 30
Деление
Помещаем делитель под делимым как можно левее, производим вычитание из делимого, после вычитания в наиболее значимый разряд частного заносится 1, если вычитание невозможно из-за того что остаток оказывается отриц вычитание не выполняется и в наиб значимый разряд частного заносится 0. затем сдвигаем весь делитель на одну позицию вправо и втом же духе.
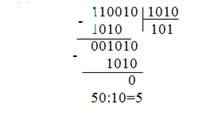

Делимое больше делителя Делимое меньше делителя
Билет2
- Три способа задания отрицательных чисел с примерами.
1) Прямой код со знаковым разрядом
6 = 0110
-6 = 10110
Обратный код
-6 = 1 1001
Дополнительный код
-6 = 1 1001 1001=10 10000=16 10-16=-6
2)Матричный дешифратор.
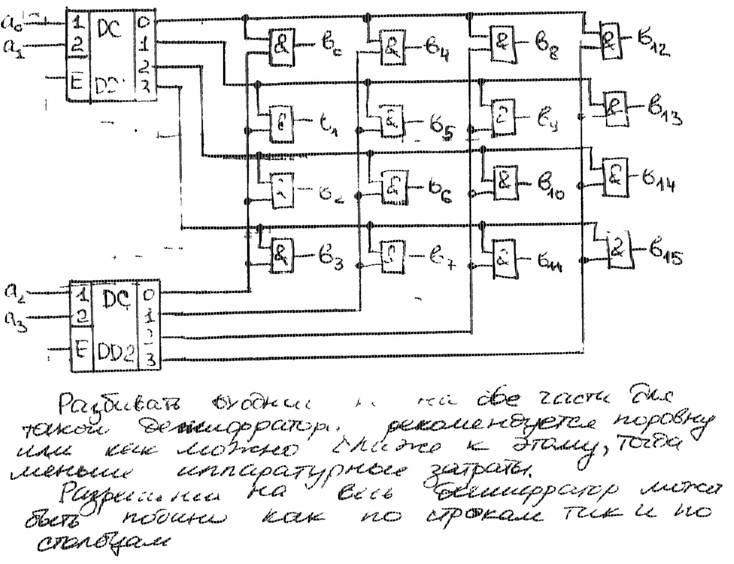
Билет 3
1)Минимизация булевых выражений по картам Карно. (1
Основой минимизации алгебраическим способом является последовательное использование законов булевой алгебры и правил преобразований. Карта Карно изображает в виде графических квадратов (клеток) все возможные комбинации переменных, причем переменные, определяющие координаты клеток карты, размещают так, чтобы при переходе из одной клетки в соседнюю, как по горизонтали, так и по вертикали, изменялась только одна переменная.
Если требуется получить карту Карно для какой–либо функции, сначала надо записать эту функцию в СДНФ, – в совершенной дизъюнктивно нормальной форме, или в виде таблицы истинности.
Каждое слагаемое булева выражения в СДНФ, или каждая единица в столбце функции таблицы истинности, задается на карте Карно единицей в соответствующей клетке. Координаты этой клетки содержат те же входные переменные и их инверсии, что и данное слагаемое СДНФ булева выражения ( или данная строка таблицы истинности ).
Таблица истинности для четырех переменных включает 16 строк, следовательно карта Карно должна состоять из 16 клеток, как показано на рис.4.10.1.
`А`В `А В А В А`В
 |
`С`D 1 1
 |
`C D 1 1
 |
C D 1 1
 |
C`D

Рис.4.10.1. Пример карты Карно для 4–х переменных.
У карты Карно для четырех переменных клетки крайнего левого столбца должны рассматриваться как соседние для клеток крайнего правого столбца, а клетки верхней строки, – как соседние для клеток нижней строки. Другими словами можно сказать, что эта карта расположена на поверхности цилиндра (склеили правый край карты с левым ), изогнутого и растянутого так, что его верхний срез соединяется с нижним срезом; при этом цилиндр превращается в тор (бублик).
Правила упрощения заполненной карты Карно для четырех переменных заключаются в следующем :
– соседние две, четыре, или восемь единиц обводят общим контуром;
– контур должен быть прямоугольным без изгибов или наклонов;
– каждый контур превращает все входящие в него единицы в одну, т.е. объединенные таким образом слагаемые СДНФ булева выражения дают одно слагаемое в упрощенном выражении;
– те входные переменные, которые входят в координаты данного контура совместно со своими инверсиями, исключаются из слагаемого, которое дает этот контур в упрощенное выражение.
Примеры упрощения булевых выражений с помощью карты Карно:
1. F1 = `А В`С`D1 + A B`C`D2 +`A B`C D3 + A B`C D4 +
+ `A`B C`D5 + `A B C`D6 .
