Основные правила дифференцирования. Сумма.

Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х0 обозначаются для краткости так: u(х0) = u, v(х0) = v, u'(х0) = u', v'(х0)=v`. Если функции u и v дифференцируемы в точке х0, то их сумма дифференцируема в этой точке и

(u+v)' = u' + v'

Коротко говорят: производная суммы равна сумме производных.

1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х0+Δx)+ v(х0+Δx) – (u(х0)+v(х0)) = (u(х0+Δx)-u(х0)) + (v(х0+Δx)-v(х0)) = Δu + Δv

2)

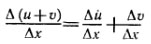
3) Функции u и v дифференцируемы в точке х0, т. е. при Δх→0

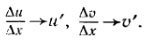
Тогда,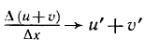

при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’

Лемма. Если функция f дифференцируема в точке х0, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е.

f(х0 + Δх)→f (х0) при Δx→0

Действительно,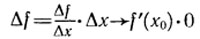

при Δх→0, так как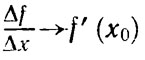

Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х0 + Δx)→f (х0) при Δх→0.

34. Производная функции. Геометрическое и формальное определение.

Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

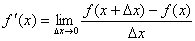
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.

33. Бесконечные пределы и односторонние пределы

Правосторонней проколотой полуокрестностью точки радиуса а радиуса б, называется Интервал(а, а+б) . Левосторонней проколотой полуокрестностью точки а радиуса б ,обозначается, называется интервал( а-б,а) .

Определение 1.1 (правостороннего предела).Пусть f(x) функция, определенная в

некоторой правосторонней проколотой полуокрестности некоторой точки a . Число L

называется правосторонним пределом функции f(x) при xстремящемся к числу a

справа и обозначается L= limf(x) , если значения f(x) можно сделать как угодно

близкими к L , беря иксы в правосторонней проколотой полуокрестности точки

достаточно малого радиуса.

Аналогично определяется левосторонний предел.

Бесконечныепределы.

32. Первый замечательный предел. Второй замечательный предел

Первым замечательным пределом называется предел

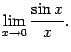
Вторым замечательным пределом называется предел

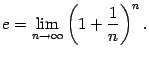
31. Раскрытие неопределённостей при вычислении пределов методом преобразования функции

С непосредственным вычислением пределов основных элементарных функций разобрались.

При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.

Перечислим все основные виды неопределенностей: ноль делить на ноль (0 на 0), бесконечность делить на бесконечность , ноль умножить на бесконечность , бесконечность минус бесконечность , единица в степени бесконечность , ноль в степени ноль , бесконечность в степени ноль .

СЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.

Раскрывать неопределенности позволяет:

упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

использование замечательных пределов;

применение правила Лопиталя;

использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).

Пример:

Вычислить предел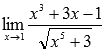

Решение: Подставляем значение:

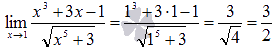
И сразу получили ответ!!!

Ответ: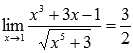

Билет № 41 Производная синуса и косинуса.

1) (sin х)' = cos х; 2) (cos х)' = — sin х.

Билет № 42. Экспонента, её производная и определение как показательной функциис основанием e.

Экспонента — показательная функция , где e — Число Эйлера ().

Производная показательной функции.

Теорема 1.

Функция ех дифференцируема в каждой точке области определения, и

(ех)' = ех.

Доказательство.

Найдем сначала приращение функции у = ех в точке x0:

Δy = e x0+Δx — е x0 = е x0 • е Δx — е x0 = е x0 (еΔ x — 1).

Пользуясь условием (1), находим:

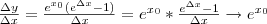
По определению производной отсюда следует, что у' = ex т. е. (еx)’= ех при любом х.

Число е положительно и отлично от 1, поэтому определены логарифмы по основанию е.

Определение.

Натуральным логарифмом (обозначается ln) называется логарифм по основанию е:

ln x = loge х.

(2)

По основному логарифмическому тождеству для любого положительного числа еln a =а. Поэтому ах может быть записано в виде

ax = (eln a)x = ex ln a. (3)

Выведем формулу производной показательной функции при произвольном значении а.

Теорема 2.

Показательная функция ах дифференцируема в каждой точке области определения, и

(аx)'=ахlп а.

(4)

Доказательство.

Из формулы (3) по теореме о производной сложной функции получаем, что показательная функция дифференцируема в каждой точке и

(ax)’= (ex ln a)’= ex lnaln a = ax ln a (5)

Следствие.

Показательная функция непрерывна в каждой точке своей области определения, т. е. аx →аx0 при х →х0.

Билет № 43 Уравнение касательной к графику функции.

Определение

Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.

А что будет, если производная в точке x0 не существует? Возможны два варианта:

Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).

Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x0) · (x − x0) + f (x0)

Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.

Задача

Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.

Решение

Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x0) и f ’(x0) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;

Теперь найдем производную: f ’(x) = (x3)’ = 3x2;

Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;

Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.

Это и есть уравнение касательной.

Ответ

y = 12x − 16

Задача

Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2.

Решение

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f (x0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;

f ’(x) = (2sin x + 5)’ = 2cos x;

f ’(x0) = f ’(π/2) = 2cos (π/2) = 0;

Уравнение касательной:

y = 0 · (x − π/2) + 7 ⇒ y = 7

Ответ

y = 7

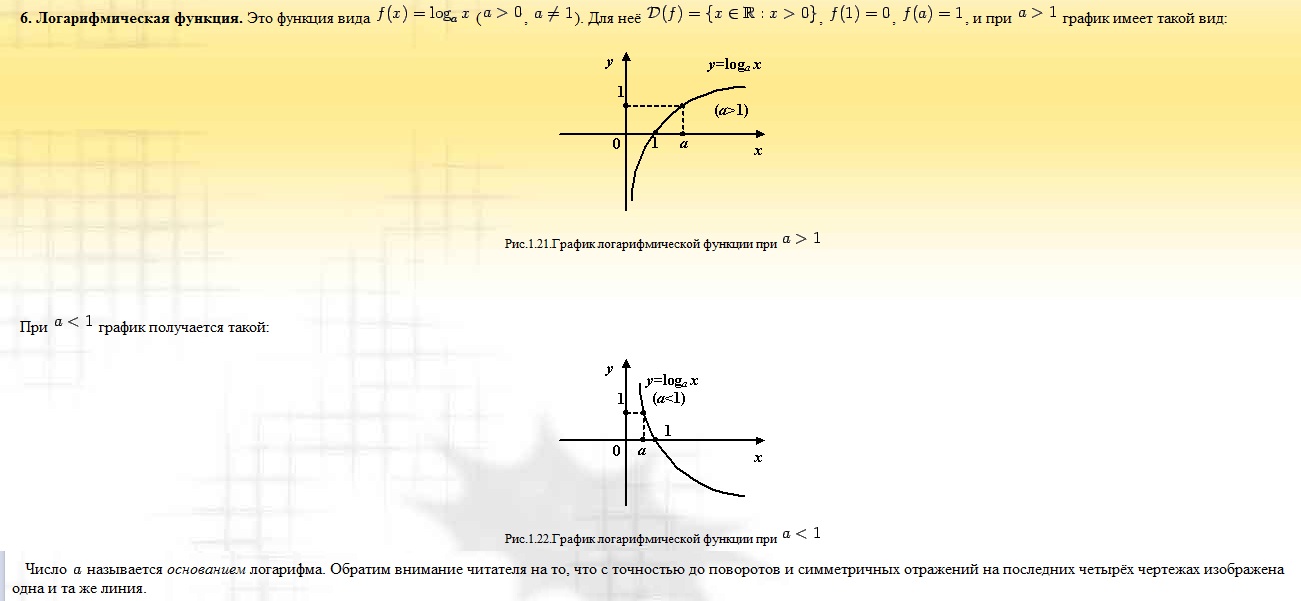
Билет № 44 Графики степенных функций, экспоненты и логарифма. Сравнение их

поведения (роста) на бесконечности.

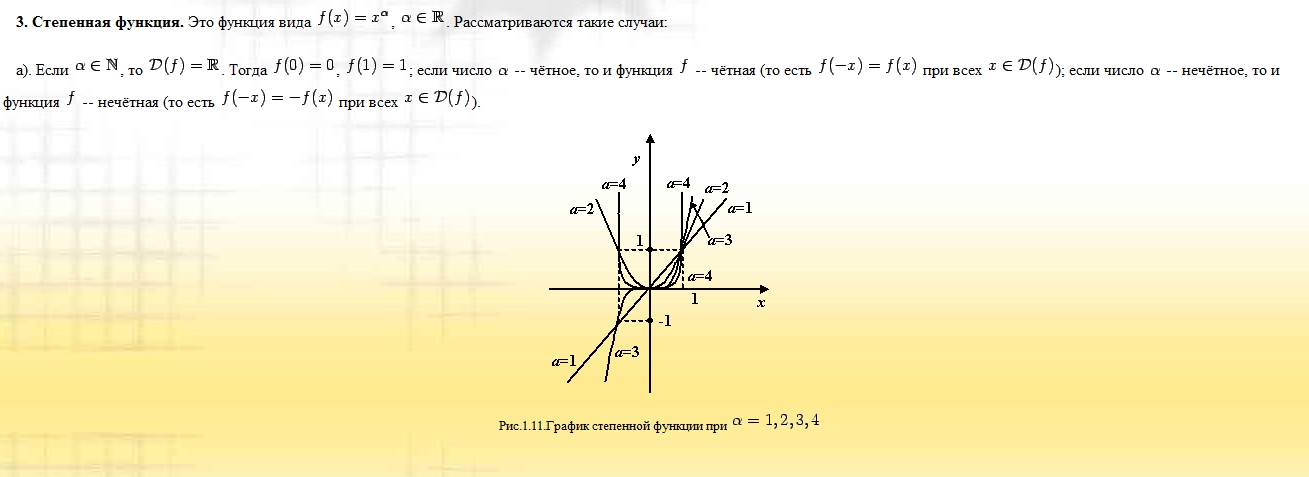
СТЕПЕННАЯ:

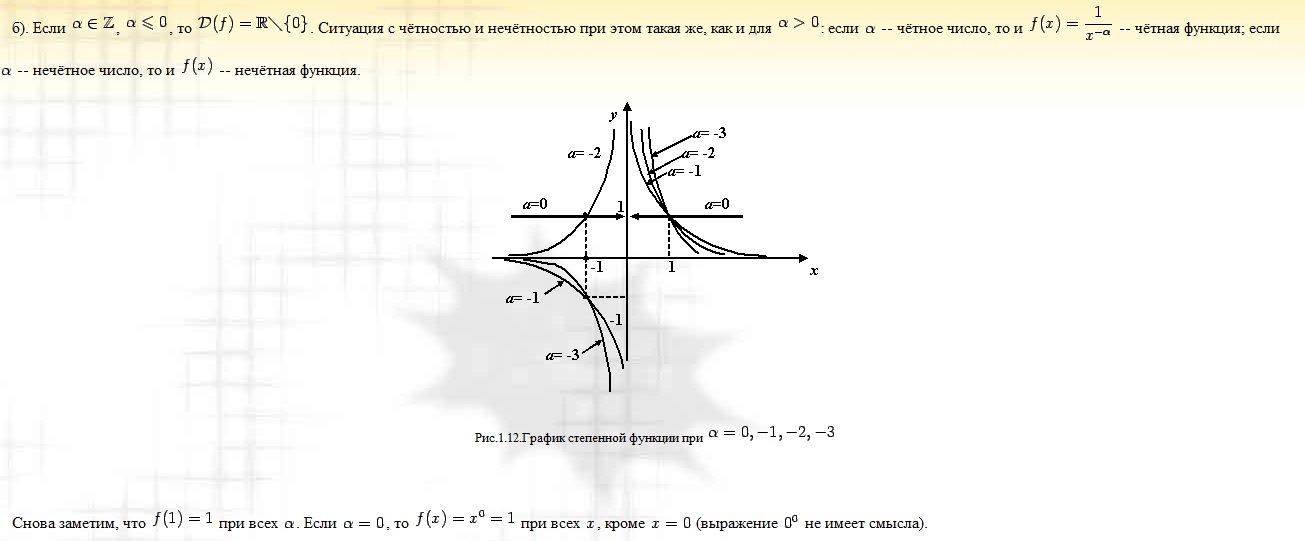
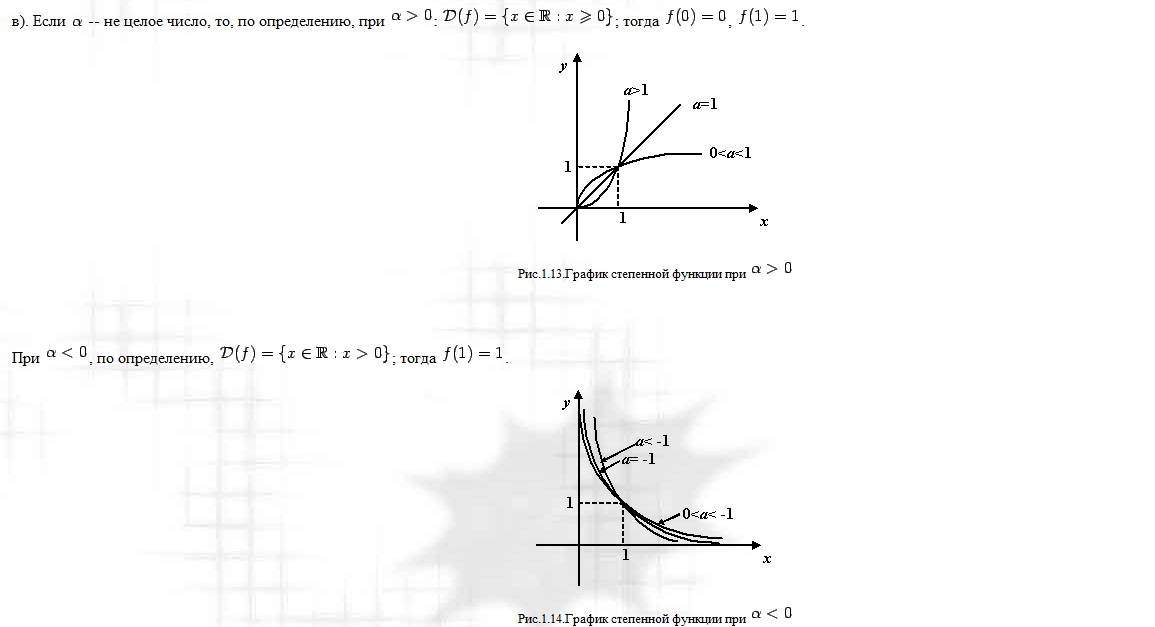
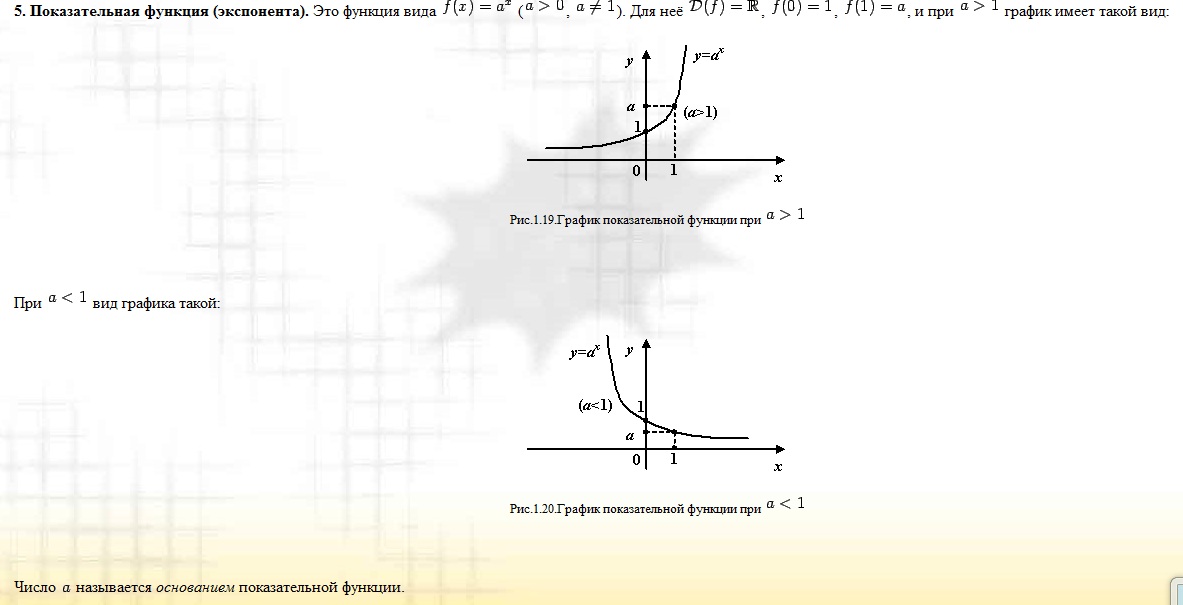
ЭКСПОНЕНТА:

ЛОГАРИФМА:

Билет № 45 Теорема о промежуточном значении, теорема Ролля и формула конечных приращений Лагранжа.

Теорема Ролля

Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю,f'(e) = 0.

Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Теорема Лагранжа

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e, a < e < b, такая, что

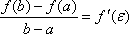
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

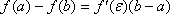
Определение. Выражение

азывается формулой Лагранжа или формулой конечных приращений.

Билет № 46 Правило Лопиталя

Билет № 47 Производные высших порядков.

Билет № 48 Исследование функций с помощью производных первого и второго порядка на максимум и минимум.