Формулы синуса разности двух углов

sin (α — β) = sin α • cos β — sin β • cos α

Формулы косинуса разности двух углов

cos (α — β) = cos α cos β + sin α sin β

Синус,косинус,тангенс двойного угла

· sin 2α = 2 sin α cos α = tg α / (1 + tg²α),

· cos 2α = cos²α – sin²α = 2 cos²α – 1 = 1 – 2 sin²α = (1 – tg²α) / (1 + tg²α),

· tg 2α = 2 tg α / (1 – tg²α)

Синус косинус тангенс половинного угла

Сумма и разность синусов

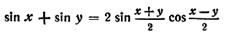
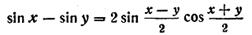
Сумма и разность косинусов

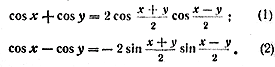
Арксинус угла

arcsin - тригонометрическая функция, арксинус.
arcsin(х) - это угол, синус которого равен "х", в том случае если "х" лежит в пределах от минус единицы до плюс единицы.

Арккосинус угла

Арккосинусом числа m называется такое значение угла x, для которого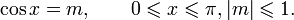

Функция 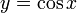непрерывна и ограничена на всей своей числовой прямой. Функция 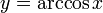является строго убывающей.

Арктангенс угла

Арктангенсом числа m называется такое значение угла 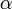, для которого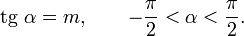

Функция 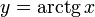непрерывна и ограничена на всей своей числовой прямой. Функция 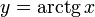является строго возрастающей.

Аргкотангенс угла

Арккотангенсом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Прямоугольная декартова

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.

Формула расстояние между двумя точками

Уравнение сферы

Уравнение сферы с центром A (a; b; c) и радиусом R имеет вид: (x – a)² + (y – b)² + (z – c)² = R².

Уравнение плоскости

Ax + By + Cz + D = 0

Уравнение прямой

y = k x+ b

Векторы , модуль вектора

Вектор — это элемент векторного пространства (некоторого множества с двумя операциями на нём, которые подчиняются восьми аксиомам).

Модулем (длиной) вектора 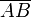называется длина(норма) соответствующего вектора 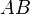и обозначается как .

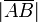Равенство вектора

Два вектора называются равными, если они совмещаются параллельным переносом.
Т.е. существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно.
Теорема
Если векторы одинаково направлены и равны по абсолютной величине, то они равны.

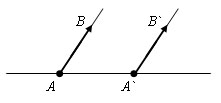
Сложение вектора

Суммой двух векторов 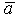и 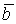называется вектор 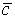, направленный из начала вектора 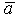в конец вектора 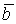при условии, что начало 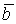совпадет с концом вектора .

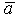Угол между векторами

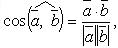
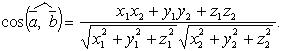
Разложение вектора по направлениям

Разложить вектор на составляющие векторы по двум заданным направлениям – это значит найти два вектора и :

– направления которых совпадают с заданными направлениями;

– векторная сумма которых равна вектору .

Геометрически разложить вектор на составляющие векторы – это значит построить параллелограмм по заданной диагонали и заданным направлениям.

Угол между векторами

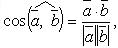
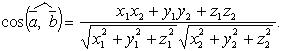
Проекция вектора на ось

Проекцией вектора 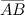на ось 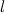называется длина отрезка 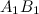, взятая со знаком "+", если направление 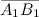совпадает с направлением вектора 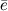, и со знаком "-", если направление 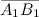противоположно направлению единичного вектора оси 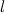(рис. 1).

Координаты вектора

На плоскости координаты вектора v относительно данного базиса (a, b) – это такая пара чисел (x; y), что v = xa + yb. Любой вектор имеет однозначно определенные координаты относительно любого базиса.