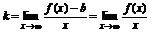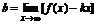Условия постоянства функции.
Теорема1. Пусть функция f(x) определена и непрерывна в промежутке и имеет внутри него конечную производную. Для того, чтобы f(x) была в Х постоянной, необходимо и достаточно, чтобы f’(x)=0 внутри Х.
Теорема2. Пусть функция определена и непрерывна на отрезке [a,b] и имеет конечную производную на (a,b). Для того, чтобы функция f(x) была монотонно возрастающей/убывающей на [a,b], необходимо и достаточно, чтобы выполнялось неравенство f’(x)³0 (f’(x)£ 0).
Точка минимума (максимума) функции f – точка х0, если существует окрестность этой точки такая, что для всех х из этой окрестности выполняется неравенство: f(x0)£f(x)
Точка экстремума – точка максимума или минимума.
Теорема1. Если точка х0 – точка экстремума функции f и существует f’(x0), то f’(x0)=0
Стационарные (критические точки, точки подозрительные на экстремум) – точки, в которых производная обращается в ноль.
Достаточные условия экстремума.
Для скалярной функции одной переменной достаточные условия экстремума формулируются с помощью первой производной или на основе высших производных.
Если при переходе через точку х производная функции f’(x):
1) меняет знак с «+» на «-», то в точке х – max.
2) меняет знак с «-»на «+»то в точке х – min.
3) не меняет знака, то экстремума нет.
Невырожденная квадратичная форма называется положительно определенной, если Q(x1,x2,…xn)>0 для любого вектора х=(х1,х2,…,хn) и называется отрицательно определенной, если для любого x =(х1,х2,…,хn) имеет место Q(x1,x2,…xn)<0.
Квадратичная форма называется неопределенной, если для одних х величина Q(x)>0, а для других Q(x)<0.
Теорема (критерий Сильвестра). Невырожденная квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры ее матрицы больше нуля, и является отрицательно определенной, если знаки главных миноров чередуются, начиная с отрицательного.
Выпуклость графика функции.
Выпуклым вверх (вниз) называется график функции, если все точки любой дуги графика лежат выше (ниже) хорды, соединяющей ее концы.
Теорема1. Если функция f(x) определена, непрерывна на [a,b] и имеет конечную производную на (a,b), то для того, чтобы график фун-и f(x) был выпуклым вверх (вниз), необходимо и достаточно, чтобы производная f’(x) убывала (возрастала).
Теорема2. Пусть f(x) определена на [a,b] и существует вторая производная f’’(x) на (a,b). Тогда для выпуклости вверх (вниз) графика функции необходимо и достаточно, чтобы было f’’(x)£0 (f’’(x)³0) на (a,b).
Точка перегиба графика функции, непрерывной в х0 – точка х0 перехода от выпуклости вниз к выпуклости вверх или наоборот.
Асимптоты графикафункции.
Асимптота – прямая L графика функции f(x), если при стремлении точки графика к бесконечности расстояние между точкой графика фун-и и прямой L стремится к нулю.
Вертикальные асимптоты (если хотя бы один из пределов равен бесконечности) задаются ур-м х=х0.
Наклонные асимптоты (р(х) - расстояние между соответствующими точками прямой y=kx+b и f(x)) задаются ур-ем y=kx+b.