Числовые множества, их границы.

Вещественное (действительное) число – любая десятичная дробь.

N – натуральные числа 1, 2…;

Z – все целые числа

Q – рациональные числа (периодические десятичные дроби)

Сегмент (отрезок, замкнутый промежуток) – множество х чисел, удовлетворяющих неравенству a £ x £ b, обозначается [a,b].

Интервал (открытое множество) – множество х чисел, удовлетворяющих неравенству a < x < b, обозначается (а, b); если a £ x <b, то это полуинтервал [a,b).

Верхней границей множ-ва А 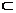R называют такое число с 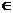R, если для всякого а 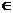А выполнено неравенство а £ с.

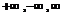3. Операции над символами бесконечности

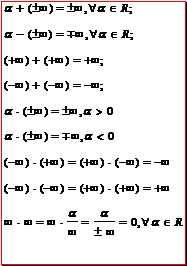
Неопределенными называются такие операции, как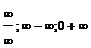
Множество А называется ограниченным сверху, если x<b.

Множество А называется ограниченным снизу, если x>b.

Множество А называется ограниченным, если оно ограничено и сверху, и снизу.

Точная верхняя граница (супремум, supA) –наименьшая из всех верхних границ.

Точная нижняя граница (инфимум, infA) – наибольшая из всех нижних границ.

Свойства модуля |x|:

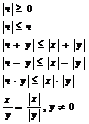
4. Понятие функции

Пусть даны два множества X и Y. Говорят, что задано отображение множеств X а во множество Y (или задана функция на Х со значениями в Y), если всякому x 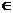X по некоторому правилу f поставлен в соответствие элемент y 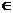Y.

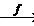f : X ®Y, x y

При этом элемент y = f(x) называют образом элемента х при отображении f.

Многозначная функция – много значений у.

Однозначная функция – одно значение у.

х – аргумент (прообраз)

у – значение функции (образ).

Функция взаимнооднозначная – если каждому значению х соответствует значение у.

Числовая последовательность – функция натурального аргумента f(n) или f:N®R.

Способы задания функции:

Явный способ – можно выразить переменную.

Неявный способ – нельзя выразить переменную.

Параметрический – каждая функция выражается через параметр.

Графический.

Табличный.

Алгоритмический.

Частные классы отображений

Класс1. Числовая функция одного числового аргумента, X 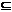R, Y 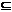R: y=f(x).

Например: y=x2, y= 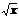, y= sinx

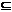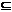Класс2. Если x = (x1, x2, …xn), то y = f(x1, x2,xn) - числовая функция векторного аргумента (или числовая функция многих скалярных переменных), X Rn, Y R.

Например: y = x 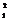+ sin (x1 + x2 ).

Класс3. X 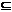R, y 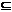Rn – f : X 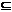R®Y 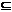Rn. – вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x из X вектор у = f(x) из Rn, т.е. каждая координата вектора f(x) есть скалярная функция скалярного аргумента х:

f (x) = [f1 (x), f2 (x), …, fn(x)]T

Класс4. X 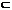Rn, Y 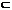Rm – вектор-функция векторного аргумента.

Полагая, что х = (x₁ , x₂, …, x_n ), у = (h₁, h₂ ,…h_m ), получим: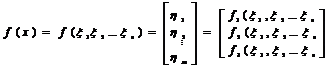

Координатные функции – функции f₁,f₂,,,,f_n в классах 3 и 4.

График функции f(x) - множество точек (x, f(x)).

В случае скалярной функции одного скалярного аргумента графиком функции f (x) является некоторая кривая.

В случае скалярной функции двух скалярных аргументов графиком f(x) является некоторая поверхность.

Монотонно возрастающей/убывающей функцией на множестве Xназывается функция f, если для любых двух точек х₁ и х₁ из Х, удовлетворяющих неравенству х₁< х₂, выполняется неравенство f(x₁) £ f(x₂) и называется строго монотонно возрастающей, если из условия

х₁< х₂ следует f(x₁) < f(x₂).

Ограниченной называется функция f если множество ее значений Y={f(x), xÎX} ограничено.

Функция f(x) называется четной, если выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси у.

Например: f(x) = х², f(x) =х⁴, f(x) = cos(x)

Функция f(x) называется нечетной, если выполняется равенство f(-x) = -f(x). График нечетной функции проходит относительно начала координат.

Например: f(x) =x³, f(x) = sin(x)

Функция называется общей, если неизвестно: четная она или нечетная.

Функция называется периодической, в которой f(x+T)=f(x), где T – период.

Например: cos (x + 2p) = cosx,

cos (wx) = cos (wx+2p) = cosw(x +2p/w)

Обратная функция – функция, противоположная данной.

Отображение функции – через заданные параметры х находим значения у.