Множества, операции над ними
Терминология
Математический анализ
Множества, операции над ними
Заданное множество – такое множество, при котором есть правило, позволяющее установить относительно любого объекта, является ли он элементом этого множества или нет.
Множество А входит в В (А – подмножество В), если для любого а 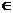 А соответствует а
А соответствует а 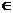 В.
В.
Множ-ва называют равными, если А 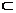 В и В
В и В 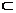 А.
А.
Расширенное множество вещественных чисел –множество |R=|R+( 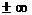 ), где
), где 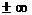 - несобственные числа.
- несобственные числа.
Операции над множествами.
Объединение или сумма множеств А и В – множество С, состоящее из всех элементов множеств А и В (А 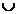 В, А +В) не содержит других элементов.
В, А +В) не содержит других элементов.
Свойства множеств:
А 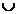 А=А, А
А=А, А 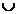 В=В
В=В 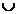 А,
А,
(А 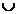 В)
В) 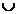 С = А
С = А 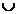 (В
(В 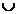 С)
С)
Пересечение множеств А и В – Множество С (С=А 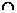 В), состоящее лишь из тех элементов, которые принадлежат одновременно А и В.
В), состоящее лишь из тех элементов, которые принадлежат одновременно А и В.
Свойства множеств:
А 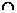 В=В
В=В 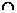 А, А
А, А 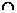 А=А
А=А
(А 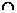 В)
В) 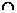 С=А
С=А 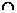 (В
(В 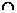 С)
С)
Разность множеств А и В – множество А\В, содержащее все те и только те элементы множества А, которые не являются элементами множества В.
Прямое (декартовое) произведение множеств А и В – множество А×В, элементами которого являются всевозможные пары (а,в), где а 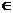 А, в
А, в 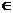 В.
В.
Частные классы отображений
Класс1. Числовая функция одного числового аргумента, X 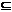 R, Y
R, Y 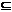 R: y=f(x).
R: y=f(x).
Например: y=x2, y= 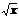 , y= sinx
, y= sinx
Класс2. Если x = (x1, x2, …xn), то y = f(x1, x2,xn) - числовая функция векторного аргумента (или числовая функция многих скалярных переменных), X 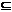 Rn, Y
Rn, Y 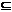 R.
R.
Например: y = x 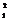 + sin (x1 + x2 ).
+ sin (x1 + x2 ).
Класс3. X 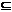 R, y
R, y 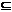 Rn – f : X
Rn – f : X 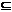 R®Y
R®Y 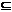 Rn. – вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x из X вектор у = f(x) из Rn, т.е. каждая координата вектора f(x) есть скалярная функция скалярного аргумента х:
Rn. – вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x из X вектор у = f(x) из Rn, т.е. каждая координата вектора f(x) есть скалярная функция скалярного аргумента х:
f (x) = [f1 (x), f2 (x), …, fn(x)]T
Класс4. X 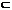 Rn, Y
Rn, Y 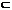 Rm – вектор-функция векторного аргумента.
Rm – вектор-функция векторного аргумента.
Полагая, что х = (x1 , x2, …, xn ), у = (h1, h2 ,…hm ), получим: 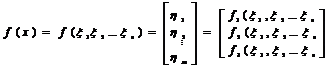
Координатные функции – функции f1,f2,,,,fn в классах 3 и 4.
График функции f(x) - множество точек (x, f(x)).
В случае скалярной функции одного скалярного аргумента графиком функции f (x) является некоторая кривая.
В случае скалярной функции двух скалярных аргументов графиком f(x) является некоторая поверхность.
Монотонно возрастающей/убывающей функцией на множестве Xназывается функция f, если для любых двух точек х1 и х1 из Х, удовлетворяющих неравенству х1< х2, выполняется неравенство f(x1) £ f(x2) и называется строго монотонно возрастающей, если из условия
х1< х2 следует f(x1) < f(x2).
Ограниченной называется функция f если множество ее значений Y={f(x), xÎX} ограничено.
Функция f(x) называется четной, если выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси у.
Например: f(x) = х2, f(x) =х4, f(x) = cos(x)
Функция f(x) называется нечетной, если выполняется равенство f(-x) = -f(x). График нечетной функции проходит относительно начала координат.
Например: f(x) =x3, f(x) = sin(x)
Функция называется общей, если неизвестно: четная она или нечетная.
Функция называется периодической, в которой f(x+T)=f(x), где T – период.
Например: cos (x + 2p) = cosx,
cos (wx) = cos (wx+2p) = cosw(x +2p/w)

Обратная функция – функция, противоположная данной.
Отображение функции – через заданные параметры х находим значения у.
Системы окрестностей
Окрестностью точки х0 из R называется любой интервал (a,b), содержащий эту точку.
Частные виды окрестностей:
Симметричная Ud(x0) точки х0 радиусом d>0,
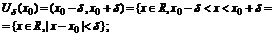
Проколотая окрестность – окрестность U(x0), из которой удалена точка х0, U(x0)={xÎR, a<x<b, x¹x0)};
Симметричная проколотая окрестность: Ud(x0)={xÎR, 0<|x-x0|<d}.
Окрестностью бесконечно удаленной точки 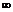 в R (U (
в R (U ( 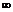 )) называется внешность некоторого отрезка, т.е. множество точек, не принадлежащих этому отрезку.
)) называется внешность некоторого отрезка, т.е. множество точек, не принадлежащих этому отрезку.
Симметричной окрестностью точки 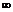 называется внешность симметричного относительно нуля отрезка.
называется внешность симметричного относительно нуля отрезка.
Окрестностью бесконечно удаленной точки в Rn(U ( 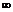 )) называется внешность шара с центром в начале координат либо внешность n – мерного куба, симметричного относительно начала координат.
)) называется внешность шара с центром в начале координат либо внешность n – мерного куба, симметричного относительно начала координат.
Предельная точка (точка сгущения) – точка М0, множества Х, если в любой ее окрестности есть хотя бы одна отличная от М0 точка множества Х.
Внутренняя точка множества Х– точка М0ÎХ, входящая в множество Х вместе с некоторой окрестностью.
Граничная точка М0 множества Х – такая точка, в окрестности которой есть точки как принадлежащие Х, так и не принадлежащие ему.
Теоремы о пределах.
1. Если предел существует, то он единственный, если пределов больше 1, то предела не существует.
2. Если существует предел Xn=a, то ограничена в окрестности точки а. (обратное нет!)
3. Всякая монотонная ограниченная последовательность имеет предел.
4. Пусть 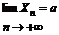 ,
, 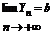 , тогда А – предел суммы:
, тогда А – предел суммы:
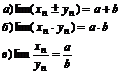
Предел вычисляется, если yn®0, предел =0, а yn¹0.
Раскрытие неопределенности.
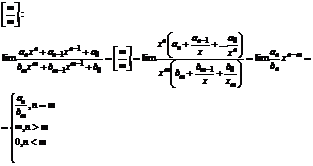
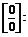
Чтобы решить пример с данной неопределенностью, необходимо максимально упростить выражение, сократить какие-либо переменные, и подставить число из предела.
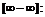
Чтобы решить пример с этой неопределенностью, мы упрощаем выражение и затем подставляем 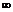 вместо неизвестной переменной. По определенным формулам ищем значение.
вместо неизвестной переменной. По определенным формулам ищем значение.
Непрерывность функций.
Непрерывной называется функция f(x) в точке x0, если предел f(x)=f(x0) при х®х0.
lim f(x)=f(x0)Ûlim f(x)=lim f(x)=f(x0)
x®x0 x®x0
lim (x0-0)=lim f(x) - предел слева
lim (x0+0)=lim f(x) – предел справа.
Непрерывной является такая функция, у которой предел слева = пределу справа.
Теорема1. Для того, чтобы функция была непрерывной в точке х0 Û чтобы она была непрерывна слева и справа в этой точке.
Теорема2. Если функции f и t непрерывны в точке х0, то и функции f+t, f*t, f/t (t(x0)¹0) тоже будут непрерывны в этой точке.
Теорема3. Для того, чтобы функция y = f(x) была непрерывна в точке х0, Û чтобы все ее координатные функции были непрерывны в х0.
Теорема4. Пусть функция f непрерывна в точке x0 и t непрерывна в точке y0. Тогда их суперпозиция (сложная функция) f 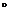 t=f(t) также непрерывна в точке х0.
t=f(t) также непрерывна в точке х0.
Теорема5. Все элементарные функции вещественного переменного непрерывны в области определения.
Теорема6. Пусть скалярная функция f скалярного переменного задана на отрезке [a,b] и f(a)=A, f(b)=B, A¹B. Если функция f непрерывна на [a,b], то для любого С, лежащего между А и В, существует точка с Î[a,b] такая, что f(c)=C.
Теорема7. Если функция y=f(x) непрерывна в замкнутой области Х и в некоторых точках, принадлежащих этой области, принимает определенные значения, неравные между собой, то для любого числа С, заключенного между этими значениями, существует точка х2 такая, что f(x2)=C.
Теорема 8 (I теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном в Rn множестве Х функция y=f(x) ограничена на этом множестве.
Теорема9 (II теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве в Rn функция f(x) принимает в нем наибольшее и наименьшее значения.
Степенная функция – функция вида f(x) = xa,a ÎR
Показательная функция – функция вида f(x) = ax, а¹1, а>0. а – const, x – переменная.
Степенно-показательная функция – функция вида f(x)=u(x)v(x).
Точка разрыва функции f(x) - точка х0 в которой нарушается непрерывность, а поэтому в этой точке нарушается одно из равенств.
Классификация точек разрыва
Существует 3 нарушения:
1. Устранимый разрыв.
Устранимым разрывом называется точка х0, если конечный предел слева равен конечному пределу справа и ¹ f(x0).
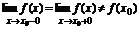
2. Разрыв I рода (неустранимый).
Точкой разрыва I рода называется точка х0, если конечные пределы 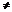 (односторонние).
(односторонние).
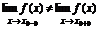 .
.
3. Разрыв II рода
Точка разрыва II рода – точка x0, при которой хотя бы один из односторонних пределов = 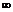 или не существует.
или не существует.
Замечательные пределы.
Первый замечательный предел и его следствия.
 - Первый замечательный предел.
- Первый замечательный предел.
Следствия:
Þ1. 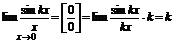
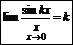
Þ2. 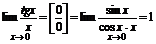
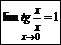
Þ3.
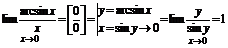
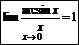
Главная часть б.м.
Главная часть б. м. - простейшая б.м. a(х) ~б.м. b(х).
т.е. если 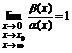 , то a(х) – главная часть b(х)
, то a(х) – главная часть b(х)
Простейшие б.м:
При х®0, a(х)=схk
При х®х0,a(х)=с(х-х0)k
При х®¥, 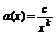
Сравнение б.м.
Сравнимыминазываются б.м. функции a(х) и b(х) при х=х0, если существует хотя бы один из пределов 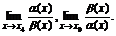
Порядком малости – называется вещественное число k (kÎR, k>0) a(х) относительно b(х), если
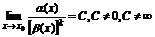
Чем больше порядок малости, тем скорость выше.
Правило сравнения б.м:
Пусть a(х) и b(х) б.м. при х®х0 и пусть 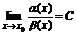 , тогда если:
, тогда если:
1. С=0, тогда a имеет более порядок малости, чем b, т.е. ее скорость выше: a=0(b)
2. С= 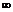 , тогда b=0a.
, тогда b=0a.
3. С¹0, С¹¥, тогда (a=С(b)) a и b имеют одинаковый порядок малости.
4. С=1, то a и b называют эквивалентными б.м. (a~b).
5. С не сущ., то б.м. несравнимы.
Сравнение б.б.
Функция f(x) называется б.б. при х®х0, если предел этой функции равен +¥,-¥, ¥.
Правило сравнения б.б.
Пусть f(x) и 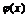 - б.б. при х®х0 и
- б.б. при х®х0 и 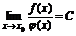 , тогда если:
, тогда если:
С=¥, то f(x) имеет более высокий порядок роста.
С=0, то 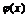 имеет более высокий порядок роста.
имеет более высокий порядок роста.
С¹0, С¹¥, то порядок роста одинаковый.
С=1, то f(x) ~ 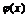 .
.
Если предел не сущ., то f(x) и 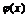 несравнимы.
несравнимы.
Замечания:
Если б.б. представляет собой сумму слагаемого разного порядка роста, то она эквивалентна слагаемому наивысшего порядка роста.
При вычислении пределов в произведении, частном б.б. можно заменять эквивалентными.
Таблица эквивалентных б.м.
б.м. при х®х0 или х® ¥, ±¥:
sinx~x 7. ax – 1~xlna,a>0,a¹1 sinkx~kx 8. ex-1~x arcsinx~x 9. ln(1+x) ~x tgx~x 10. (1+x)k – 1 ~kx arctgx~x 11. 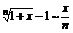 loga(1+х) ~(logae)(x) 12. loga(1+х) ~(logae)(x) 12. 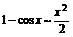 |
В разности эквивалентом заменять нельзя!!!
Например:
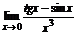 нельзя заменить tgx и sinx на х.
нельзя заменить tgx и sinx на х.
Понятие производной.
Производная функции f(x) в точке Х0 – предел отношения приращения функции к приращению аргумента (Dх®0):
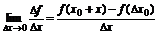 .
.
Конечный предел – производная функции в точке х0. Обозначается: f’(x0), y’(x0), 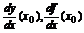 .
.
Таблица производных.
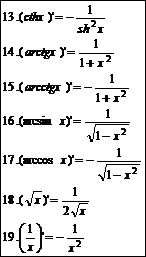
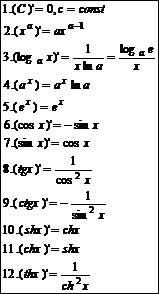
Частная производная функции f(x1,x2,…,xn) по переменной х1 – предел
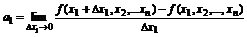 , обозначается:
, обозначается:
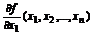
Смешанные частные производные – частные производные, в которые входит дифференцирование по различным переменным.
Правило дифференцирования:
Пусть функция v(x) и u(x) дифференцируемы в точке х, тогда в этой точке существует производная.
Свойства производных:
1. (u(x)±v(x))’=v’(x)±v’(x)
2. (u(x)  v(x))’=u’(x)*v(x)+v’(x)*u(x)
v(x))’=u’(x)*v(x)+v’(x)*u(x)
3. 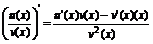
Правило дифференцирование обратной функции:
Обратная функция x = f-1– функция, заданная неявно уравнением f(x)-y =0.
Если у=f(x) монотонная функция, то существует x=j(y) на Y.
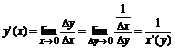
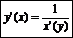
Производная по направлению.
Пусть даны скалярная функция f(M)=f(x1,x2,…,xn) векторного аргумента, ненулевой вектор а и фиксированная точка М0.
Тогда производной от функции f(M) в направлении вектора ав точке М0 называется предел 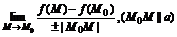
и обозначается 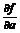 , при этом знак выбираем знак «+», если вектор M0Ma,
, при этом знак выбираем знак «+», если вектор M0Ma,
« - », если M0M¯a.
Кривизна графика фун-и в точке М0 – число k, определяемое равенством 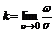 ,
,
Где w- угол между касательными в точках М и М0,
а s - длина дуги.
Дифференциал функции.
Дифференциал высшего порядка
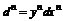
33. Формула Тейлора.
Если f – скалярная фун-я одной или многих переменных, имеющая непрерывные производные до порядка (n+1) включительно, то ее приращение в точке х0, вызванное приращением аргумента Dх, можно представить в виде:
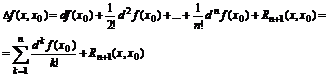 Эта формула применяется для вычисления приближенных значений.
Эта формула применяется для вычисления приближенных значений.
Формула Лагранжа.
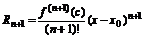 , где с – точка, лежащая между х и х0.
, где с – точка, лежащая между х и х0.
Формула Маклорена.
При х=х0 формула Тейлора называется формулой Маклорена.
Теорема1.
Пусть функция f имеет в точке х0 конечную производную f’(x0).
Если f’(x0)>0 то существует окрестность U(x0) этой точки такая, что f(x)>f(x0) для любого х Î U+(х0) (из правосторонней окрестности).
f(x)<f(x0) для любого х Î U-(х0) (из левосторонней окрестности).
При f’(x0)<0 выполняются противоположные неравенства.
Точка наибольшего или наименьшего значения функции f(x) в области Х – точка х0 (хÎХ), для всех хÎХ которых выполняется неравенство:
f(x)£f(x0) (f(x)³f(x0).
Теорема Ферма. Пусть фун-я f(x) определена на промежутке (a,b) и в точке с этого промежутка принимает наибольшее или наименьшее значения. Тогда, если существует f’(c), то f’(c)=0.
Теорема Ролля. Если:
1) f(x) определена и непрерывна на отрезке [a,b]
2) существует конечная производная f’(x) на (а,b)
3) f(a)=f(b), то существует такая точка с, a<c<b что f’(c)=0.
Теорема Лагранжа.Если:
1) f(x) определена и непрерывна на отрезке [a,b]
2) существует конечная производная f’(x) на (a,b),то найдется такая точка с, a<c<b, что
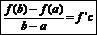
Теорема Коши. Если:
1) функции f(x) и g(x) определены и непрерывны на [a,b]
2) существуют конечные производные f’(x) и g’(x) на (a,b)
3) g’(x)¹0 для всех х Î (a,b),
то существует точка с Î (a,b) такая, что 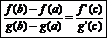
Теорема6. Если функция f(x) имеет в точке х конечную производную f’(x), то фун-я f дифференцируема в этой точке.
Теорема7. Если функция f(x) имеет в то х конечную производную и эта производная непрерывна в этой точке, то функция f дифференцируема в этой точке.
Правило Лапиталя.
Если:
1) функции f(x) и g(x) определены на (a,b)
2) 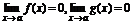
3) всюду на (a,b) существуют производные f’(x) и g’(x) причем g’(x)¹0
4) существует предел 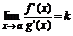 , то существует и предел
, то существует и предел 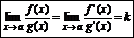
Теорема Лапиталя2. Если:
1) функции f(x) и g(x) определены на (a,b)
2) 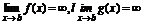
3) всюду на (a,b) существуют производные f’(x) и g’(x), причем g’(x)¹0
4) существует предел 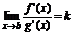 , то существует и предел
, то существует и предел 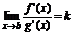 .
.
Выпуклость графика функции.
Выпуклым вверх (вниз) называется график функции, если все точки любой дуги графика лежат выше (ниже) хорды, соединяющей ее концы.
Теорема1. Если функция f(x) определена, непрерывна на [a,b] и имеет конечную производную на (a,b), то для того, чтобы график фун-и f(x) был выпуклым вверх (вниз), необходимо и достаточно, чтобы производная f’(x) убывала (возрастала).
Теорема2. Пусть f(x) определена на [a,b] и существует вторая производная f’’(x) на (a,b). Тогда для выпуклости вверх (вниз) графика функции необходимо и достаточно, чтобы было f’’(x)£0 (f’’(x)³0) на (a,b).
Точка перегиба графика функции, непрерывной в х0 – точка х0 перехода от выпуклости вниз к выпуклости вверх или наоборот.
Асимптоты графикафункции.
Асимптота – прямая L графика функции f(x), если при стремлении точки графика к бесконечности расстояние между точкой графика фун-и и прямой L стремится к нулю.
Вертикальные асимптоты (если хотя бы один из пределов равен бесконечности) задаются ур-м х=х0.
Наклонные асимптоты (р(х) - расстояние между соответствующими точками прямой y=kx+b и f(x)) задаются ур-ем y=kx+b.


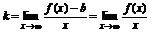
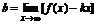
Формулы
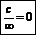
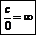
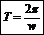
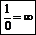 хn=n!
хn=n!
0!=1
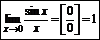 |
Первый замечательный предел:
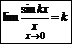 Следствия:
Следствия:
Þ1. 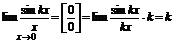
Þ2. 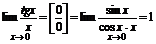
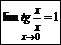
Þ3.
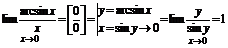
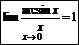
Второй замечательный предел:
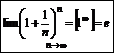 - n – для натуральных чисел
- n – для натуральных чисел
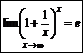 - х – для любых чисел
- х – для любых чисел
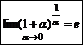 -
- 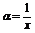
Следствия:
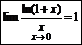
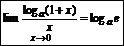 Þ1
Þ1
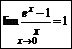
Þ2
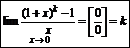 |
Þ3
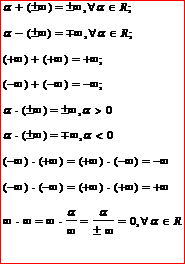 Операции над символами бесконечности:
Операции над символами бесконечности:
Таблица эквивалентных б.м.:
sinx~x 7. ax – 1~xlna,a>0,a¹1 sinkx~kx 8. ex-1~x arcsinx~x 9. ln(1+x) ~x tgx~x 10. (1+x)k – 1 ~kx arctgx~x 11. 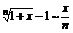 loga(1+х) ~(logae)(x) 12. loga(1+х) ~(logae)(x) 12. 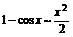 |
Таблица производных:
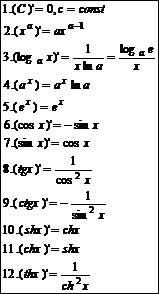 | 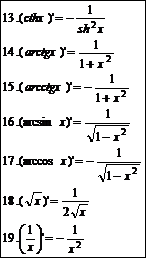 | ||
Свойства производных:
1. (u(x)±v(x))’=v’(x)±v’(x)
2. (u(x)  v(x))’=u’(x)*v(x)+v’(x)*u(x)
v(x))’=u’(x)*v(x)+v’(x)*u(x)
3. 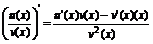
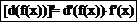 производная сложной функции:
производная сложной функции:
Производная функции, заданной параметрически:
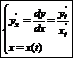
Формула Тейлора:
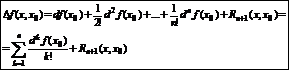
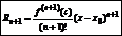 |
Формула Лагранжа:
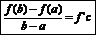 |
Теорема Лагранжа:
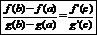 |
Теорема Коши:
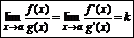 |
Правило Лапиталя:
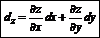 |
Полный дифференциал:
Полный дифференциал – сумма частных дифференциалов:
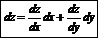 |
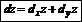
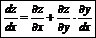 | 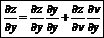 |
Дифференцирование сложных функций:
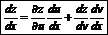
Дифференцирование неявных функций:
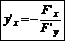 в точке М0
в точке М0
Производные дифференциала высшего порядка:
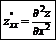 | 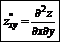 | 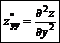 | |||
повторные смешанные
производные производные
Если смешанные производные непрерывны, они всегда равны.
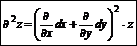
производная по направлению: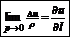
43. Содержание
1. Множества, операции над ними. 3
2.Числовые множества, их границы. 4
3. Операции над символами бесконечности. 5
4. Понятие функции. 7
5. Частные классы отображений. 8
6.Класс основных элементарных функций. 10
7. Суперпозиция (композиция отображений) 11
8. Системы окрестностей. 11
9. Предел последовательности (определение Коши) 12
10.Определение предела функции на языке последовательностей (определение Гейне). 13
11. Теоремы о пределах. 14
12. Раскрытие неопределенности. 14
13. Непрерывность функций. 15
14. Классификация точек разрыва. 17
15. Замечательные пределы. 18
16. Второй замечательный предел и его свойства. 19
18. Главная часть б.м. 22
19. Сравнение б.м. 22
20. Сравнение б.б. 23
21. Свойства эквивалентных бесконечно малых функций. 24
22. Таблица эквивалентных б.м. 25
23. Понятие производной. 26
24. Физический, геометрический и экономический смысл производной. 26
25. Таблица производных. 28
26. Производная сложных функций. 30
27. Производная высшего порядка. 31
28. Дифференцирование функций, заданных неявно. 31
29. Дифференцирование параметрически заданных функций. 31
30. Производная по направлению. 32
31. Уравнение касательной плоскости и нормали к поверхности. 32
32. Дифференциал функции. 34
33. Формула Тейлора. 35
34. Формула Лагранжа. 35
35. Формула Маклорена. 35
36. Основные теоремы дифференциального исчисления. 35
37. Условия постоянства функции. 38
38. Достаточные условия экстремума. 38
39. Выпуклость графика функции. 39
40. Асимптоты графикафункции. 40
41. Общая схема исследования функции. 41
42. Формулы. 42
Терминология
Математический анализ
Множества, операции над ними
Заданное множество – такое множество, при котором есть правило, позволяющее установить относительно любого объекта, является ли он элементом этого множества или нет.
Множество А входит в В (А – подмножество В), если для любого а 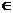 А соответствует а
А соответствует а 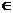 В.
В.
Множ-ва называют равными, если А 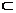 В и В
В и В 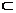 А.
А.
Расширенное множество вещественных чисел –множество |R=|R+( 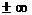 ), где
), где 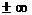 - несобственные числа.
- несобственные числа.
Операции над множествами.
Объединение или сумма множеств А и В – множество С, состоящее из всех элементов множеств А и В (А 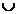 В, А +В) не содержит других элементов.
В, А +В) не содержит других элементов.
Свойства множеств:
А 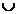 А=А, А
А=А, А 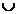 В=В
В=В 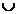 А,
А,
(А 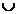 В)
В) 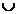 С = А
С = А 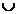 (В
(В 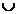 С)
С)
Пересечение множеств А и В – Множество С (С=А 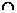 В), состоящее лишь из тех элементов, которые принадлежат одновременно А и В.
В), состоящее лишь из тех элементов, которые принадлежат одновременно А и В.
Свойства множеств:
А 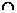 В=В
В=В 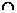 А, А
А, А 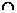 А=А
А=А
(А 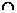 В)
В) 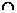 С=А
С=А 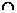 (В
(В 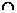 С)
С)
Разность множеств А и В – множество А\В, содержащее все те и только те элементы множества А, которые не являются элементами множества В.
Прямое (декартовое) произведение множеств А и В – множество А×В, элементами которого являются всевозможные пары (а,в), где а 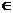 А, в
А, в 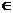 В.
В.
