Геометрический смысл условий монотонности.
Известно: 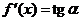 – геометрический смысл производной (
– геометрический смысл производной ( 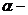 угол между касательной и осью
угол между касательной и осью 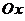 ).
).
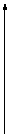 |  | ||||
 | |||||
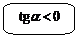
 y y
y y
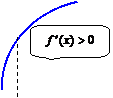 | |||||||
 | |||||||
 | |||||||
 | |||||||

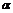
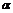

 O x0 x O x0 x
O x0 x O x0 x
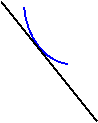
Функция возрастает: 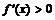 , так как касательная наклонена к оси , так как касательная наклонена к оси 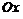 под острым углом под острым углом 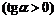 . . | Функция убывает: 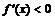 , так как касательная наклонена к оси , так как касательная наклонена к оси 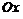 под тупым углом под тупым углом 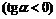 . . |
Практическое правило для нахождения промежутков монотонности функции. Для нахождения промежутков монотонности функции достаточно
1) разбить область существования функции  на интервалы точками, в которых ее первая производная
на интервалы точками, в которых ее первая производная 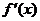 равна нулю или не существует,
равна нулю или не существует,
2) определить ее знак в каждом из этих интервалов. Для чего достаточно вычислить значение производной в какой-либо одной точке каждого интервала, ибо внутри каждого интервала производная 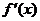 сохраняет постоянный знак (или решить неравенства
сохраняет постоянный знак (или решить неравенства 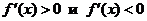 ).
).
Пример 1. Определить промежутки монотонности функции 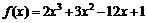 .
.
▲ Функция определена на всей числовой оси 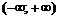
Найдем ее первую производную: 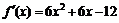 . Она определена на всей числовой оси и равна нулю в точках
. Она определена на всей числовой оси и равна нулю в точках 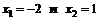 (решается уравнение
(решается уравнение 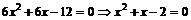 ).
).
Эти точки разбивают область определения функции на интервалы 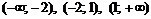 .
.
Определим знак производной в каждом из интервалов, для чего достаточно вычислить знак 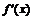 в какой-либо одной точке каждого интервала. Для первого интервала удобно взять
в какой-либо одной точке каждого интервала. Для первого интервала удобно взять 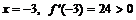 , следовательно, в интервале
, следовательно, в интервале 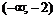 функция возрастает. Для второго интервала удобно взять
функция возрастает. Для второго интервала удобно взять 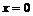 ,
, 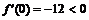 , следовательно, в интервале
, следовательно, в интервале 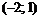 функция убывает. Для третьего интервала
функция убывает. Для третьего интервала 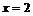 ,
, 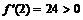 , следовательно, в интервале
, следовательно, в интервале 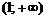 функция возрастает.
функция возрастает.
Результаты исследования приведены в таблице.
Интервал изменения  | 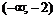 | 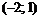 | 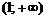 | ▼ |
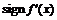 | + | – | + | |
Поведение функции 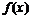 |  |  |  |
Замечание. Условимся в дальнейшем возрастание, убывание функции на интервале обозначать так:  .
.
Пример 2. Определить промежутки монотонности функции 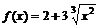 .
.
▲ Функция определена на всей числовой оси 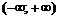
Найдем ее первую производную: 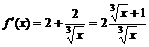 . Производная не существует
. Производная не существует 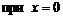 и равна нулю
и равна нулю 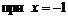 .
.
Этими точками разобьем область существования функции на интервалы 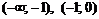 ,
, 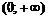 .
.
Для определения знака производной в каждом интервале удобно взять точки 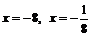 и
и 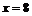 . Тогда
. Тогда 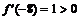 , следовательно, на интервале
, следовательно, на интервале 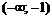 функция возрастает;
функция возрастает; 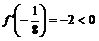 , значит, на интервале
, значит, на интервале 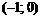 функция убывает;
функция убывает; 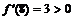 , значит, на интервале
, значит, на интервале 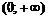 функция возрастает.
функция возрастает.
Интервал изменения  | 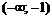 | 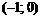 | 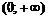 | ▼ |
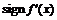 | + | – | + | |
Поведение функции 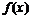 |  |  |  |
Пример 3. Определить промежутки монотонности функции 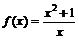 .
.
▲ Функция не определена 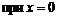 , т. е. область определения функции
, т. е. область определения функции 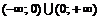 .
.
Найдем ее первую производную: 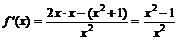 . Производная не существует
. Производная не существует 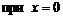 и равна нулю
и равна нулю 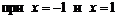 .
.
Этими точками разобьем область существования функции на интервалы 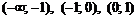 ,
, 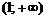 .
.
Для определения знака производной в каждом интервале удобно взять точки 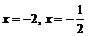 ,
, 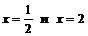 . Тогда
. Тогда 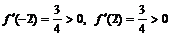 , следовательно, на интервалах
, следовательно, на интервалах 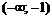 и
и 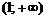 функция возрастает;
функция возрастает; 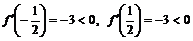 , следовательно, на интервалах
, следовательно, на интервалах 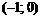 и
и 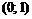 функция убывает.
функция убывает.
Интервал изменения  | 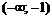 | 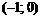 | 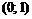 | 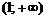 | ▼ |
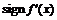 | + | – | – | + | |
Поведение функции 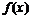 | 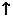 | 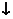 | 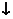 |  |
ЭКСТРЕМУМЫ ФУНКЦИИ
Рассмотрим функцию  , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки  , включая и саму точку
, включая и саму точку  .
.
Определение 3. Точка  называется точкой локального максимума, а значение функции в ней – локальным максимумом функции
называется точкой локального максимума, а значение функции в ней – локальным максимумом функции  , если существует такое
, если существует такое 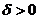 , что для всех
, что для всех 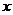 , удовлетворяющих условию
, удовлетворяющих условию 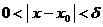 , верно неравенство
, верно неравенство 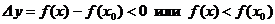 .
.
Определение 4. Точка  называется точкой локального минимума, а значение функции в ней – локальным минимумом функции
называется точкой локального минимума, а значение функции в ней – локальным минимумом функции  , если существует такое
, если существует такое 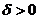 , что для всех
, что для всех 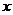 , удовлетворяющих условию
, удовлетворяющих условию 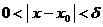 , верно неравенство
, верно неравенство 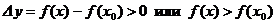 .
.
Точки локального максимума и минимума называются точками локального экстремума, а значения в них – локальными экстремумами функции.
Необходимое условие существования точек экстремума функции.
Теорема 2.1. Для того чтобы точка  была точкой экстремума функции
была точкой экстремума функции  , определенной в окрестности этой точки, необходимо выполнение одного из двух условий: либо
, определенной в окрестности этой точки, необходимо выполнение одного из двух условий: либо 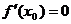 ; либо производная
; либо производная 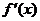 не существует в точке
не существует в точке  (в частности, где
(в частности, где 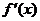 – бесконечно большая функция).
– бесконечно большая функция).
Такие точки называются критическими, и они являются точками, подозрительными на экстремум.
Достаточные условия экстремума.
I. Теорема 2.2. Пусть функция  , определенная в окрестности точки
, определенная в окрестности точки  , непрерывная в самой этой точке и дифференцируемая в некоторой
, непрерывная в самой этой точке и дифференцируемая в некоторой 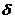 – окрестности точки
– окрестности точки  . Тогда справедливы следующие заключения:
. Тогда справедливы следующие заключения:
1) если 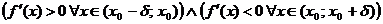 (т. е. при переходе
(т. е. при переходе 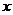 через критическую точку
через критическую точку  производная меняет знак с плюса на минус), то
производная меняет знак с плюса на минус), то  – точка локального максимума функции
– точка локального максимума функции  ;
;
2) если 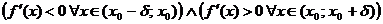 (т. е. при переходе
(т. е. при переходе 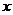 через критическую точку
через критическую точку  производная меняет знак с минуса на плюс), то
производная меняет знак с минуса на плюс), то  – точка локального минимума функции
– точка локального минимума функции  ;
;
3) если 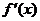 во всей
во всей 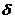 – окрестности точки
– окрестности точки  имеет один и тот же знак, то в точке
имеет один и тот же знак, то в точке  экстремума функции
экстремума функции  .
.
II. Теорема 2.3. Пусть функция  , определенная в окрестности точки
, определенная в окрестности точки  , имеет производные до 2-го порядка включительно. Если
, имеет производные до 2-го порядка включительно. Если 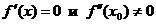 , то функция
, то функция  имеет в точке
имеет в точке  экстремум, а именно:
экстремум, а именно:
1) минимум, если 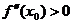 ,
,
2) максимум, если 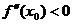 .
.
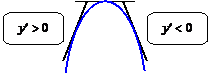
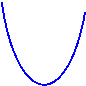 Геометрический смысл необходимых и достаточных условий экстремумов
Геометрический смысл необходимых и достаточных условий экстремумов
 |  | ||||
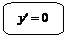 | |||||
y y
 | |||
 |

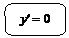

 O x O x
O x O x
Проследите за изменением производной в зоне 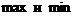 :
:
I. Слева функция возрастает, т. е. 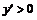 . В точке . В точке 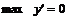 . Справа функция убывает, т. е. . Справа функция убывает, т. е. 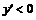 . . | I. Слева функция убывает, т. е. 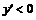 . В точке . В точке 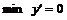 . Справа функция возрастает, т. е. . Справа функция возрастает, т. е. 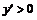 . . | |
II. 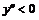 | II. 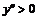 |
