Показательное (экспоненциальное распределение)

Показательным называют распределение непрерывной случайной величины Х которое описывается следующей дифференциальной функцией

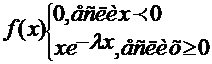
Экспоненциальное распределение для непрерывных случайных величин является аналогом распределения Пуассона для дискретных случайных величин и имеет следующий вид.

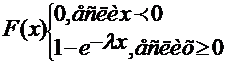
вероятность попадания случайной величины Х на интервал (α;β)

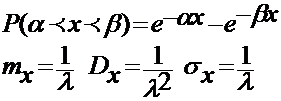
Следует отметить, что время безотказной работы удовлетворяется именно показательному закону, а поэтому это понятие часто используется в понятии надежности.

Нормальный закон распределения (закон Гаусса)

Нормальным называется распределение случайной величины Х если ф-ция плотности распределения

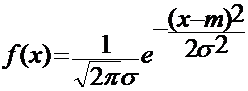
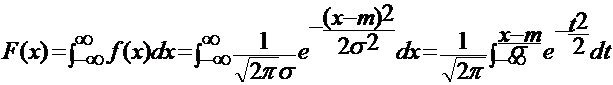
Полученное выражение через элементарные функции не может быть выражено, такая функция так называемый интеграл вероятности для которой составлены таблицы, чаще всего в качестве такой функции используют

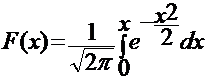
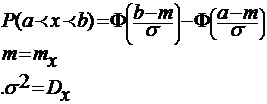
Часто по условию задачи необходимо определить вероятность попадания случайной величины Х на участок симметричный математическому ожиданию.

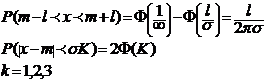
Правило трех сигм это правило часто используется для подтверждения или отбрасывания гипотезы о нормальном распределении случайной величины.

Мат. статистика

Выборочная сумма:

.

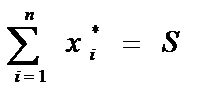Выборочное среднее:

.

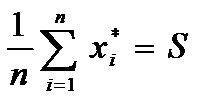Выборочная дисперсия:

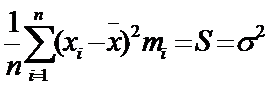, где т_i – частота.

Выборочное СКО:

.

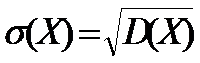Эмпирическая функция распределения:

F^*(x)=P(X<x)

F^*(x)= .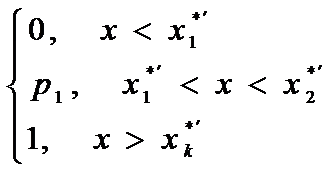

Точечные оценки:

Несмещенная оценка генеральной средней (мат.ожидания):

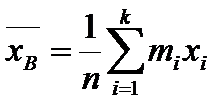, х_i – варианта выборки, m_i – частота варианты х_i, 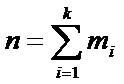- объем выборки.

Смещенная оценка генеральной дисперсии– выборочная дисперсия:

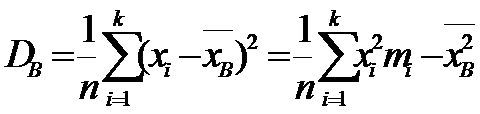, так как

.

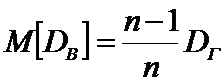Несмещенной оценкой генеральной дисперсии служит «исправленная дисперсия»:

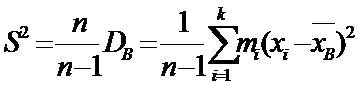. При п<30.

Коэффициент вариации:

.

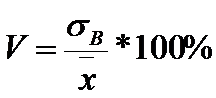Центральный момент к-го порядка:

.

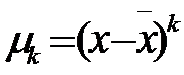Начальный момент к-го порядка:

.

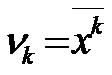Ассиметрия: 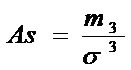, т₃=

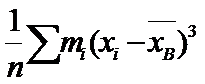
Эксцесс: 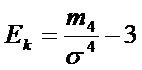, где т₄=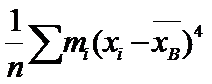

Групповая средняя: .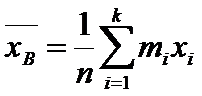

Общая средняя: 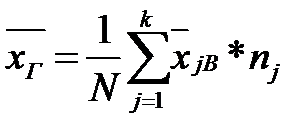, где .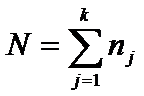

Общая дисперсия: .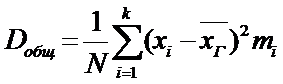

Интервальные оценки:

Доверительный интервал для мат.ожидания а нормально распределенного количества признака Х :

.

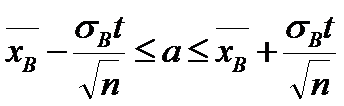Критерий согласия Пирсона:

Если число наблюдений очень велико, то закон распределения СВ не зависит от того, какому закону подчинена генеральная совокупность. Он приближается к распределению 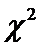с к степенями свободы, а сам критерий называется критерием согласия Пирсона:

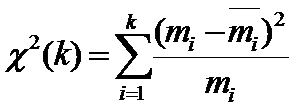, где к – количество интервалов сгруппированного ряда, т_i>0,05n.

Количество степеней свободы: r=k-p-1, где к – количество интервалов, р – количество параметров закона.

Уровень значимости α:

α=0,05 и α=0,01.

Если 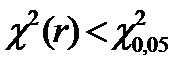, то Н₀ принимается, т.е. предполагаемый закон распределения отвечает эмпирическим данным. При этом мы ошибаемся в 5-ти случаях из 100, принимая возможно ошибочную гипотезу (ошибка 2-го рода).

Если 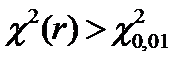, то Н₀ отвергается, т.е. предполагаемый закон не отвечает эмпирическим данным. При этом мы ошибаемся в 1-ом случае из 100, отбрасывая правильную гипотезу (ошибка 1-го рода).

Если 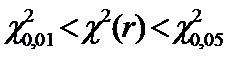, то имеем неопределенность и можно использовать др. критерии.

Корреляция

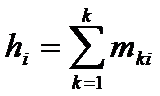- сумма частот в i-ом столбце;

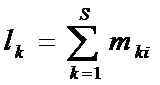- сумма частот в к-ой строке;

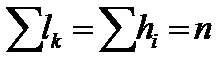- число пар (х_i ; y_k).

Условное среднее: .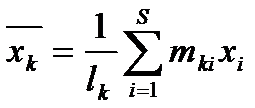

Теоретические уравнения линий регрессии:

.

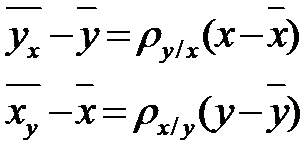Расчет числовых характеристик:

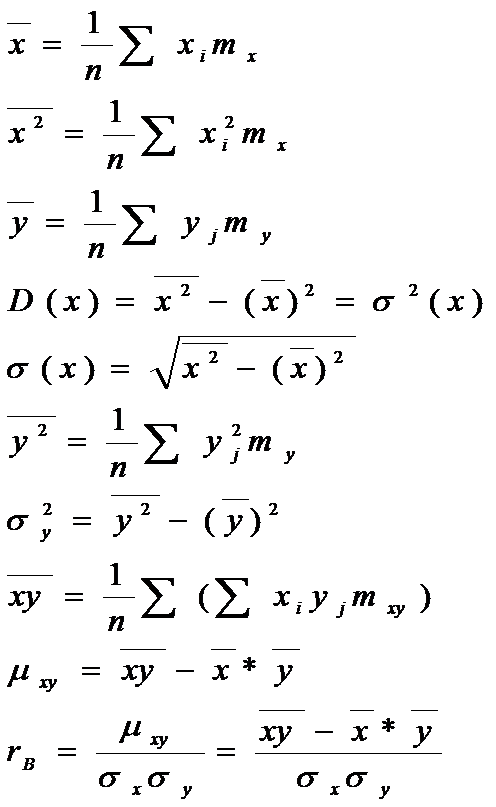
Показатель тесноты корреляционной связи – эмпирическое корреляционное отношение:

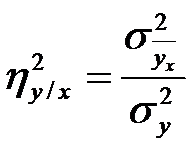, где .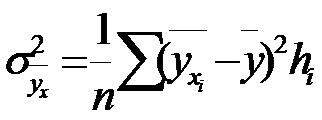

.

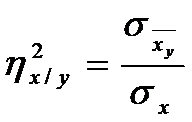Свойства:

1. 0≤η≤1.

2. если η=1, то у(х) – связь функциональная.

3. η=0, то связи нет.

4. η≥ .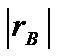

5. если η= 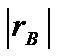, то имеет место точная линейная корреляционная зависимость.

6. чем ближе η к 0, тем корреляционная связь слабее, чем ближе к 1, тем корреляционная связь сильнее и в пределе она превращается в функциональную зависимость.

Коэффициент корреляции:

.

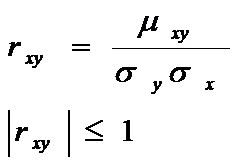Проверка значимости параметров корреляционной зависимости:

1. Проверка существенности линейной корреляционной связи (значимости регрессии).

При больших объемах выборки коэф.корреляции подчиняется нормальному закону. При этом .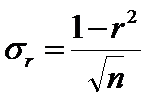

2. Проверка значимости регрессии:

.

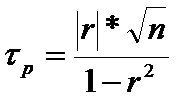Если τ_р>2,58, то с уверенностью 99% можно утверждать, что корреляционная зависимость существенна (регрессия значима). Т.е. корреляционная связь существует не только в выборке, но и во всей генеральной совокупности.

τ_р<1,96, то с уверенностью 95% можно утверждать, что корреляционная зависимость не явл. существенной, т.е. она характерна только для данной выборки и может не существовать в генеральной совокупности.

1,96<τ_р< 2,58 – несущественная корреляционная зависимость.

3. Проверка линейности выбранной модели (проверка адекватности):

.

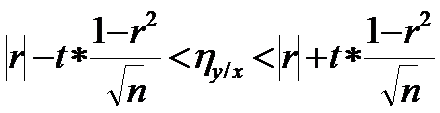Р=99% (α=0,01): t=2,58

Р=95% (α=0,05): t=1,96

Если величина η_у/х удовлетворяет этому неравенству, то выбранная модель адекватна, она соответствует эмпирическим данным.

Критерий Фишера:

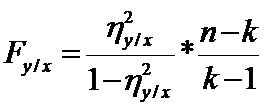, п – число наблюдений, к – число интервалов по Х.

При уровнях значимости:

α=0,05 и α=0,01: F_0,05(k-1;n-1); F_0,01(k-1;n-k).

Если F_y/x<F_0,05, то регрессия значима. Корреляционная зависимость несущественна.

Проверка значимости регрессии:

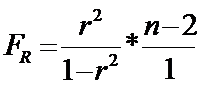, по табл. F_0,01(1;n-2), F_0,05(1;n-2).

Если F_R>F_0,01, то регрессия значима, если F_R<F_0,05, то корреляционная зависимость несущественна. Если F_0,05<F_R<F_0,01, то регрессия не явл значимой.

Адекватность модели по Фишеру:

.

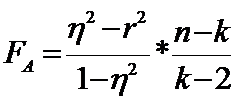F_0,01(k-2;n-k), F_0,05(k-2;n-k).

Если F_A>F_0,01, то модель неадекватна, если F_A<F_0,05, то модель адекватна.

Критерий Романовского:

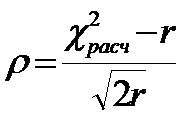, где r – число ступеней свободы. Если ρ<3, то расхождение между теоретическими и эмпирическими распределениями нужно считать незначительными.

Критерий согласованности Калмагорова:

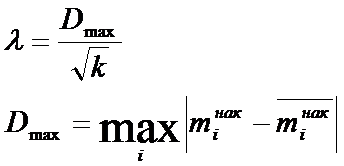- наибольшая по абсолютной величине разность между накопленными частотами эмпирического и теоретического распределения.

к – количество интервалов.

По таблице находим соответствующее значение вероятности Р(λ). Если Р(λ)<0,05, то расхождение между распределениями существенно, оно не может быть вызвано случайными причинами. Чем ближе эта вероятность к 1, тем лучше теоретическое распределение согласовывается с эмпирическим.