Вероятностная схема Бернулли

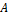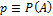Имеется опыт G, который имеет два исхода: (успех) и (неудача). Обозначим и 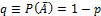. Исход G не зависит от предыдущих испытаний. G повторяется 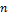раз (имеется последовательность независимых испытаний), тогда вероятность того, что в 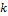испытанийиз 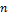произойдёт успех:

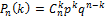
Это называется формулой Бернулли или биномиальным распределением.

Наивероятнейшее число в распределении Бернулли

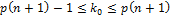
Где 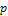— вероятность успеха, 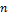— число испытаний, 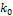— число, для которого формула Бернулли достигает наибольшего значения.

Полиномиальное распределение

Пусть результатом опыта может быть одно из 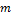независимых событий 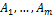, причём 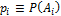. Вероятность того, что в серии из 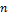независимых испытаний событие 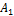произойдёт 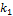раз, … , событие 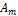произойдёт 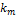раз определяется полиномиальным распределением вероятности:

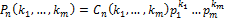
Гипергеометрическое распределение

Дано 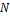объектов, из которых M помеченных. Извлекается 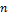объектов наугад, при этом извлечённые объекты не возвращаются. Вероятность того, что 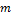из них помечены, определяется гипергеометрическим распределением:

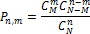
Асимптотика Пуассона

Возьмём вероятностную схему Бернулли (серия одинаковых опытов с исходом успех или неудача). Рассмотрим её при условии, что число опытов 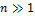, а вероятность успеха 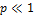, тогда можно воспользоваться упрощённой формулой (формулой Пуассона) для приблизительного вычисления вероятности того, что в 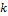случаях из 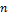будет успех:

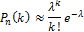
Где 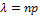. При :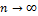

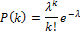
Наивероятнейшее число распределения Пуассона

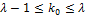
Где 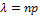, 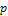— вероятность успеха, 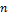— число испытаний, 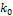— число, для которого формула Пуассона достигает наибольшего значения.

Вероятность появления событий потока

Для стационарного ординарного потока с независимыми значениями вероятность появления 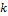событий за время :

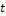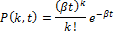
Где 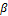— интенсивность потока.

Для ординарного потока с независимыми значения (пуассоновский поток):

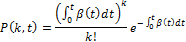
Локальная теорема Муавра-Лапласа

Возьмём вероятностную схему Бернулли (серия одинаковых опытов с исходом успех или неудача). Рассмотрим её при условии, что число опытов 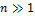, число успехов 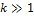, 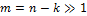.Тогда можно воспользоваться упрощённой формулой (асимптотика Муавра-Лапласа) для приблизительного вычисления вероятности того, что в 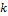случаях из 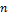будет успех:

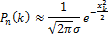
Где:

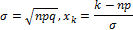
Теорема Муавра-Лапласа:

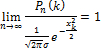
Где 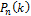— формула Бернулли.

Интегральная теорема Муавра-Лапласа

Возьмём вероятностную схему Бернулли (серия одинаковых опытов с исходом успех или неудача). Рассмотрим её при условии, что число опытов 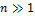, число успехов 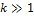, 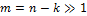. Тогда можно найти вероятность того, что число успехов будет :

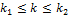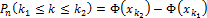
Где 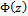— функция Лапласа:

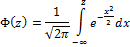
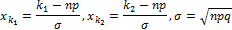
Случайные величины

Функция распределения вероятностей

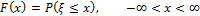
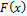— вероятность того, что случайная величина 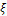окажется меньше либо равна .

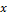Свойства:

1.

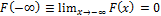
2.

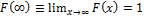
3.

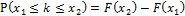
4. Функция 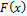неубывающая

5. Функция 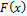непрерывна справа в каждой точке