Получение и анализ поляризованного света.

В силу упорядоченного строения кристаллы обладают некоторыми свойствами. В частности существуют кристаллы, способные некоторым образом упорядочивать электромагнитные волны.

Призма Николя – поляризатор из двух кристаллов, склеенных особым образом. Пусть у нас есть некоторый неполяризованный пучок света. Тогда, при прохождении через поляризатор Николя, у всех этих неупорядоченных кусков электромагнитных волн останутся лишь те составляющие, которые сонаправлены с некоторым выделенным направлением в призме Николя.

В лампочке каждый атом спирали выделяет кусок волны со случайными параметрами. Но в призме Николя они некоторым образом упорядочиваются и становятся сонаправлены.

Рассмотрим систему из двух призм Николя. Каждая из этих двух призм имеет своё особое направление. Пусть призма, через которую свет проходит сначала называется поляризатор, а вторая – анализатор.

Тогда возможны три случая расположения выделенных направлений поляризатора и анализатора:

1) Пусть особые направления сонаправлены. Тогда за исключением частичного поглощения второго поляризатора ничего не изменится.

2) Пусть направления перпендикулярны, тогда всё поглотится, т.к. после поляризатора на анализатор придут лишь перпендикулярные выделенному направлению анализатора волны.

3) Промежуточный случай: т.е. между выделенными направлениями некоторый угол. Тогда Очевидно, что будет иметь место следующее соотношение: .

Для определения поляризованности света нужен поляризатор.

Пусть есть некоторый свет, поляризованный некоторым образом, т.е. . Пусть он упал на границу раздела двух сред под углом Брюстера , тогда отражённая волна стала .

При отражении в общем случае изменяется плоскость поляризации.

От лампочки мы получаем следующий вид волны , где a и b – некоторые случайные величины, т.е. в каждый момент времени поступают различные .

Но после попадания на границу раздела двух сред под углом Брюстера имеем , т.е. теперь . Т.е. при отражении обычного света под углом Брюстера мы получили поляризованный свет.

Квантовые соотношения при отражении преломления.

Пусть , т.е. волна идёт например из воздуха в стекло. При этом . Рассмотрим два возможных варианта:

При . Тогда , . Тогда - имеют одинаковые знаки, т.е. коллениарны.

При . Тогда , . Тогда - имеют разные знаки, т.е. антиколлениарны.

Интерференция волн.

Пусть есть две электромагнитные волны, распространяющиеся и складывающиеся в пространстве.

Найдём результат их сложения. Рассмотрим конкретную точку пространства и найдём в ней результирующий вектор . - по принципу суперпозиции.

Для нас важен квадрат модуля амплитуды суммарной волны, т.к. данная величина пропорциональна вектору Поинтинга.

.

Назовём квадрат модуля амплитуды плоской волны её интенсивностью. Тогда:

Т.е. результирующая интенсивность другая.

Сложение волн при котором суммарная интенсивность не равна сумме интенсивностей волн – явление интерференции.

Об интерференции мы говорим в том случае, когда интенсивность от суммы двух волн не равна сумме их интенсивностей.

Пусть распространяются две электромагнитные волны и , и пусть эти волны приходят в рассматриваемую точку 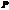с сонаправленными, или противоположно направленными векторами. Посмотрим, как будет выглядеть интерференция.

Пусть

, .

Введем комплексную амплитуду , .

.

Если умножим на комплексно – сопряженную амплитуду, то получим величину пропорциональную вектору Пойнтинга . , где , .

.

Усредним полученную интенсивность по времени:

Если интеграл равен нулю, то - никакой интерференции нет.

Рассмотрим несколько случаев

1) , ,

- возникает интерференция.

2) величина случайным образом зависит от времени. В этом случае среднее значение косинуса равно нулю - интерференции нет.

3) величина случайна, но распределена не равномерно, тогда - возникает интерференция.

Важно заметить, что мы рассматривали не каждую фазу в отдельности, а их разность .

Если при некотором значении разности фаз интеграл , то волны называются абсолютно когерентные.

За счет перемещения точки наблюдения можно добиться любого значения величины , т.к. , .

Если волны абсолютно когерентные, то это значит, что разность их фаз всегда равна нулю, т.е. атомы «выплевывают» синусоиды одновременно и одинаковой длины.

Если при некотором значении разности фаз интеграл , то волны называются абсолютно некогерентные.