Мощность в цепях переменного тока.

Рассмотрим конденсатор. Напряжение на конденсаторе в случае переменного тока можно записать 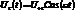. Внутри конденсатора существует электрическое поле 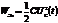. Усредним значение электрического поля по времени. .

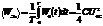Мгновенная мощность выделяемой на конденсаторе энергии есть скорость приращения энергии электрического поля .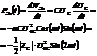

Мгновенная мощность, выделяемая на конденсаторе, меняет свой знак. Если синус больше нуля, энергия конденсатора убывает – часть запасенной энергии конденсатор отдает остальной цепи и частично генератору. Если синус меньше нуля, энергия конденсатора возрастает. Заметим, что средняя мощность, выделенная на конденсаторе равна нулю 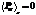! Аналогично можно рассмотреть превращение магнитного поля катушки , .

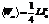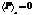Рассмотрим омическое сопротивление. Независимо от направления движения тока в цепи происходит выделение Джоулева тепла. В этом случае, энергия, которую поставляет генератор теряется бесполезно. 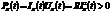. Пусть 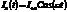, тогда

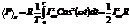
Если рассмотреть любую сложную цепь, то полная мощность, развиваемая генератором равна сумме мощностей выделенных на отдельных элементах цепи.

Мгновенная мощность, выделяемая на генераторе равна произведению тока и напряжения на генераторе. Пусть ток и напряжение на генераторе зависят от времени следующим образом 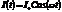, , 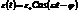тогда

Проведем усреднение по периоду .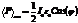

Опять рассмотрим следующую схему

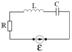Докажем, что средняя за период мощность, выделяемая на генераторе равна Джоулевому теплу.

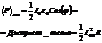
Импеданс нашей цепи 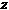имеет вид 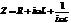, значит 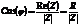. Учтем, что .

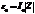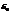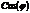Теперь подставим и в выражение для средней мощности генератора. .

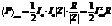Иногда вводят понятие активной и реактивной мощности.

Примем начальную фазу тока через генератор равной нулю.

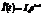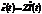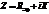, , , где 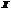- реактивное сопротивление (сумма индуктивного и емкостного сопротивления).

Попытаемся определить мощность.

Мощность – произведение тока и напряжения - произведение двух комплексных чисел. При умножении комплексных чисел их реальные и мнимые части перепутываются. Но первый и второй законы Кирхгофа - операции сложения. Чтобы реальные токи можно было заменять комплексными, и их мнимые и действительные части не перепутывались, при определении мощности мы должны выделить действующие части тока и напряжения.

Пусть 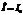, тогда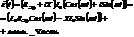

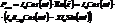
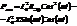
Слагаемое 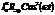называется активной мощностью и измеряется в (Вт). Слагаемое 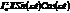называется реактивной мощностью и измеряется в (ВАР).

Средняя за период мощность, выделяемая на генераторе равна активной мощности 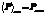. Средняя за период реактивная мощность равна нулю.

Колебания систем с двумя степенями свободы.

Связанные маятники.

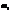1) Рассмотрим систему, состоящую из двух математических маятников, которые связаны идеальной, невесомой пружиной. Длина нити обоих маятников , массы и 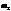соответственно, жесткость пружины .

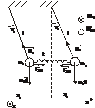
Каждый маятник совершает движение по окружности, поэтому запишем уравнение моментов.

.

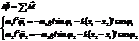Колебания малы, тогда:

.

.

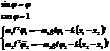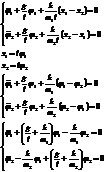Переобозначив коэффициенты при углах, получим:

.

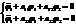Таким образом, колебания связанных маятников описываются системой дифференциальных уравнений второго порядка с постоянными коэффициентами.

2) Рассмотрим два индуктивно связанных колебательных контура (аналог связанных маятников).

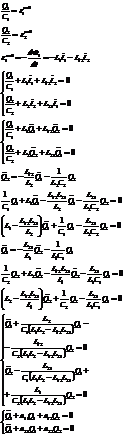
Получили аналогичную систему уравнений.

.

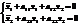Решение данной системы будем искать в виде:

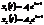
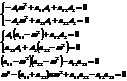
Биквадратное уравнение. В общем случае есть четыре решения. Физически реальных решений будет два: 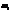и .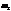

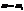
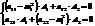
Решений бесконечно много.

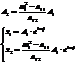
Одно из решений системы. Их бесконечно много с точностью до .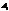

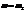
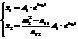
Запишем общее решение уравнений.

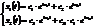
Движение маятника представляет собой суперпозицию двух гармонических колебаний с разными частотами. Следовательно, колебания негармонические.

Пусть маятники будут одинаковыми

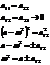
Пусть мало, тогда

.

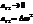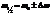
То есть, при слабой связи, складываются колебания с очень близкими частотами, получаются биения.

Волны.

Основные определения. Виды волн. Кинематика волн.

Пусть у нас есть несколько точек, величин, зарядов, которые могут взаимосвязано колебаться. Т.е. если одна точка колеблется то начинают колебаться и остальные.

Например: если есть много маятников последовательно связанных пружинами то постепенно начнут колебаться все маятники, и при том неодинаково.

Пример: камень, брошенный в воду. Т.к. вода обладает конечной вязкостью, т.е. трением, образуются подъёмы и спады уровня воды – колебания.

В волнах никакого переноса массы в воде не бывает, вода не движется от камня, она движется вверх и вниз.

Опр.: Волной называется распространение в среде колебательного движения.

Обозначим колеблющуюся величину, изменяющуюся во времени, как .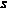

Данная величина может быть двух видов:

- Скаляр: плотность воздуха в окрестности некоторой точки (например при разговоре), заряд и т.д. Т.е. .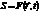

- Вектор: радиус вектор некоторой частицы, напряжённость электрического поля, индукция и т.д. Т.е. 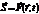или .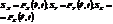

В подобной записи можно описать любой процесс. Если функция - синус или косинус, то такие волны называются гармоническим или синусоидальными.

Будем считать, что аргумент имеет вид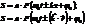

или

.

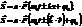Если волны можно записать в подобной форме, то волны называются линейными.

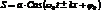и т.д. и т.п. – это линейные гармонические волны.