Шпаргалка по физике за 4 семестр

Шпаргалка по физике за 4 семестр

Гармонические колебания.

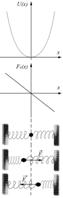
Рассмотрим движение частицы в некотором однородном поле. Будем задавать его (поле) не силами, а потенциальной энергией (т.е. силы консервативны). Пусть диссипативных сил нет. Рассмотрим следующий вид зависимости потенциальной энергии от координаты.

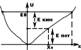
Пусть минимум потенциальной энергии в точке (0,0). Такое поле – потенциальная яма.

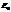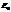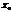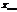Пусть в некоторый момент времени, когда точка была в нуле, телу сообщили кинетическую энергию , т.к. нет диссипативных сил, то полная механическая энергия постоянна и равна . В точке , частица имеет потенциальную энергию, определяющейся точкой на графике. При движении по оси будет расти потенциальная энергия и уменьшаться кинетическая, и в некоторой точке потенциальная энергия станет равна 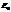а кинетическая станет равна нулю.

Частица совершает непрерывные движения в ограниченной области пространства повторяя свою траекторию – это колебательное движение.

Пусть колебания малые. Разложим 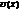в ряд Тейлора вблизи ноля:

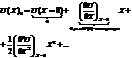
Допустим, что колебания настолько малы, что мы с достаточной погрешностью можем ограничиться квадратичным слагаемым. Тогда:

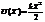, где .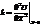

Т.о. если энергия мала, то низ ямы можно представить как параболу.

; ;

; .

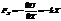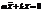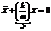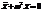Мы рассмотрели как описывать механические движения в потенциальной яме. Если колебания на столько маленькие, что «дно ямы» можно описать параболой, то колебания описываются формулой 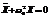, аналогично могут описываться и большие колебания, при условии, что яма параболическая.

Рассмотрим параболическую яму или самое донышко любой другой.

Итак, зависимость потенциальной энергии тела от координаты имеет вид 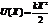. Найдем зависимость силы, действующей на тело, от его координаты: 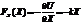. Заметим, что эта сила линейна.

Решим дифференциальное уравнение 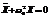, описывающее движение в параболической яме.

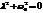
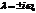
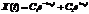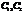, - в общем случае произвольные комплексные числа. Поскольку 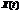- действительная величина, то всегда выполняется соотношение 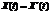, а значит 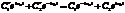это тождество верно для любого момента времени .

Если , .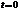

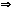
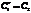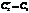
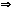
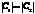Пусть 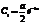, , 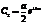где 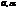- некоторые произвольные действительные числа.

Запишем решения в другом виде .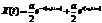

Запишем комплексные числа в тригонометрическом виде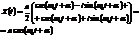

распишем косинус суммы ,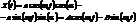

где , .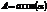

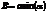Все, что колеблется по такому закону называется «гармонические колебания»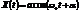

Величина называется амплитудой гармонических колебаний,

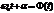- фаза гармонических колебаний – величина, зависящая от времени. - начальная фаза.

Если координата записывается 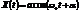, то скорость и ускорение записываются соответственно , .

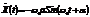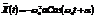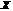Найдем такое время , через которое повторится, т.е. выполняется равенство 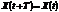. 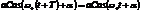, , 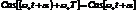, 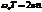где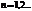

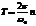величина называется периодом колебаний. Периодов много, но можно рассматривать наименьший .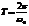

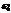- круговая (циклическая) частота колебаний .

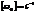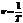- называется «просто» частота колебаний. .

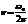Энергия колебаний.

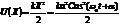
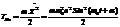
Энергия осциллирует и всегда положительна.

.

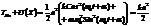Полная энергия не зависит от времени – сохраняется. 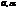- произвольные постоянные в общем решении дифференциального уравнения, их можно найти из начальных условий.

Н.р. ,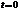

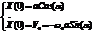решив эту систему, найдем 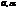, зная 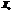и , , .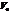

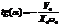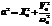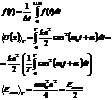
Сложение колебаний

Представим, что шарик движется в двух полях, н.р. заряженный математический маятник рядом с которым симметрично расположены заряды одинакового знака. Шарик движется финитно. В этом случае шарик не обязательно будет совершать гармонические колебания, даже если обе ямы параболические. Процесс нахождения результирующего колебания называется сложение колебаний. Суммарное колебание зависит от характера колебаний. До этого мы рассматривали колебания скалярной величины, но может колебаться и вектор, а скаляр – это его проекция. Суммарное колебание зависит от - одинаковая она или разная.

Пусть отдельно уравнения колебаний для гравитационного и кулоновского поля имеют вид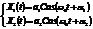

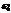- одинаковые, но разные начальные фазы колебаний.

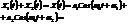
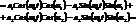
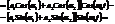
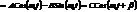
Итак, сумма двух гармонических колебаний с одинаковой частотой 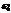есть гармонические колебания.

Посмотрим, как складываются гармонические колебания с разными частотами.

Разберем частный случа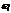й: и 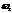чуть-чуть отличаются друг от друга. Пусть амплитуды и начальные фазы колебаний одинаковы.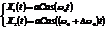

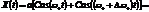
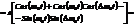
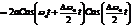
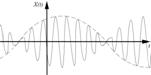
при .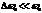

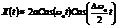Точная настройка двух струн на гитаре означает, что мы стремим 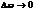, , 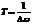т.е. .

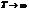Если гитара расстроена, то 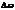- значительно, и две струны, расположенные рядом, издают звук похожий на «ау-ау» с периодом .

Результат сложения двух близких по частоте колебаний называется биение. Если частоты хотя бы немного различаются, то колебания становятся не гармоническими (биения).

Затухающие колебания.

Пусть есть трение. В общем случае трение пропорционально скорости. Запишем второй закон Ньютона.

.

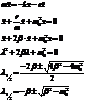1)

.

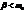
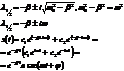Получили негармонические колебания с меньшей частотой.

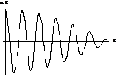
Такие колебания называются затухающими колебаниями.

Найдем время, за которое амплитуда колебаний уменьшиться в раз.

.

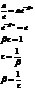– характерное время затухания.

Во сколько раз измениться амплитуда за период?

.

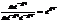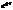– декремент затухания.

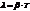– логарифмический декремент затухания.

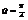– добротность системы.

Пусть есть диссипативные силы (силы трения) в общем случае пропорциональные скорости.

;

;

.

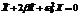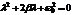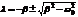1) 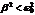- рассмотрено раньше.

2) .

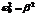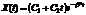- т.е. функция.

Рассмотрим два вида начальных условий:

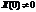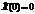- ; (т.е. шарик на нитке или пружине только оттянули). Тогда .

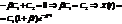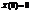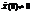- ; (т.е. шарику сообщили некоторую скорость). Тогда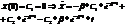

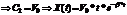
Т.е. шарик отклонится и вернётся обратно.

3)

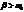
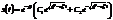
Вынужденные колебания.

Добавим вынуждающую силу, действующую на осциллятор.

;

;

.

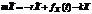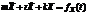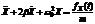Пусть 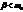. Рассмотрим случай, когда 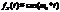. Тогда

.

.

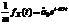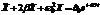Тогда частное решение этого дифференциального уравнения выглядит так:

;

;

;

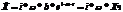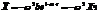откуда: 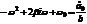. Тогда

.

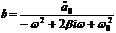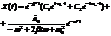, где .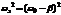

При 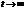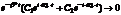, Это случай установившихся колебаний. Если долго ждать, то вид колебаний не будет зависеть от начальных условий

.

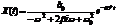Пусть 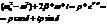, откуда

;

;

.

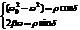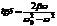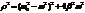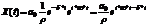возьмём действительную часть:

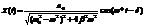Резонанс.

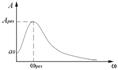
Посмотрим как зависит амплитуда установившихся колебаний от частоты силы.

;

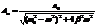Найдём экстремум 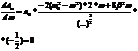. Откуда 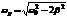- при такой имеет место быть экстремум. Т.к. он единственный 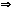что это максимум и амплитуда колебаний будет максимальна. 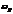определяется 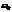- самим осциллятором и вязкостью среды. Ситуация, когда амплитуда вынужденных колебаний достигает максимума – резонанс.

.

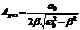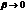
1) 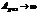, т.е. колебания станут нелинейными.

2) Чем вязкость меньше, тем график амплитуды пойдёт выше.

Найдём такую частоту, при которой 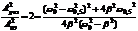. Предположим, что резонансная кривая симметрична и 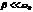, т.е. затухание малое. Тогда

;

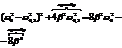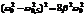, но т.к. кривая узкая т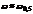о , но

;

;

.

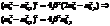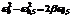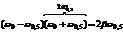Т.о. для систем с малым затуханием выполняется соотношение .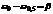

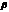- величина, на которую нужно отступить в право или в лево от резонанса, чтобы амплитуда колебаний уменьшилась в два раза.

Величина, 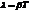называется логарифмический декремент затухания

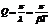- добротность.

Найдем отношение высоты рез­­­­­­онансной кривой к :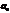

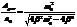
Пусть максимум узкий, тогда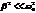

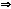
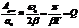
Добротность – это безразмерная величина.

Ее смысл: Если есть вынуждающая сила, то чем больше вязкость, тем меньше максимум. Добротность показывает во сколько раз можно увеличить 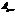по отношению к смещению постоянной силы. Чем больше добротность 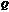,тем больше 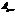, чем меньше добротность 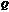, тем меньше .

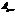Фазовые характеристики резонанса.

Установившиеся колебания 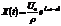повторяют действующую силу 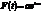не точно, а отстают по фазе на величину .

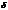Посмотрим, в каком случае .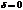

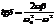- в разных точках кривой начальная фаза колебаний будет разной. 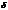зависит от затухания 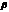и свойства самого осциллятора 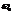. Построим график .

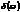Три вспомогательные точки:

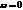
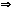
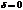
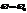
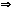
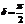
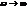
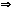
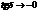
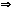
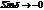
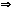
Чем больше частота , тем больше отставание маятника от силы.

При 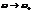отставание стремится к половине периода.

Электрические колебания.

Соберем электрическую цепь.

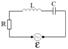
Найдем уравнения, которые описывают заряд на конденсаторе .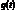

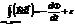будем работать в СИ. Считаем, что ток в данной системе квазистационарный, т.е в заданный момент времени токи во всех точках цепи одинаковые.

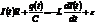(1)

При записи выражения (1) считали, что катушка не деформируется и её индуктивность постоянна, а это значит, что .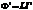

Запишем выражение (1) в другом виде 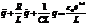и сравним с уже известным уравнением 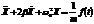. Эти уравнения имеют одинаковый вид. Поэтому, если в формулах, полученных для механических колебаний, заменим константы 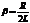и 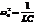, то они будут справедливы для уравнения .

.

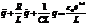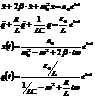Импеданс.

Рассмотрим некоторую разветвлённую цепь содержащую .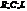

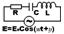
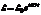- комплексная запись.

Пусть 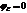, тогда 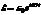. Т.к. токи квазистационарны то для них применимы законы Ома для мгновенных значений переменных величин. Выберем направление обхода по току. Применим закон Ома для Разорванной цепи:

,

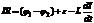где 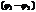- разность потенциалов между положительной и отрицательной обкладками - 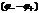. Тогда:

.

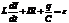Дифференцируя данное выражение по времени, мы получим следующее соотношение:

.

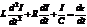Это уравнение вынужденных колебаний, где 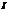- ток в нашей цепи. Если нас интересует установившийся режим колебаний, то в цепи в результате возникают колебания с частотой вынуждающей силы. Тогда, подставим в полученное уравнение следующие выражения:

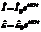
Тогда:

,

.

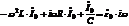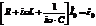Откуда 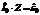, где 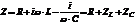- комплексное сопротивление или импеданс.

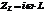- индуктивный импеданс.

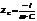- ёмкостной импеданс.

В результате для комплексной амплитуды тока получим следующие выражение:

,

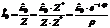где 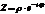, 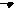- фаза тока по отношению к напряжению. Т.к. 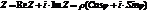, то 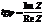(где обе части надо брать с учётом знака).

Метод контурных токов.

Элементарный контур – контур, который нельзя получить наложением других контуров.

Рассмотрим схему:

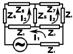
В данной схеме можно выделить три элементарных контура. Будем считать, что по каждому элементарному контуру течёт одинаковый ток. Будем также считать, что все токи текут в одном направлении.

Метод контурных токов позволяет сократить число уравнений на количество узлов.

Составим следующую систему:

.

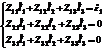Где: 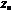- полный импеданс данного контура – сумма импедансов входящих в данный контур ( 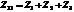); 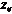- импеданс на соприкасающихся ветвях взятый с обратным знаком ( ).

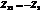Тогда решением этой системы уравнений относительно неизвестных токов будут:

.

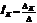Тогда ток через конкретный импеданс будет равен сумме токов в элементарных контурах в которые он входит взятые с учётом выбора направления обхода, т.е.:

, .

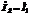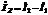Резонанс токов.

Рассмотрим контур.

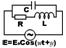
Пусть 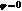. Тогда Имеем для тока текущего через ЭДС:

,

.

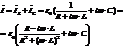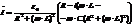Мнимая часть амплитуды тока будет равна нулю при 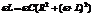. При этом условии данная катушка обладает чисто омическим сопротивлением т.е. и находятся в фазе, т.е. имеет место быть резонанс (так говорят в схемотехнике).

.

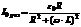При резонансе токов ток через генератор минимален.

В очередной раз рассмотрим следующий контур

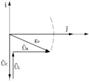
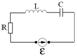
Стрелка указывает направления ЭДС в начальный момент времени.

Изобразим на одном графике зависимости напряжений на сопротивлении, катушке и конденсаторе в зависимости от частоты подаваемого напряжения .

На всех трех графиках возникает максимум при частоте близкой к резонансной .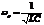

Теперь рассмотрим следующую схему:

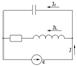
Ранее нами уже было получено выражение для комплексной амплитуды силы тока в цепи .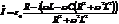

Видим, что при условии 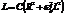данная цепочка будет обладать чисто омическим сопротивлением. Ток и ЭДС находятся в фазе. В этом случае говорят о резонансе токов. В случае 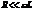эту резонансную частоту можно приближенно считать равной 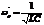. Но истинная резонансная частота зависит от добротности 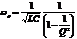, где 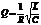. Найдем значения токов в ветвях контура при резонансной частоте. .

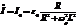Рассмотрим случай 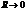, тогда 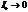. Полный ток в цепи равен нулю. При этом ток в цепи с конденсатором не нулевой. 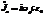и опережает ЭДС по фазе на 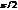. Ток в ветви с катушкой 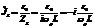отстает от ЭДС на 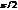. Токи через катушку и конденсатор совпадают по амплитуде, но противоположно направлены.

В идеальном контуре токи в ветвях с конденсатором и индуктивностью достигают достаточно больших значений и протекают в противоположных направлениях. Начальная энергия, которой обладает колебательный контур при резонансе, была получена сразу после замыкания ключа в процессе установления.

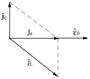
Проиллюстрируем на векторных диаграммах случаи резонанса напряжений.

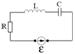Подаваемое на цепочку напряжение равно сумме напряжений на конденсаторе, сопротивлении и индуктивности 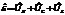. Каждой из этих комплексных величин ставится в соответствие вектор на комплексной плоскости 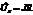, , 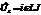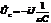. Цепь не разветвленная, значит, во всех элементах цепи течет одинаковый ток.

Пусть начальная фаза тока равна нулю и 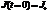. Если величина достаточно мала, то величина 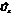тоже мала. При увеличении вектор 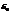будет разворачиваться, и при совпадении с направлением 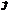наступит резонанс.

Построим векторную диаграмму токов при нулевом сопротивлении. За нуль возьмем фазу ЭДС 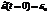. Учтем, что по первому правилу Кирхгофа, сумма токов равна нулю .

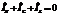При резонансе .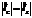

Если сопротивление не равно нулю, то получим следующую диаграмму токов.

Связанные маятники.

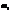1) Рассмотрим систему, состоящую из двух математических маятников, которые связаны идеальной, невесомой пружиной. Длина нити обоих маятников , массы и 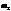соответственно, жесткость пружины .

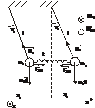
Каждый маятник совершает движение по окружности, поэтому запишем уравнение моментов.

.

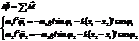Колебания малы, тогда:

.

.

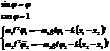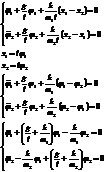Переобозначив коэффициенты при углах, получим:

.

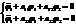Таким образом, колебания связанных маятников описываются системой дифференциальных уравнений второго порядка с постоянными коэффициентами.

2) Рассмотрим два индуктивно связанных колебательных контура (аналог связанных маятников).

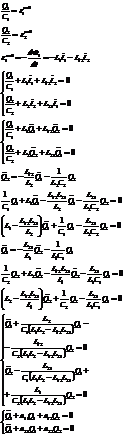
Получили аналогичную систему уравнений.

.

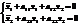Решение данной системы будем искать в виде:

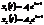
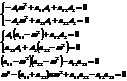
Биквадратное уравнение. В общем случае есть четыре решения. Физически реальных решений будет два: 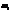и .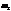

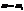
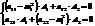
Решений бесконечно много.

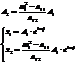
Одно из решений системы. Их бесконечно много с точностью до .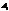

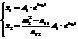
Запишем общее решение уравнений.

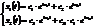
Движение маятника представляет собой суперпозицию двух гармонических колебаний с разными частотами. Следовательно, колебания негармонические.

Пусть маятники будут одинаковыми

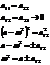
Пусть мало, тогда

.

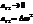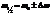
То есть, при слабой связи, складываются колебания с очень близкими частотами, получаются биения.

Волны.

Основные определения. Виды волн. Кинематика волн.

Пусть у нас есть несколько точек, величин, зарядов, которые могут взаимосвязано колебаться. Т.е. если одна точка колеблется то начинают колебаться и остальные.

Например: если есть много маятников последовательно связанных пружинами то постепенно начнут колебаться все маятники, и при том неодинаково.

Пример: камень, брошенный в воду. Т.к. вода обладает конечной вязкостью, т.е. трением, образуются подъёмы и спады уровня воды – колебания.

В волнах никакого переноса массы в воде не бывает, вода не движется от камня, она движется вверх и вниз.

Опр.: Волной называется распространение в среде колебательного движения.

Обозначим колеблющуюся величину, изменяющуюся во времени, как .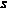

Данная величина может быть двух видов:

- Скаляр: плотность воздуха в окрестности некоторой точки (например при разговоре), заряд и т.д. Т.е. .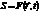

- Вектор: радиус вектор некоторой частицы, напряжённость электрического поля, индукция и т.д. Т.е. 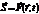или .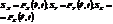

В подобной записи можно описать любой процесс. Если функция - синус или косинус, то такие волны называются гармоническим или синусоидальными.

Будем считать, что аргумент имеет вид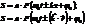

или

.

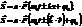Если волны можно записать в подобной форме, то волны называются линейными.

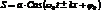и т.д. и т.п. – это линейные гармонические волны.

Волновое уравнение.

Волновое уравнение вывести нельзя – оно фундаментально, это из него все получаются уравнения различных волн.

Попробуем угадать вид волнового уравнения. Для этого запишем уравнение плоской волны 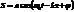и продифференцируем его дважды по времени и координате.

, ,

, .

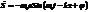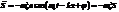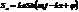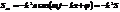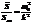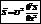Из этих уравнений видно, что или , где 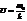- фазовая скорость.

Обобщим и в другом виде запишем 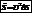, где 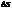- оператор Лапласа от S.

Докажем, что любая функция вида 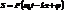является решением уравнения .

, ,

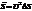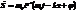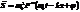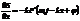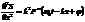, теперь сразу видно, что 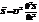для любой функции вида .

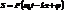Плотность потока энергии.

Рассмотрим продольную волну в твердом теле.

Равновесные характеристики: .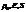

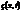– смещение.

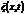– скорость смещения.

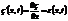– относительная деформация.

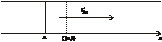
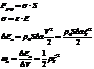
- плотность кинетической энергии.

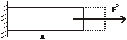
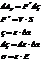
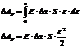
Растянутый стержень обладает упругой энергией:

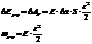
- плотность энергии, локализованной в данном элементе:

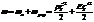
Энергия может переноситься.

Найдем выражение для плотности потока энергии.

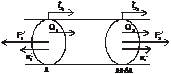
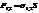
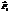За время силы и 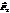совершают работу.

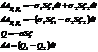
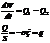
– плотность потока энергии.

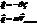
– вектор Умова.

Стоячие волны.

Принцип суперпозиции: Если одно и тоже вещество колеблется одновременно по двум различным законам, то в итоге суммарное колебание будет равно сумме различных колебаний.

Пусть распространяются две волны в одной и той же среде:

.

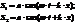Т.е. у них одинаковы модули но противоположны направления волновых скоростей. По принципу суперпозиции:

.

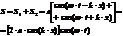Построим изображение данной волны в некоторые моменты времени (сфотографируем волну).

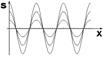
Попробуем найти такие , что