Условие параллельности двух плоскостей.

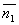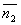Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

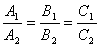Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

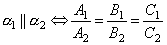или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .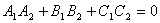

Таким образом, .

Прямая в пространстве и ее различные уравнения. Угол между прямыми и между прямой и плоскостью. Точка пересечения прямой и плоскости.

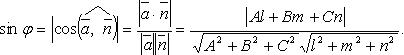
угол между прямой и плоскостью

19. Геометрические объекты в пространстве Rⁿ (прямая, луч, отрезок, гиперплоскость)

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

Итак, если уравнения двух непараллельных плоскосте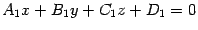й

и

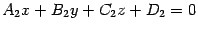, то прямая, являющаяся их линией пересечения, задается системой уравнений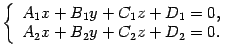

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.

Скалярное произведение в н-мерном пространстве. Определение, свойства, угол между векторами.

Эллипс. Вывод канонического уравнения.

Эллипс.

Эллипсомназывается множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F₁ и F₂ эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему

у М(х,у) координат так, чтобы ось Ох совпала с прямой F₁F₂, начало

r₁ r₂ координат – с серединой отрезка F₁F₂. Пусть длина этого

отрезка равна 2с, тогда в выбранной системе координат

F₁ O F₂ x F₁(-c, 0), F₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и

сумма расстояний от нее до F₁ и F₂ равна 2а.

Тогда r₁ + r₂ = 2a, но ,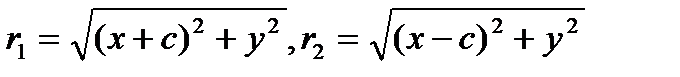

поэтому 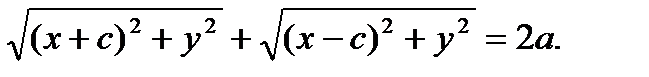Введя обозначение b² = a²-c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: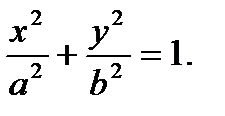

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника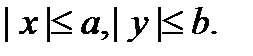

3) Эксцентриситет эллипса e < 1.

Можно доказать, что уравнение (11.7) равносильно исходному уравнению.

Оно называется каноническим уравнением эллипса. Эллипс- кривая второго порядка.