Определим значения переменных, входящих в область допустимых значений.

Очевидно, что 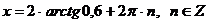входят в область допустимых значений и являются корнями уравнения.

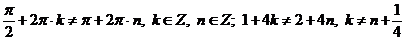- это неравенство выполняется при любых целых значениях n и k, значит 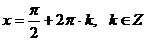являются решениями уравнения.

Ответ: .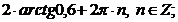

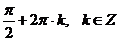Пример 148. Решите уравнение .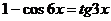

Решение

Область допустимых значений: .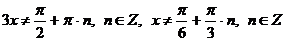

Выразим , получим уравнение:

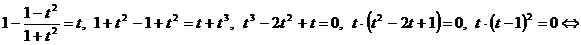
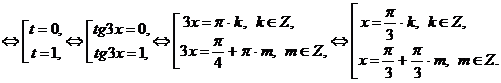
Выясним, входят ли эти значения переменной в область допустимых значений:

.

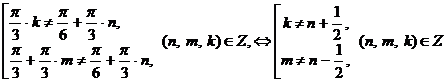Оба неравенства выполняются при любых целых значениях n, m и k, значит, оба множества корней входят в область допустимых значений.

Ответ: .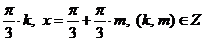

Пример 149. Решите уравнение .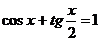

Решение

Область допустимых значений .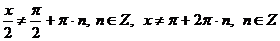

Выразим 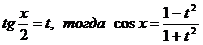, получим уравнение:

.

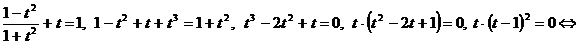
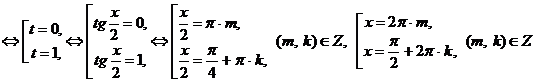Выясним, входят ли эти значения переменной в область допустимых значений:

.

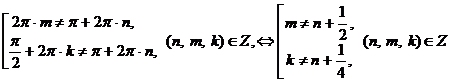Оба неравенства выполняются при любых целых значениях n, m и k, значит, оба множества корней входят в область допустимых значений.

Ответ: .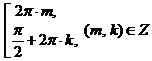

Пример 150. Решите уравнение .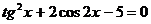

Решение

Область допустимых значений: .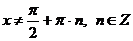

Выразим 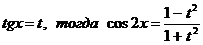, получим уравнение:

.

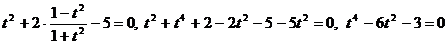Это биквадратное уравнение: ,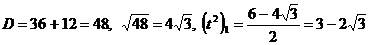

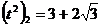. Уравнение 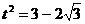не имеет решений, так как правая часть отрицательна.

.

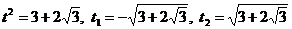Получим совокупность уравнений:

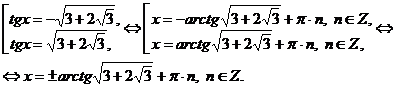
Эти корни входят в область допустимых значений.

Ответ: .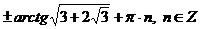

Пример 151. Решите уравнение .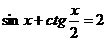

Решение

Область допустимых значений: .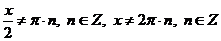

Выразим 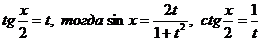, , 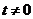получим уравнение:

.

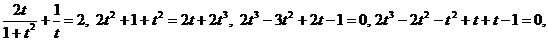
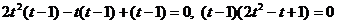Это уравнение равносильно совокупности уравнений: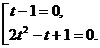

Второе уравнение не имеет корней, так как его дискриминант отрицателен.

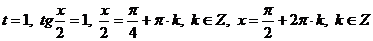
Эти корни входят в область допустимых значений.

Ответ: .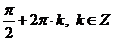

Пример 152. Решите уравнение .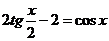

Решение

Область допустимых значений переменной: .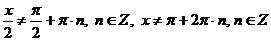

Выразим 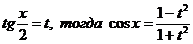, получим уравнение:

.

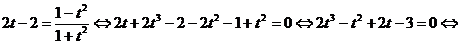
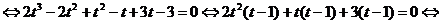
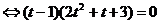Полученное уравнение равносильно совокупности уравнений:

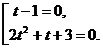Второе уравнение совокупности имеет отрицательный дискриминант и не имеет действительных корней. Получаем один корень: t = 1.

.

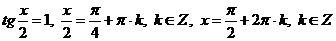Выясним, входят ли эти значения переменной в область допустимых значений:

.

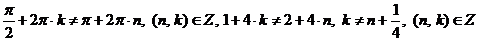Как видим, последнее неравенство выполняется при любых целых значениях n и k, а, значит, корни входят в область допустимых значений.

Ответ: .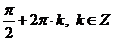

Пример 153. Решите уравнение .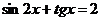

Решение

Область допустимых значений: .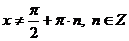

Пусть 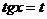, тогда 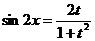, получим уравнение:

.

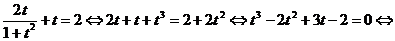
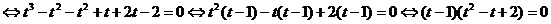Полученное уравнение равносильно совокупности уравнений:

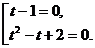Второе, квадратное уравнение этой совокупности имеет отрицательный дискриминант и не имеет действительных корней. Находим: t = 1.

.

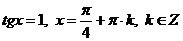Выясним, входят ли эти значения переменной в область допустимых значений:

.

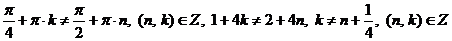Как видим, последнее неравенство выполняется при любых целых значениях n и k, а, значит, 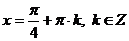входят в область допустимых значений и являются корнями уравнения.

Ответ: .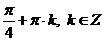

Пример 154. Решите уравнение .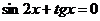

Решение

Область допустимых значений: .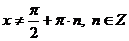

Пусть 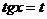, тогда 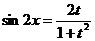, получим уравнение:

.

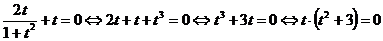Полученное уравнение равносильно совокупности уравнений: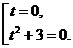

Второе, квадратное, уравнение этой совокупности не имеет действительных корней, тогда, получим: .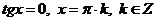

Выясним, входят ли эти значения переменной в область допустимых значений:

.

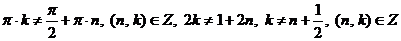Как видим, последнее неравенство выполняется при любых целых значениях n и k, а, значит, 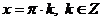входят в область допустимых значений и являются корнями уравнения.

Ответ: .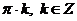

Пример 155. Решите уравнение .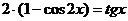

Решение

Область допустимых значений: .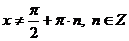

Пусть 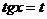, тогда 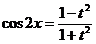, получим уравнение:

.

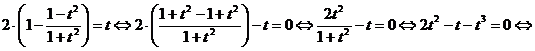
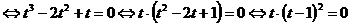Полученное уравнение равносильно совокупности уравнений:

.
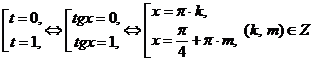