Определим, входят ли эти значения в область допустимых значений.
Проверим значения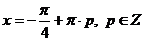 
.
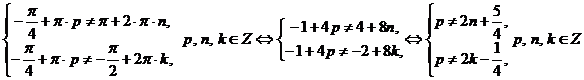
Оба неравенства выполняются при всех 
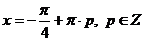, значит - решения уравнения.
Проверим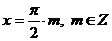 
.
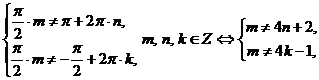значит, m может принимать значения равные: m = 4n и m = 4n + 1, отсюда находим 
.
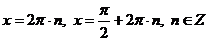Ответ: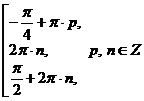 
.
Пример 121. Решите уравнение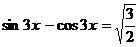 
.
Решение
(Это один из способов решения. Другие будут приведены ниже).
Положим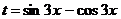 
, тогда 
, 
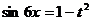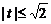, получим систему уравнений:
.
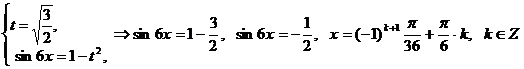Ответ: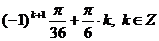 
.
Задание 5
122. 
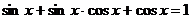. 123. 
.
124. 
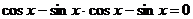. 125. 
.
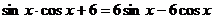126. 
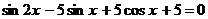. 127. 
.
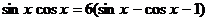4.2. Замена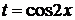 
При такой замене через t легко выражаются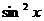 
и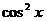 
:
.
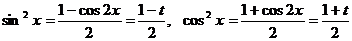Если левая часть тригонометрического уравнения выражается через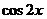 
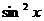, и 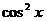, то можно выполнить замену переменных по формулам
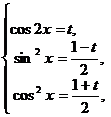причем 
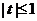. (1)
Рассмотрим, например, уравнение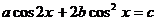 
.
Это уравнение можно привести к однородному уже известным нам способом.
Однако проще его решить с помощью замены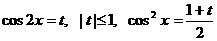 
, получим уравнение: 
.
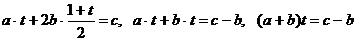Делая обратную подстановку, получим уравнение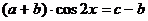 
.
(К такому же результату можно придти заменив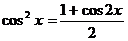 
).
Аналогично можно решать уравнения вида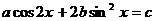 
.
(В этом уравнении замена основана на формуле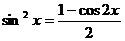 
).
Пример 128. Решите уравнение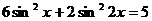 
.
Решение
Преобразуем уравнение:
.
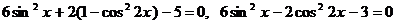Выполним замену: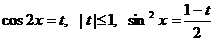 
, получим уравнение:
.
.
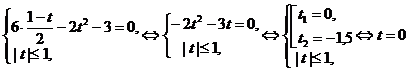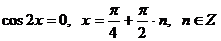Ответ: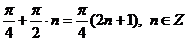 
.
Пример 129. Решите уравнение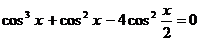 
.
Решение
Преобразуем уравнение, используя формулы: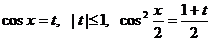 
, получим уравнение: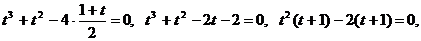 
.
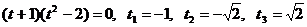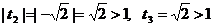- эти корни не удовлетворяют условию 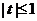и являются посторонними, 
.
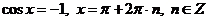Ответ: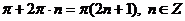 
.
Пример 130. Решите уравнение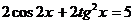 
.
Решение
Область допустимых значений: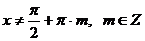 
.
Выполним замену: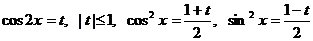 
, получим:
.
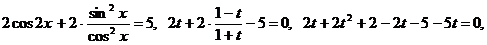
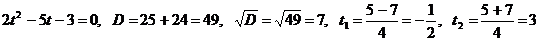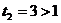- не удовлетворяет условию 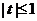и является посторонним корнем.
.
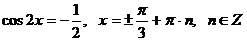Определим значения x, которые входят в область допустимых значений.
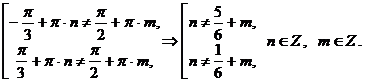
Совокупность неравенств, каждое из которых выполняется при всех любых целых значениях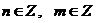 
, показывает, что все значения x входят в область допустимых значений.
Ответ: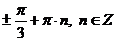 
.
Пример 131. Решите уравнение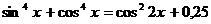 
.
Решение
Выполним замену: 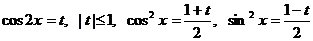, получим:
.
.
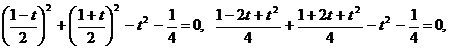
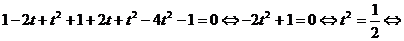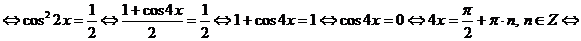
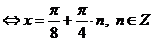Ответ: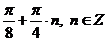 
.
4.3. Случаи, когда в уравнении не содержится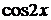 
Пример 132. Решите уравнение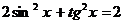 
.
Решение
Область допустимых значений: .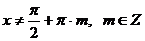
Выполним замену: 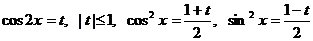, получим:
;
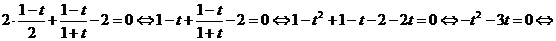
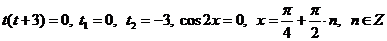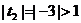- не удовлетворяет условию 
.
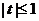Определим значения x, которые входят в область допустимых значений.
Сразу ясно, что вторая группа корней не входит в область допустимых значений. Проверим первую группу корней:
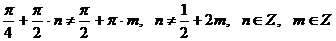- это значит, что все значения из множества 
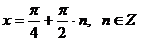входят в область допустимых значений.
Ответ: .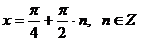
Пример 133. Решите уравнение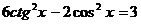 
.
Решение
Область допустимых значений: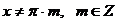 
.
Выразим: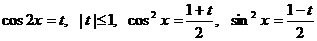 
, получим:
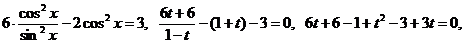
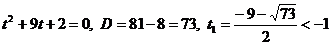- не удовлетворяет условию 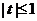и является посторонним корнем.
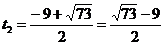- удовлетворяет уравнению.
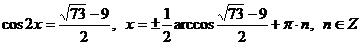- эти значения входят в область допустимых значений.
Ответ: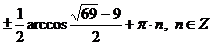 
.
Пример 134. Решите уравнение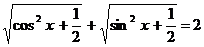 
.
Решение
Выразим: 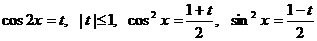, получим:
.
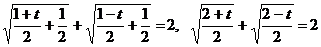Возведем обе части уравнения в квадрат, получим:
.
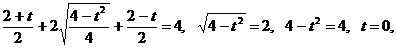
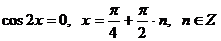Ответ: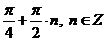 
.
Пример 135. Решите уравнение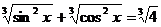 
.
Решение
Выразим: 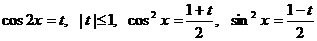, получим:
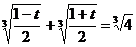. Возведем обе части уравнения в куб, получим:
.
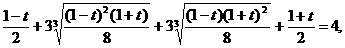
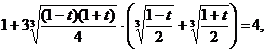
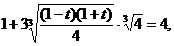
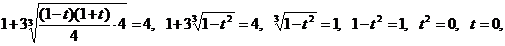
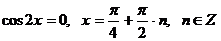Ответ: 
.