Материал подготовлен учителем математики Тишиным Владимиром Ивановичем.
Тишин В. И.
Основные методы
решения
тригонометрических
Уравнений
Г.
Материал подготовлен учителем математики Тишиным Владимиром Ивановичем.
Года
Содержание
Тригонометрические уравнения. 4
1. Метод разложения на множители. 4
Задание 1. 18
2. Метод замены переменных и сведение к алгебраическим уравнениям 18
2.1. Применение формул двойного и половинного аргумента. 21
2.2. Применение формул приведения. 26
Задание 2. 30
3. Уравнения, однородные относительно  и
и  ....... 31
....... 31
3.1. Применение формул приведения. 34
Задание 3. 37
Задание 4. 40
4. Метод замены переменных. 41
4.1. Замена 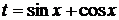 . 41
. 41
Задание 5. 45
4.2. Замена 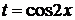 ............ 45
............ 45
4.3. Случаи, когда в уравнении не содержится 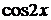 ........ 47
........ 47
4.4. Случаи, когда аргументы кратны 2x и x. 49
Задание 6. 51
4.5. Замена  . Универсальная тригонометрическая подстановка 51
. Универсальная тригонометрическая подстановка 51
Задание 7. 58
5. Метод оценки левой и правой частей уравнения. 59
Задание 8. 63
6. Введение вспомогательного аргумента. 64
Задание 9. 67
7. Системы тригонометрических уравнений. 68
Задание 10. 70
Задание 11. 72
Ответы.. 73
К заданию 1. 73
К заданию 2. 73
К заданию 3. 73
К заданию 5. 73
К заданию 6. 74
К заданию 7. 74
К заданию 9. 74
Тригонометрические уравнения
Метод разложения на множители
Пример 1. Решите уравнение 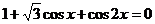 .
.
Решение
Преобразуем уравнение. Применим формулу:
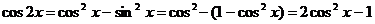 .
.
Получим уравнение: 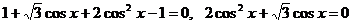 .
.
Это уравнение решим разложением на множители: 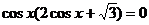 .
.
Получим совокупность уравнений:
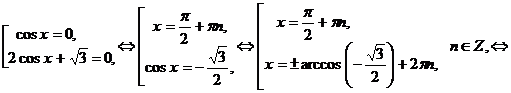
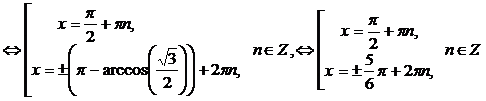 .
.
Ответ: 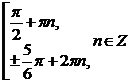 .
.
Пример 2. Решите уравнение 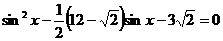
Решение
Преобразуем уравнение: 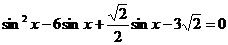
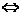
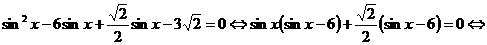
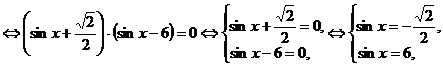
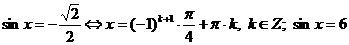 - решений не имеет.
- решений не имеет.
Ответ: 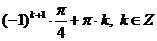 .
.
Пример 3. Решите уравнение 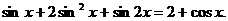
Решение
Преобразуем уравнение. Применим формулы:
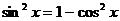 и
и 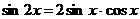 .
.
Получим уравнение: 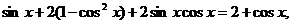
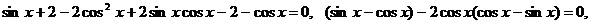
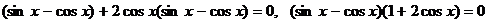 .
.
Получим совокупность двух уравнений:
(1) 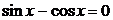 и (2)
и (2) 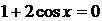 .
.
Уравнение (1) 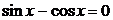 является однородным. В нем
является однородным. В нем 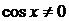 . В самом деле, если допустить противное, т. е., что
. В самом деле, если допустить противное, т. е., что 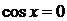 , тогда, подставив его в уравнение (1), найдем, что и
, тогда, подставив его в уравнение (1), найдем, что и 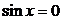 , что невозможно при одних и тех же значениях аргумента (в частности, не будет выполняться основное тригонометрическое тождество
, что невозможно при одних и тех же значениях аргумента (в частности, не будет выполняться основное тригонометрическое тождество 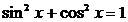 ). Итак,
). Итак, 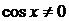 .
.
Разделим обе части уравнения (1) на 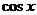 , получим
, получим 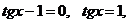
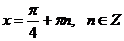 .
.
Решим второе уравнение: 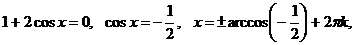
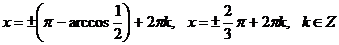 .
.
Ответ: 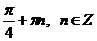 ,
, 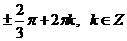 .
.
Пример 4. Решите уравнение 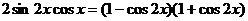 .
.
Решение
Преобразуем уравнение.
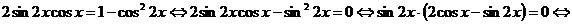
Уравнение примет вид:
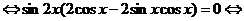
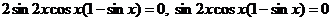 .
.
Полученное уравнение равносильно совокупности уравнений:
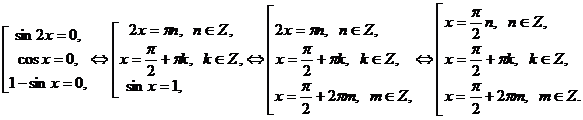
Объединим полученные решения, если это возможно. Попробуем выработать общие принципы для объединения нескольких решений в одно.
Объединим два последних решения в одно: 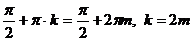 - это значит, что при четных значениях k из множества корней
- это значит, что при четных значениях k из множества корней 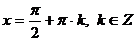 получаются корни
получаются корни 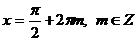 , значит,
, значит, 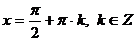 являются общими решениями двух последних решений.
являются общими решениями двух последних решений.
Далее, найдем общие решения 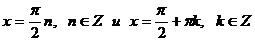 .
.
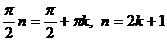 , т. е. при нечетных значениях n из первого множества корней
, т. е. при нечетных значениях n из первого множества корней 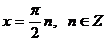 получаются корни
получаются корни 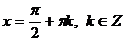 , следовательно,
, следовательно, 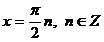 - являются общими решениями трех полученных результатов.
- являются общими решениями трех полученных результатов.
Ответ: 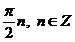 .
.
Пример 5. Решите уравнение 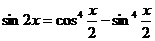 .
.
Решение
Преобразуем уравнение 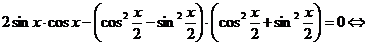
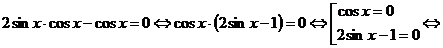
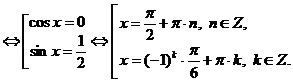
Ответ: 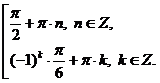
Пример 6. Решите уравнение 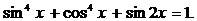
Решение
Преобразуем уравнение, для этого прибавим к левой части уравнения и вычтем, чтобы выражение не изменилось, произведение 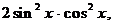 тогда уравнение примет вид
тогда уравнение примет вид
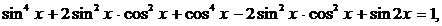
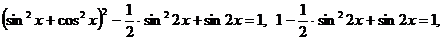
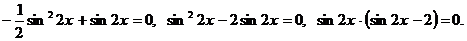
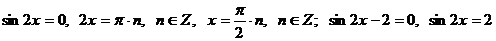 - это уравнение не имеет решений, так как
- это уравнение не имеет решений, так как 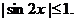
Ответ: 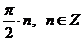 .
.
Пример 7. Решите уравнение 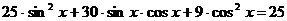 .
.
Решение
I-й способ
Левая часть этого уравнения представляет собой однородное выражение относительно 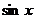 и
и 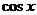 . Уравнение было бы однородным, если бы в правой части уравнения был нуль.
. Уравнение было бы однородным, если бы в правой части уравнения был нуль.
Для преобразования уравнения в однородное, правую часть представим в виде: 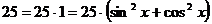 .
.
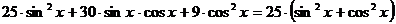 , а затем все перенесем в левую часть и приведем подобные слагаемые:
, а затем все перенесем в левую часть и приведем подобные слагаемые:

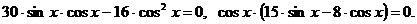
II-й способ
Преобразуем уравнение. Перенесем 25 из правой части в левую и сгруппируем с первым членом, получим: 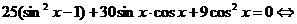

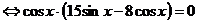 .
.
Полученное уравнение равносильно совокупности двух уравнений:
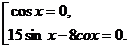
Решая первое уравнение, находим: 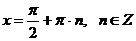 .
.
Второе уравнение является однородным первой степени, 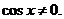
Если допустить, что 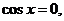 тогда подставив это значение в уравнение, получаем:
тогда подставив это значение в уравнение, получаем: 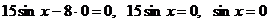 . Но одновременно
. Но одновременно 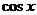 и
и 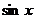 не могут равняться нулю. Итак,
не могут равняться нулю. Итак, 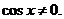 Разделим на него обе части уравнения, получим:
Разделим на него обе части уравнения, получим:
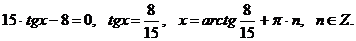
Ответ: 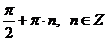 ,
, 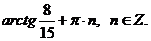
Пример 8. Решите уравнение 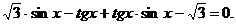
Решение
Область допустимых значений переменной: 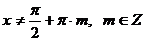 .
.
Преобразуем уравнение:
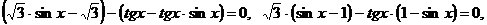
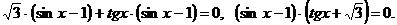
Это уравнение равносильно совокупности двух уравнений:
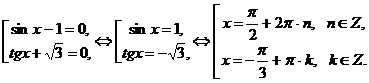
Решение
Преобразуем разность синусов  в произведение, получим
в произведение, получим

С учетом этого преобразования, уравнение примет вид





Ответ: 
Пример 10. Решить уравнение 
Решение
Преобразуем уравнение:


Получим совокупность уравнений:

Ответ: 
Пример 11. Решить уравнение  .
.
Решение
Преобразуем уравнение, используя формулу  , получим:
, получим:
 .
.
Полученное уравнение равносильно совокупности уравнений:

Ответ: 
Пример 12. Решить уравнение 
Решение
Преобразуем уравнение: 

Полученное уравнение равносильно совокупности уравнений:

Второе уравнение совокупности  решений не имеет, поскольку
решений не имеет, поскольку 
Первое уравнение решим как однородное. Разделим обе его части на 
 в противном случае, из уравнения, получим, что и
в противном случае, из уравнения, получим, что и  что невозможно). В результате деления на
что невозможно). В результате деления на  , приходим к уравнению:
, приходим к уравнению:

Ответ: 
Пример 13. Решите уравнение  .
.
Решение
Преобразуем уравнение:


 .
.
Это уравнение равносильно совокупности уравнений:

Ответ: 
Пример 14. Решить уравнение  .
.
Решение
Преобразуем уравнение:  . Применим тождество преобразования суммы синусов в произведение:
. Применим тождество преобразования суммы синусов в произведение:  .
.
Учитывая, что cosx функция четная, получим:  .
.
Уравнение примет вид:  .
.
Это уравнение равносильно совокупности уравнений:

 .
.
Ответ:  .
.
Пример 15. Решите уравнение  .
.
Решение
Преобразуем уравнение, применяя тождество понижения порядка
 , получим:
, получим:




Ответ: 
Пример 16. Решите уравнение
 .
.
Решение
Преобразуем произведение функций в сумму, получим






Ответ: 
Пример 17. Решите уравнение
 .
.
Решение
Преобразуем уравнение, применяя формулы приведения:


 .
.
Ответ:  .
.
Пример 18. Решите уравнение 
Решение
Область допустимых значений: 

Преобразуем уравнение, заменив 1 на  и преобразуя разность синусов, в правой части уравнения, в произведение. Тангенс, заменим на частное от деления синуса на косинус.
и преобразуя разность синусов, в правой части уравнения, в произведение. Тангенс, заменим на частное от деления синуса на косинус.








Отсюда находим 

Задание 1
Решите уравнения
27.  . 28.
. 28.  .
.
29.  .
.
30.  31.
31.  .
.
32.  33.
33.  .
.
34.  . 35.
. 35.  .
.
36.  . 37.
. 37.  .
.
Задание 2
Решите уравнения.
58.  . 59.
. 59.  .
.
60.  . 61.
. 61.  .
.
62.  . 63.
. 63.  .
.
64.  . 65.
. 65.  .
.
66.  . 67.
. 67. 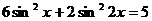 .
.
68.  . 69.
. 69.  .
.
70.  .
.
71.  . 72.
. 72.  .
.
73.  . 74.
. 74.  .
.
75. 
3. Уравнения, однородные относительно  и
и 
Определение. Рассмотрим уравнение вида

где  - действительные числа. В каждом слагаемом левой части уравнения (1) степени одночленов равны n, т. е. сумма степеней синуса и косинуса одна и та же и равна n. Такое уравнение называется однородным относительно
- действительные числа. В каждом слагаемом левой части уравнения (1) степени одночленов равны n, т. е. сумма степеней синуса и косинуса одна и та же и равна n. Такое уравнение называется однородным относительно  и
и  , а число n называется показателем однородности.
, а число n называется показателем однородности.
Ясно, что если  , то уравнение примет вид:
, то уравнение примет вид:
 решениями которого являются значения x, при которых
решениями которого являются значения x, при которых  , т. е. числа
, т. е. числа  . Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
. Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
Если же  , то эти числа не являются корнями уравнения (1).
, то эти числа не являются корнями уравнения (1).
При  получим:
получим:  ,
,  и левая часть уравнения (1) принимает значение
и левая часть уравнения (1) принимает значение  .
.
Итак, при  ,
,  и
и  , поэтому можно разделить обе части уравнения на
, поэтому можно разделить обе части уравнения на  . В результате получаем уравнение:
. В результате получаем уравнение:

которое, подстановкой  легко сводится к алгебраическому:
легко сводится к алгебраическому:
 .
.
1. Однородные уравнения с показателем однородности 1. При  имеем уравнение
имеем уравнение  .
.
Если  , то это уравнение равносильно уравнению
, то это уравнение равносильно уравнению  ,
,  ,
,
откуда  .
.
Пример 76. Решите уравнение  .
.
Решение
Это уравнение однородное первой степени 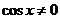 . Разделим обе его части на
. Разделим обе его части на  получим:
получим:  .
.
Ответ:  .
.
Пример 77. При  получим однородное уравнение вида
получим однородное уравнение вида
 .
.
Решение
Если  , тогда разделим обе части уравнения на
, тогда разделим обе части уравнения на 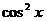 , получим уравнение
, получим уравнение  , которое подстановкой
, которое подстановкой  легко приводится к квадратному:
легко приводится к квадратному:  . Если
. Если  , то уравнение имеет действительные корни
, то уравнение имеет действительные корни  . Исходное уравнение будет иметь две группы решений:
. Исходное уравнение будет иметь две группы решений:  .
.
Если  , то уравнение не имеет решений.
, то уравнение не имеет решений.
Пример 78. Решите уравнение  .
.
Решение
Это уравнение однородное второй степени. Разделим обе чести уравнения на 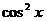 , получим:
, получим:  . Пусть
. Пусть  , тогда
, тогда  ,
,  ,
,  .
.  .
.
Ответ:  .
.
3. К уравнению вида (1) сводится уравнение

Для этого достаточно воспользоваться тождеством 
В частности, уравнение  сводится к однородному, если заменить d на
сводится к однородному, если заменить d на  , тогда получим равносильное уравнение:
, тогда получим равносильное уравнение: 
 .
.
Пример 79. Решите уравнение  .
.
Решение
Преобразуем уравнение к однородному:

 .
.
Разделим обе части уравнения на  , получим уравнение:
, получим уравнение:
 . Пусть
. Пусть  , тогда приходим к квадратному уравнению:
, тогда приходим к квадратному уравнению:  .
.
 .
.
Ответ:  .
.
Пример 80. Решите уравнение  .
.
Решение
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения:  ,
,

 .
.
Пусть  , тогда получим
, тогда получим  .
.
 .
.
Ответ:  .
.
Пример 81. Решите уравнение 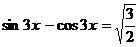 .
.
Решение
Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения:  ,
,

 .
.
Получили однородное уравнение:  .
.
Пусть  ,
,
 ,
,
 .
.
Ответ:  ,
,  .
.
I-й способ
Преобразуем уравнение, используя формулы приведения, получим:
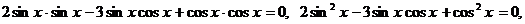
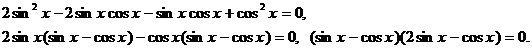
Получим совокупность уравнений:
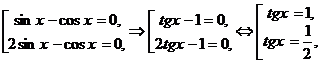
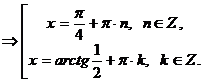
Ответ: 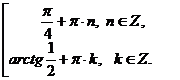
II-й способ
Применим формулы приведения:
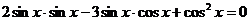 - это однородное уравнение второй степени,
- это однородное уравнение второй степени, 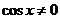 .
.
Разделим обе части уравнения на 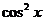 ,
, 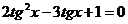 .
.
Пусть tgx = t, тогда получим: 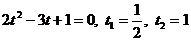 .
.
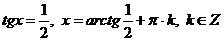 ,
, 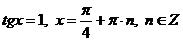 .
.
Ответ: 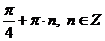 ;
; 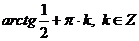 .
.
Пример 84. Решить уравнение 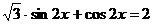 .
.
Решение
Преобразуем уравнение к однородному:
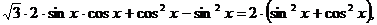
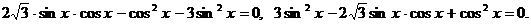
Полученное уравнение - однородное. Разделим обе части этого уравнения на 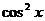 (
( 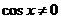 , ибо, в противном случае, из уравнения следует, что и
, ибо, в противном случае, из уравнения следует, что и 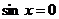 , что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество
, что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество 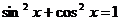 ). В результате деления на
). В результате деления на 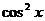 , получим:
, получим: 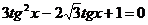 .
.
Положим 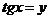 , получим
, получим 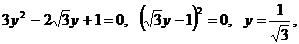
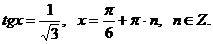
Ответ: 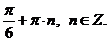
Пример 85. Решить уравнение 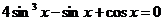 .
.
Решение
Это уравнение не является однородным. Перепишем его иначе:
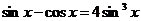 . Умножим левую часть уравнения на 1, а точнее на её значение
. Умножим левую часть уравнения на 1, а точнее на её значение 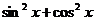 . После приведения подобных слагаемых имеем:
. После приведения подобных слагаемых имеем:
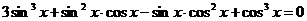 . Это однородное уравнение третьей степени относительно sinx и cosx,
. Это однородное уравнение третьей степени относительно sinx и cosx, 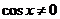 . Если cosx = 0, то из уравнения следует sinx=0, что невозможно.
. Если cosx = 0, то из уравнения следует sinx=0, что невозможно.
Разделим обе части уравнения на 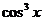 , получим:
, получим: 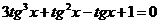 .
.
Положим tgx = y, получим 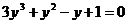 . Нетрудно заметить, что y = -1 является корнем уравнения. Разделим левую часть на y + 1, получим:
. Нетрудно заметить, что y = -1 является корнем уравнения. Разделим левую часть на y + 1, получим:
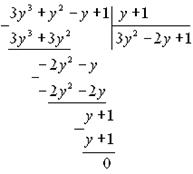
Уравнение примет вид: 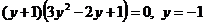 .
.
Уравнение 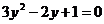 не имеет корней, так как дискриминант трехчлена отрицателен.
не имеет корней, так как дискриминант трехчлена отрицателен. 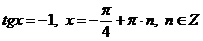 .
.
Ответ: 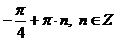
Пример 86. Решить уравнение 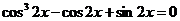 .
.
Решение
I-й способ
Преобразуем уравнение:
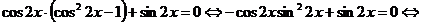
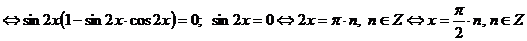 ;
;
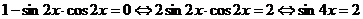 - решений не имеет.
- решений не имеет.
Ответ: 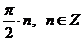 .
.
II-й способ
Преобразуем уравнение: 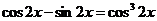 . Умножим левую часть уравнения на
. Умножим левую часть уравнения на 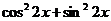 , получим:
, получим: 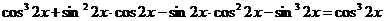 .
.
После приведения подобных слагаемых получим однородное уравнение третьей степени относительно sinx и cosx: 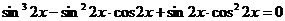 ,
, 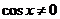 .
.
Разделим обе части уравнения на 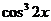 , получим:
, получим: 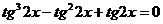 .
.
Пусть tgx = y, тогда 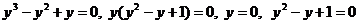 - не имеет корней.
- не имеет корней.
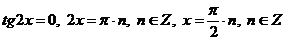 .
.
Ответ:  .
.
Пример 87. Решить уравнение 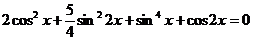 .
.
Решение
Преобразуем уравнение: 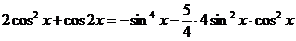 ,
,
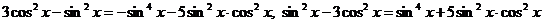 ,
,
Умножим левую часть уравнения на 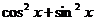 , получим:
, получим:
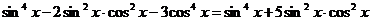 ,
,
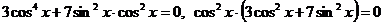 ,
,
Последнее уравнение - однородное четвертой степени относительно sinx и cosx.
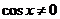 . Если допустить, что cosx = 0, тогда из уравнения следует sinx = 0, что невозможно. Разделим обе части уравнения на
. Если допустить, что cosx = 0, тогда из уравнения следует sinx = 0, что невозможно. Разделим обе части уравнения на 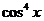 ,
, 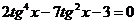 .
.
Пусть 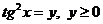 , получим квадратное уравнение:
, получим квадратное уравнение: 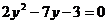 ,
,
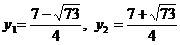 .
. 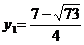 - не удовлетворяет условию
- не удовлетворяет условию 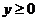 и является посторонним корнем.
и является посторонним корнем.
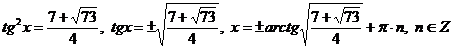
Ответ: 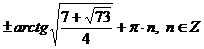 .
.
Задание 3
88. 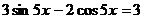 . 89.
. 89. 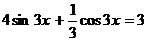 .
.
90. 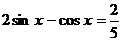 . 91.
. 91. 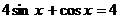 .
.
92. 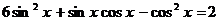 . 93.
. 93. 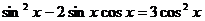 .
.
94. 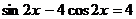 . 95.
. 95. 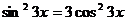 .
.
96. 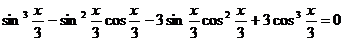 .
.
97. 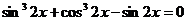 . 98.
. 98. 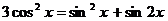 .
.
99. 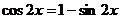 . 100.
. 100. 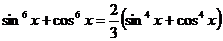 .
.
101. 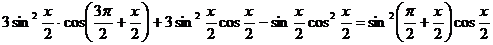 .
.
102. 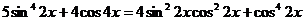 .
.
103. 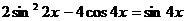 . 104.
. 104. 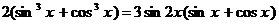 .
.
4. Для преобразования уравнений было использовано основное тригонометрическое тождество 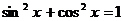 . Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.
. Это тождество не только позволяет сводить некоторые уравнения к однородным, но и в некоторых случаях дает возможность найти более простые решения таких уравнений. Для этой цели используются тождества, получаемые с помощью основного тригонометрического тождества.
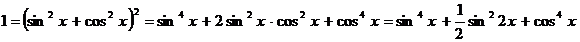 ,
,
отсюда находим 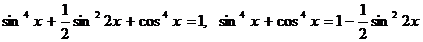 .
.

Далее,
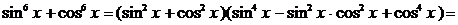
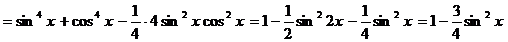 .
.

Преобразуем сумму 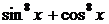 , используя формулу (4).
, используя формулу (4).
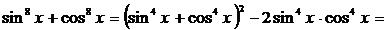
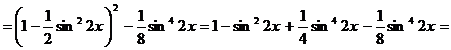
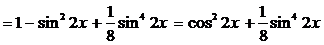 .
.
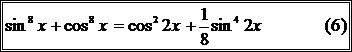
Выше приведенные формулы очень часто используются при решении тригонометрических уравнений, и не только однородных.
Пример 105. Решите уравнение
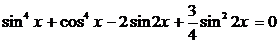 .
.
Решение
Преобразуем уравнение, используя формулу (4): 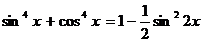 , получим уравнение:
, получим уравнение: 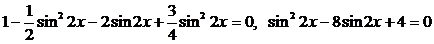 .
.
Пусть 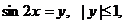 приходим к квадратному уравнению:
приходим к квадратному уравнению:
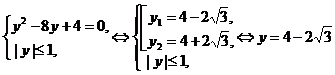 ,
,
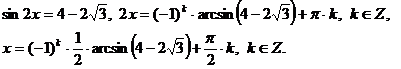
Ответ: 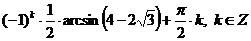 .
.
Пример 106. Решите уравнение
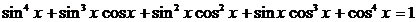 .
.
Решение
Преобразуем уравнение, используя формулу (4): 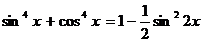 , получим уравнение:
, получим уравнение: 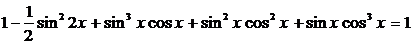 ,
,
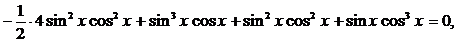

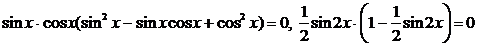 ,
,
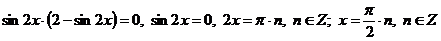 .
.
Уравнение 2 - sin2x = 0, sin2x = 2 не имеет решений.
Ответ:  .
.
Пример 107. Решите уравнение 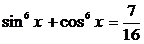 .
.
Решение
Преобразуем уравнение, используя формулу: 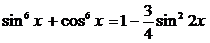 , получим:
, получим: 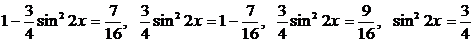
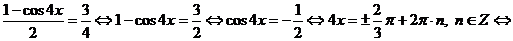
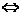
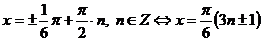 .
.
Ответ: 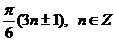 .
.
Пример 108. Решите уравнение 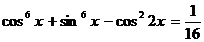 .
.
Решение
Преобразуем уравнение, используя формулу: 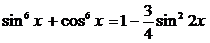 , получим:
, получим:
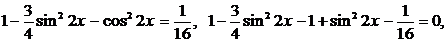
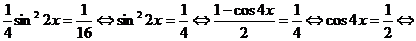 .
.