Методические указания, контрольные работы
МЕТОДИЧЕСКИЕ УКАЗАНИЯ, КОНТРОЛЬНЫЕ РАБОТЫ
ПО дИСЦИПЛИНЕ «Математика»
(1 семестр)
для студентов специальности 190601.65 (150200)
«Автомобили и автомобильное хозяйство»
 |
Волгоград 2010
УДК 519.2
Рецензент:
канд. пед. наук Ребро И. В.
Антипина С. Г. Методические указания, контрольные работы по дисциплине «Математика» (1 семестр)/ С. Г. Антипина; ВПИ (филиал) ВолгГТУ. – Волгоград, 2010. – 52 с.: илл.
Методические указания предназначены для студентов заочной формы обучения высших технических учебных, специальности 190601.65 (150200)
«Автомобили и автомобильное хозяйство». Содержит решения типовых примеров, задания для контрольной работы.
Библиогр.: 8 наименований
Ó Волгоградский государственный
технический университет, 2010
Ó Волжский политехнический
институт, 2010
Оглавление
| Оглавление | |
| Правила выполнения и оформления контрольных работ | |
| Контрольные работы | |
| Типовой разбор варианта контрольной работы | |
| Список литературы | |
| Вопросы к экзамену | |
| Приложения: | |
| Векторы | |
| Прямая на плоскости | |
| Кривые второго порядка на плоскости | |
| Плоскость и прямая в пространстве | |
| Поверхности второго порядка | |
| Дифференциальное исчисление функции одной переменной |
Правила выполнения и оформления
Контрольных работ
При выполнении контрольных работ необходимо придерживаться указанных ниже правил. Работы, выполненные без их соблюдения, не засчитываются и возвращаются студенту для переработки.
1.Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 2-3 см для замечаний рецензента.
2.В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер – последняя цифра в зачетке, название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отправки работы в институт и адрес студента.
3.В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не засчитываются.
4.Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5.Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6.Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7.После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Вариант 0.
Контрольная работа №2 «Введение в анализ. Дифференциальное
Вариант 1.
Контрольная работа №2 «Введение в анализ.
Вариант 2.
Контрольная работа №2 «Введение в анализ.
Вариант 3.
Контрольная работа №2 «Введение в анализ.
Вариант 4.
Контрольная работа №2 «Введение в анализ.
Вариант 5.
Контрольная работа №2 «Введение в анализ.
Вариант 6.
Контрольная работа №2 «Введение в анализ.
Вариант 7.
Контрольная работа №2 «Введение в анализ.
Вариант 8.
Вариант 9.
Контрольная работа №1
1)Даны матрицы: 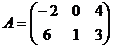 ,
, 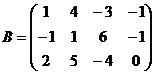 ,
, 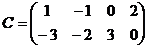 .
.
Найти 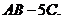
Решение:
Матрица А имеет размерность 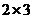 , матрица В размерность
, матрица В размерность 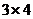 . Т.к. число столбцов первой матрицы равно числу строк второй матрицы, то данные матрицы можно перемножить. В результате получится некоторая матрица D, имеющая размерность
. Т.к. число столбцов первой матрицы равно числу строк второй матрицы, то данные матрицы можно перемножить. В результате получится некоторая матрица D, имеющая размерность 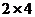 .
.
Найдем элементы матрицы D:
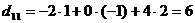 ;
; 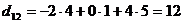 ;
; 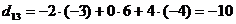 ;
; 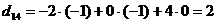 ;
;
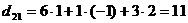 ;
; 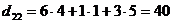 ;
; 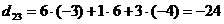 ;
; 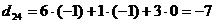 .
.
Тогда 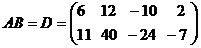 .
.
По правилу умножения матрицы на число 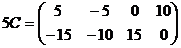
Найдём 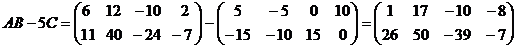 .
.
2)Дана матрица: 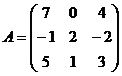 . Найти обратную к ней матрицу
. Найти обратную к ней матрицу 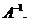
Решение:
Вычислим определитель матрицы А методом треугольников:
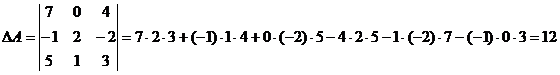
Т.к. 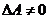 , то обратная матрица может быть найдена. Найдём алгебраические дополнения для всех элементов матрицы А:
, то обратная матрица может быть найдена. Найдём алгебраические дополнения для всех элементов матрицы А:
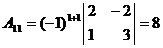 | 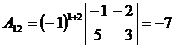 | 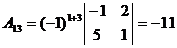 |
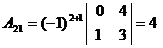 | 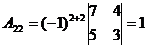 | 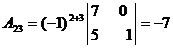 |
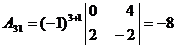 | 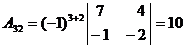 | 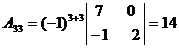 . . |
Составим присоединённую матрицу 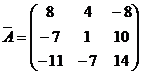
Обратная матрица 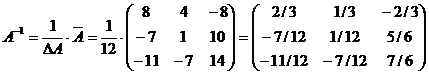
Для проверки, правильности вычисления 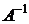 , найдём
, найдём
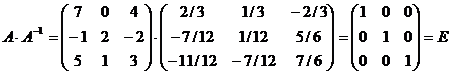
3) Решить систему методом Жордана – Гаусса:
a) 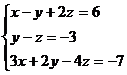
Решение:
Рассмотрим расширенную матрицу системы: 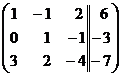 . Приведём её к верхне- треугольному виду.
. Приведём её к верхне- треугольному виду.
Из 3-ей стоки вычтем 1-ю строку, умноженную на 3: 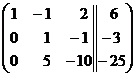 .
.
Разделим 3-ю строку на 5: 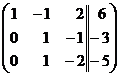
Вычтем из 3-ей строки 2-ю строку: 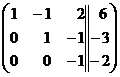 и разделим 3-ю строку
и разделим 3-ю строку
на (-1): 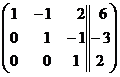 . Мы привели матрицу к верхнее- треугольному виду.
. Мы привели матрицу к верхнее- треугольному виду.
Заменим исходную систему системой, полученной путём преобразования матрицы и найдем значения переменных: 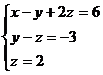
Из 2-го уравнения при 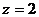 получим
получим 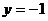 .Подставляя значения y и z в 1-ое уравнение найдем значение
.Подставляя значения y и z в 1-ое уравнение найдем значение 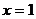 .Тогда решение системы может быть представлнно в виде матрицы-столбца:
.Тогда решение системы может быть представлнно в виде матрицы-столбца: 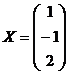 .
.
b) 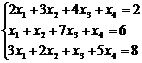
Решение:
Рассмотрим расширенную матрицу системы: 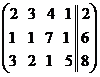 . Приведём её к верхнее треугольному виду.
. Приведём её к верхнее треугольному виду.
Поменяем местами 1-ю и 2-ю строки: 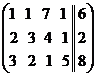 . Из 2-ой стоки вычтем 1-ю строку, умноженную на 2, из 3-ей стоки вычтем 1-ю строку, умноженную на 3:
. Из 2-ой стоки вычтем 1-ю строку, умноженную на 2, из 3-ей стоки вычтем 1-ю строку, умноженную на 3: 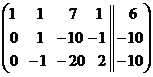 . К 3-ей строке прибавим 2-ю строку:
. К 3-ей строке прибавим 2-ю строку: 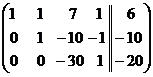 . Третью строку разделим на (-30):
. Третью строку разделим на (-30): 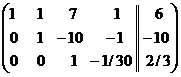 . Переменные
. Переменные 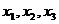 являются базисными, а переменная
являются базисными, а переменная 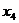 является свободной. Заменим исходную систему системой, полученной путём преобразования матрицы и выразим базисные переменные через свободные:
является свободной. Заменим исходную систему системой, полученной путём преобразования матрицы и выразим базисные переменные через свободные: 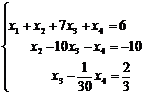 . Выразим из 3-го уравнения
. Выразим из 3-го уравнения 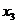 и подставим его значение во второе уравнение, затем из 2-го уравнения выразим
и подставим его значение во второе уравнение, затем из 2-го уравнения выразим 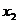 и подставим в 1-е уравнение. Тогда система примет вид:
и подставим в 1-е уравнение. Тогда система примет вид: 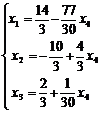 . Свободная переменная
. Свободная переменная 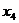 может принимать любые значения. Зададим
может принимать любые значения. Зададим 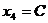 , где С- произвольная константа. Тогда решение системы может быть представлнно в виде матрицы-столбца:
, где С- произвольная константа. Тогда решение системы может быть представлнно в виде матрицы-столбца: 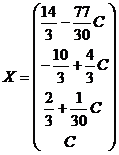 .
.
4) Даны векторы 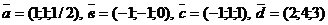 .
.
a)Доказать, что вектора 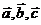 образуют базис и найти разложение вектора
образуют базис и найти разложение вектора 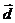 по этому базису.
по этому базису.
b) Найти скалярное произведение векторов 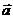 и
и 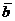 .
.
c) Найти векторное произведение векторов 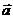 и
и 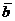 .
.
d) Найти смешанное произведение векторов 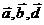 .
.
Решение:
a) Три вектора в трёхмерном пространстве образуют базис, если они линейно независимы. Для проверки линейной зависимости векторов составим их нулевую линейную комбинацию: 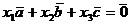 . Данное векторное уравнение соответствует системе трёх линейных однородных уравнений:
. Данное векторное уравнение соответствует системе трёх линейных однородных уравнений: 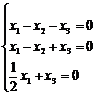 . Вычислим определитель матрицы, полученной системы:
. Вычислим определитель матрицы, полученной системы: 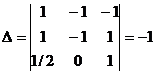 .
.
Т.к. определитель основной матрицы однородной системы 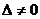 , то система имеет единственное нулевое решение
, то система имеет единственное нулевое решение 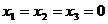 . Следовательно, по определению линейной зависимости векторов, векторы
. Следовательно, по определению линейной зависимости векторов, векторы 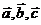 являются линейно независимыми , а значит образуют базис.
являются линейно независимыми , а значит образуют базис.
Найдём разложение вектора 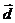 по этому базису. Составим линейную комбинацию:
по этому базису. Составим линейную комбинацию: 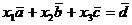 . Перепишем данное векторное уравнение в координатной форме:
. Перепишем данное векторное уравнение в координатной форме: 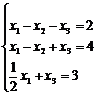 . Решая полученную систему (например, методом Крамера), найдём
. Решая полученную систему (например, методом Крамера), найдём 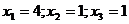 . Следовательно, разложение вектора
. Следовательно, разложение вектора 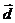 по базису
по базису 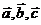 имеет вид:
имеет вид: 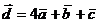 .
.
b) 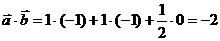 .
.
c) 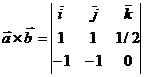 Раскрывая определитель по элементам 1-ой строки, получим:
Раскрывая определитель по элементам 1-ой строки, получим: 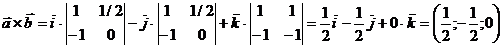 .
.
d) 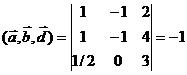 .
.
5) Даны координаты вершин треугольника, A(3, 5), B(-7, 12), C(2, -6). Найти:
a) длину стороны AB;
b) общие уравнения сторон AB и BC;
c) величину угла B;
d)длину и уравнение высоты, опущенной из вершины 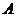 ;
;
e) площадь треугольника 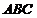 ;
;
f) уравнение прямой, проходящей через точку 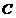 параллельно стороне
параллельно стороне 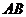 .
.
Решение:
a)Найдём длину стороны AB, как длину вектора 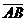 :
: 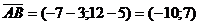 .
. 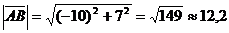 .
.
b)Найдём уравнения сторон AB и BCпо формуле уравнения прямой, проходящей через две точки.
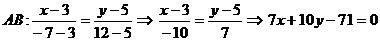 - общее уравнение прямой АВ.
- общее уравнение прямой АВ.
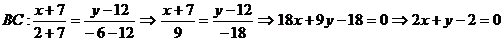 - общее уравнение прямой ВС.
- общее уравнение прямой ВС.
 c) Угол В – есть угол между прямыми AB и BC. Угол между прямыми может быть найден, как угол между их нормальными векторами.
c) Угол В – есть угол между прямыми AB и BC. Угол между прямыми может быть найден, как угол между их нормальными векторами. 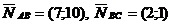 .
. 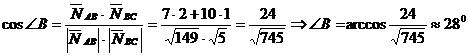 .
.
d) Опустим высоту из точки А на сторону ВС. Пусть точка D – есть основание этой высоты. Прямая AD перпендикулярна прямой ВС. Следовательно, вектор нормали прямой ВС является направляющим вектором для прямой AD. 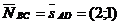 . Воспользуемся каноническим уравнением прямой.
. Воспользуемся каноническим уравнением прямой. 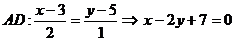 - общее уравнение высоты AD.
- общее уравнение высоты AD.
Найдём длину высоты AD, как расстояния от точки А до прямой ВС.
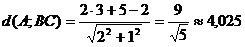 .
.
e)Найдём площадь треугольника 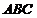 как половину произведения длины основания треугольника на его высоту.
как половину произведения длины основания треугольника на его высоту.
Пусть ВС – основание 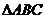 , AD – его высота.
, AD – его высота.
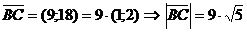 ;
; 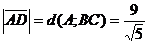 .
.
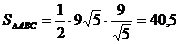 .
.
f) Обозначим прямую, проходящую через точку 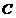 параллельно стороне
параллельно стороне 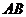 через l. Т.к.
через l. Т.к. 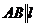 , то
, то 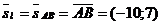 . Составим каноническое уравнение прямой l.
. Составим каноническое уравнение прямой l.
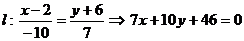 - общее уравнение прямой l.
- общее уравнение прямой l.
6) Даны четыре точки A(3;-2;1), B(1;2;4), C(-5;4;6), M(2;3;-1). Найти:
a)уравнение плоскости a, проходящей через три точки A, B, C;
b)каноническое уравнения прямой AB;
c)уравнение и длину высоты, опущенной из вершины М на грань 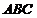 ;
;
d) объем пирамиды АВСМ.
Решение:
a)Воспользуемся уравнением плоскости, проходящей через три точки: 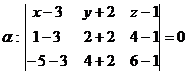
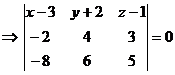
Разложим определитель по элементам первой строки:
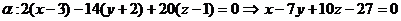 - общее уравнение плоскости α.
- общее уравнение плоскости α.
b) Воспользуемся уравнением прямой, проходящей через две точки:
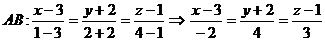 - каноническое уравнение прямой АВ.
- каноническое уравнение прямой АВ.
c) Обозначим высоту, опущенной из вершины М на грань 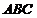 через l. Т.к
через l. Т.к 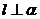 , то
, то 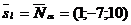 . Составим каноническое уравнение прямой l:
. Составим каноническое уравнение прямой l: 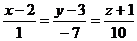 .
.
Найдём длину высоты как расстояние от точки М до плоскости α: 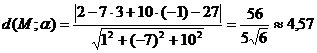 .
.
d)Объём пирамиды равен 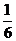 объёма параллелепипеда, построенного на трёх векторах и может быть вычислен через смешанное произведение этих векторов:
объёма параллелепипеда, построенного на трёх векторах и может быть вычислен через смешанное произведение этих векторов: 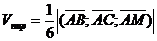 .
.
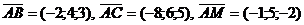
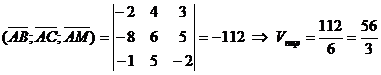 .
.
7) Дано уравнение кривой второго порядка 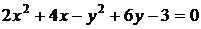 . Привести её к каноническому виду, определить вид, указать её параметры.
. Привести её к каноническому виду, определить вид, указать её параметры.
Решение:
Приведём данное уравнение к каноническому виду. Для этого выделим полные квадраты для переменных x и y:
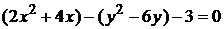 ,
,
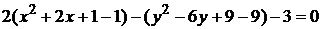 ,
,
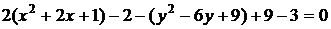 ,
,
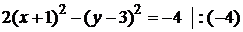 .
.
Таким образом, получили каноническое уравнение гиперболы со смещённым центром:
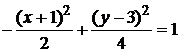 или
или 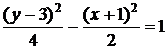 .
.
Точка 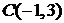 – центр гиперболы.
– центр гиперболы.
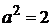

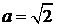 – мнимая полуось;
– мнимая полуось;
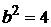

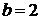 – действительная полуось;
– действительная полуось;
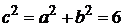

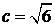 ;
;
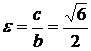 – эксцентриситет.
– эксцентриситет.
Точки 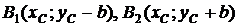 определяют вершины гиперболы:
определяют вершины гиперболы:
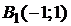 ,
, 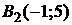 .
.
Точки 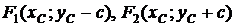 определяют фокусы гиперболы:
определяют фокусы гиперболы:
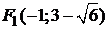 ,
, 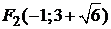 .
.
Уравнения 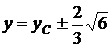 определяют директрисы гиперболы:
определяют директрисы гиперболы: 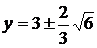 .
.
Уравнения 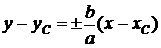 определяют асимптоты:
определяют асимптоты: 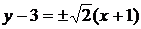 .
.
Начертим гиперболу 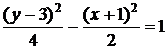 , используя найденные параметры (рис. 1).
, используя найденные параметры (рис. 1).
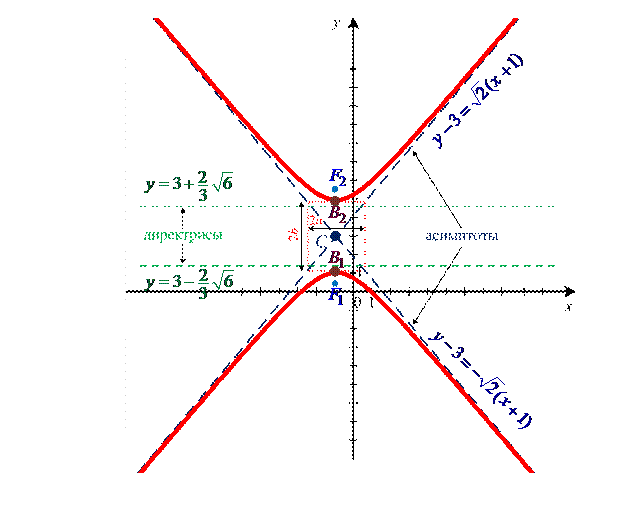
Рис. 1
Контрольная работа №2
1)Вычислить пределы, не пользуясь правилом Лопиталя.
Решение:
a) 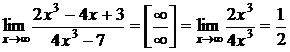 . Предел отношения многочленов и иррациональностей при
. Предел отношения многочленов и иррациональностей при 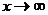 равен пределу отношения старших по степени слагаемых.
равен пределу отношения старших по степени слагаемых.
b) 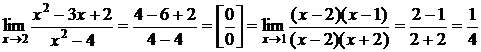 .
.
c) 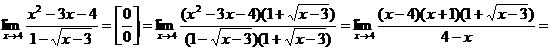
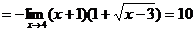 .
.
d) 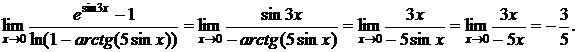
e)Воспользуемся обобщённой формулой второго замечательного предела:
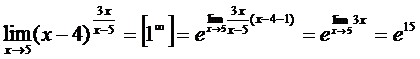 .
.
2) Исследовать функции на непрерывность. Классифицировать точки разрыва.
a) 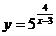 .
.
Решение:
Т.к. при 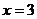 знаменатель дроби
знаменатель дроби 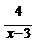 обращается в ноль, то
обращается в ноль, то 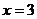 -есть точка разрыва данной функции. Найдём пределы при
-есть точка разрыва данной функции. Найдём пределы при 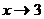 слева и справа.
слева и справа.
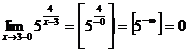 ,
, 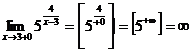 , следовательно
, следовательно 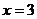 -есть точка разрыва второго рода.
-есть точка разрыва второго рода.
b) 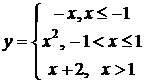
Решение:
Функции 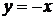 ,
, 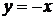 ,
, 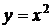 – элементарные и в области определения непрерывны. Точки разрыва возможны в переходных от одного задания к другому точках, т.е. в точках
– элементарные и в области определения непрерывны. Точки разрыва возможны в переходных от одного задания к другому точках, т.е. в точках 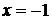 и
и 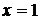 . Исследуем поведение функции в этих точках:
. Исследуем поведение функции в этих точках:
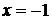 слева:
слева: 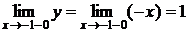 справа:
справа: 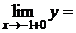
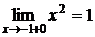 , тогда
, тогда 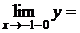
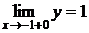 , т.е. функция непрерывна в точке
, т.е. функция непрерывна в точке 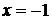
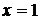 слева:
слева: 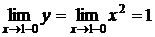 справа:
справа: 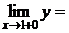
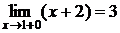 , тогда
, тогда 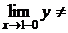
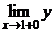 , т.е. функция имеет разрыв первого рода в точке
, т.е. функция имеет разрыв первого рода в точке 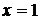 , т.к. пределы конечны.
, т.к. пределы конечны.
3) Найти производные первого порядка для следующих функций:
a) 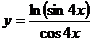
Решение:
Воспользуемся формулой для нахождения производной частного:
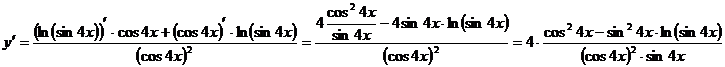 b)
b) 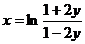
Решение:
Воспользуемся формулой для нахождения производной обратной функции:
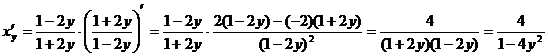
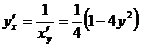
c) 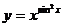
Решение:
Воспользуемся формулой логарифмического дифференцирования.
Найдём 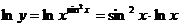
По формуле для нахождения производной от произведения:
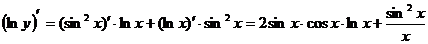 .
.
Следовательно 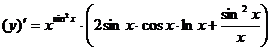 .
.
d) 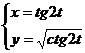
Решение:
Воспользуемся формулой для нахождения производной параметрически заданной функции: 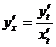 .
.
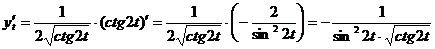
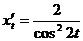 ;
;
Тогда 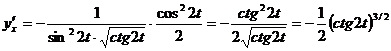 .
.
4) Найти уравнения касательной и нормали к графику функции 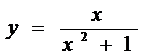
в точке x0=-2.
Решение:
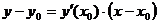 - уравнение касательной.
- уравнение касательной.
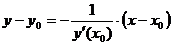 - уравнение нормали.
- уравнение нормали.
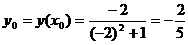 ;
;
По формуле для нахождения производной частного:
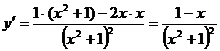 ;
; 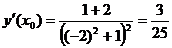 .
.
Тогда уравнение касательной: 
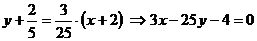 ;
;
Уравнение нормали: 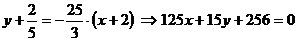 .
.
5) С помощью методов дифференциального исчисления построить график функции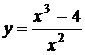 .
.
Решение:
1) Области определения функции не принадлежит только точка х=0:
D(y)=(-¥;0)È(0;+¥).
2) 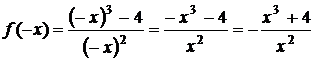
 функция общего вида (не чётная и не нечётная).
функция общего вида (не чётная и не нечётная).
Функция не периодична потому, что её область определения не имеет периодической структуры.
3)Найдём точки пересечения графика с осями координат.
С осью Ox: у=0, 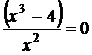

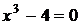 ,
, 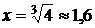
 точка
точка 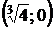 .
.
С осью Oy: при х=0 функция не существует  точек пересечения с осью Oy нет.
точек пересечения с осью Oy нет.
4)Найдем асимптоты функции.
Вертикальные:
Исследуем функцию в окрестности точки разрыва х=0.
Левосторонний предел 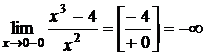 .
.
Правосторонний предел равен 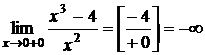

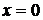 -двусторонняя вертикальная асимптота.
-двусторонняя вертикальная асимптота.
Наклонные и горизонтальные:
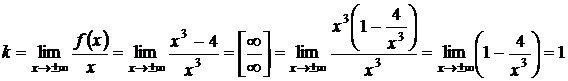
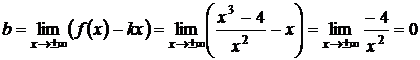

y=х – прямая, которая служит наклонной асимптотой графика как при x®-¥, так и при x®+¥.
5) Найдем критические точки: 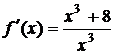

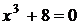
 х=-2.
х=-2.
Найдем интервалы монотонности (метод интервалов) и точки экстремума функции.
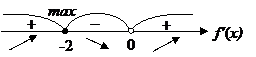
Интервалы монотонности: на интервале 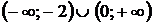 функция возрастает; на интервале
функция возрастает; на интервале 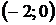 функция убывает.
функция убывает.
При х=-2- функция принимает максимальное значение 
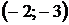 точка максимума.
точка максимума.
При х=0 – экстремума нет, так как в этой точке функция не определена.
6) Исследуем функцию на вогнутость, выпуклость и перегиб.
Найдём вторую производную 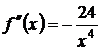 .
.
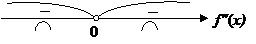
Интервалы выпуклости, вогнутости: на интервале 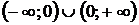 функция выпукла. Перегибов нет.
функция выпукла. Перегибов нет.
7) На рис.2 построена кривая, удовлетворяющая проведённому исследованию.
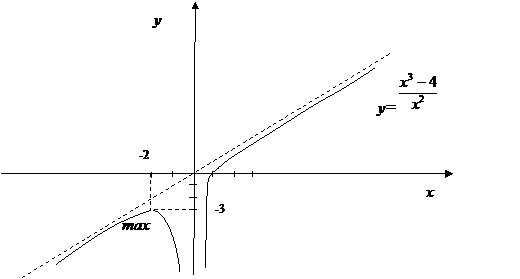
Рис. 2
6)Найти наибольшее и наименьшее значения функции 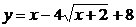
на отрезке 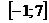 .
.
Решение:
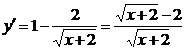 . Найдём критические точки:
. Найдём критические точки:
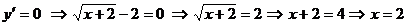
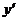 не существует, если
не существует, если 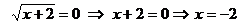
Точка 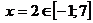 ,
, 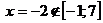 .
.
Найдём 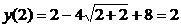 .
.
Найдём значения функции на концах отрезка:
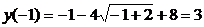 ;
; 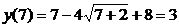 .
.
Наибольшее значение на данном отрезке достигается функцией в двух точках – на концах отрезка: 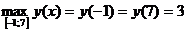 .
.
Наименьшее значение на данном отрезке достигается функцией во внутренней точке отрезка: 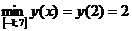 .
.
7)Даны функция 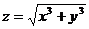 и точки A(1; 2), B(1,02; 1,97).
и точки A(1; 2), B(1,02; 1,97).
Вычислить
a) значение функции 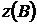 ;
;
b) 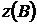 с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
с помощью дифференциала, заменяя приращение при переходе от A к B дифференциалом. Оценить в процентах относительную погрешность вычисления.
c) Составить уравнения касательной плоскости и нормали к поверхности ,заданной данной функцией в точке C (x0, y0, z0).
Решение:
a) 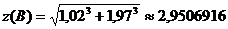 .
.
b) Воспользуемся формулой: 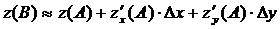 .
.
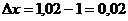 ;
; 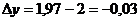 ;
; 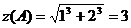 .
.
Найдем 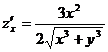 ,
, 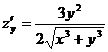 , тогда
, тогда 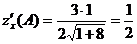 ,
, 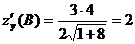 .
.
Следовательно, получим: 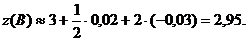
Оценим относительную погрешность вычисления: 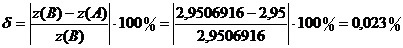 .
.
c) C (1; 2; 3)
Составим уравнение касательной плоскости : 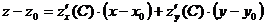
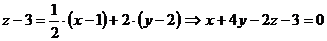
Составим уравнение нормали: 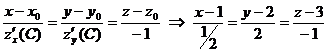 .
.
8) Даны функция 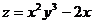 , точка A(2;-1) и вектор
, точка A(2;-1) и вектор 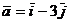 . Требуется найти
. Требуется найти 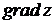 и производную в точке A по направлению вектора
и производную в точке A по направлению вектора 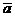 .
.
Решение:
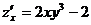 ;
; 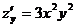 ;
; 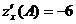 ;
; 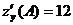
Следовательно 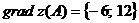 .
.
Найдём направляющие косинусы вектора 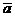 :
:
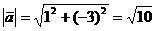 ;
; 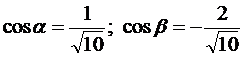 .
.
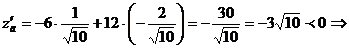 данная функция убывает в направлении вектора
данная функция убывает в направлении вектора 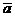
9) Найти экстремум функции 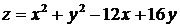 и ее наибольшее и наименьшее значения в области
и ее наибольшее и наименьшее значения в области 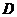 :
: 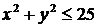 .
.
Решение:
Найдем стационарные точки функции из системы: 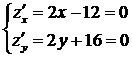 .
.
М(6; -8)- стационарная точка. 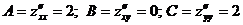 .
.
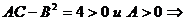 точка М0(6; -8) является точкой минимума функции.
точка М0(6; -8) является точкой минимума функции.
Стационарная точка М0 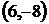 не лежит в заданном круге. Поэтому наибольшее и наименьшее значения функция принимает на границе области, т.е. на окружности
не лежит в заданном круге. Поэтому наибольшее и наименьшее значения функция принимает на границе области, т.е. на окружности 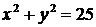 .
.
Составим функцию Лагранжа 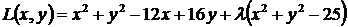 .
.
Ее стационарные точки найдем из системы 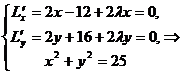
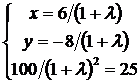 , откуда
, откуда 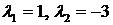 . Следовательно, стационарными точками границы являются М1(3, -4) и М2(-3, 4).
. Следовательно, стационарными точками границы являются М1(3, -4) и М2(-3, 4). 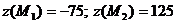 . Эти числа являются наименьшим и наибольшим значениями z в заданной области:
. Эти числа являются наименьшим и наибольшим значениями z в заданной области: 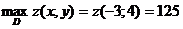 ;
; 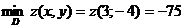 .
.
Список рекомендуемой литературы.
1. Агишева Д. К. Матрицы и их приложение к решению систем линейных уравнений: Учебное пособие/ Д. К. Агишева, С. А. Зотова, В. Б. Светличная. - Волгоград, РПК «Политехник», 2001. – 63с.
2. Александрова Л. А, Александрова В. А, Зотова С. А., Светличная В. Б., Матвеева Т. А., Короткова Н. Н. Математика. I часть: Учебное пособие (для студентов заочной формы обучения) / – Волгоград, РПК «Политехник», 2003. – 84с.
3. Письменный Д. Т. Конспект лекций по высшей математике. 1 часть. – М.: Рольф, 2000. – 288 с., с илл.
4. Данко П. Е.,Попов А. Г.,Коевникова Т. Я. Высшая математика в упранениях и задачах. Том 1 – М.: Высшая школа, 1980 – 320 с., с илл.
5. Зотова С. А., Светличная В. Б., Матвеева Т. А.. Практическое руководство по аналитической геометрии: Учебное пособие / – Волгоград, РПК «Политехник», 2003. – 41с.
6. Клетеник Д. В. Сборник задач по аналитической геометрии: Учебное пособие для втузов – СПб: «Специальная Литература», 1998.–200 с.: илл.
7. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1981.–720с.: илл.
8. Выгодский М. Я. Справочник по высшей математике. –М.: Гостехтеоргиздат, 1973.
Вопросы к экзамену по математике.
Аналитическая геометрия.
11. Прямая на плоскости. Виды уравнений прямых. Угол между прямыми. Условие параллельности, перпендикулярности двух прямых. Расстояние от точки до прямой.
12. Плоскость. Виды уравнений плоскостей. Угол между плоскостями. Условие параллельности, перпендикулярности двух плоскостей. Расстояние от точки до плоскости.
13. Прямая в пространстве. Виды уравнений прямых. Угол между прямыми. Угол между прямой и плоскостью. Условие параллельности, перпендикулярности, компланарности двух прямых.
14. Кривые второго порядка (эллипс, окружность, гипербола, парабола). Определение, канонические уравнения, характеристики.
Введение в анализ.
15. Функция. Область определения и область значений функции. Сложная, обратная, параметрически заданная функции.
16. Предел функции. Единственность предела функции в точке. Бесконечно малые (б.м.)и бесконечно большие(б.б.) функции. Свойства б.м. и б.б. функций.
17. Основные теоремы о пределах.
18. Замечательные пределы. Эквивалентные функции.
19. Односторонние пределы.
20. Непрерывность функции. Точки разрыва и их классификация.
Приложения
| ВЕКТОРЫ | |||
Координаты точки М есть координаты радиус-вектора 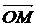 | 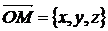 ; ; 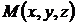 | ||
Вектор 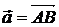 ; где ; где 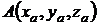 , , 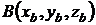 | 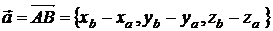 | ||
Вектор 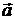 | 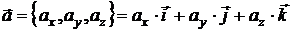 | ||
Длина вектора 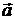 | 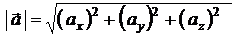 | ||
Орт 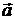 : : 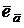 ( ( 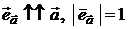 ) ) | 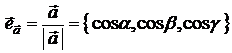 | ||
Направляющие косинусы 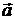 : : 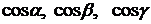 | 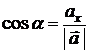 , , 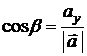 , , 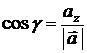 ; ; 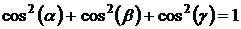 | ||
| Проекция вект |
