Решение СЛАУ методом Гаусса.
Нахождение множества решений системы линейных уравнений основывается на том, что от заданной системы с помощью элементарных преобразований строк переходят к равносильной системе, которая решается “проще”, чем исходная система.
Эквивалентными преобразованиями системы линейных уравнений являются:
1) перемена местами двух уравнений в системе;
2) умножение какого-либо уравнения системы на действительное число С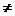 
0;
3) прибавление к одному уравнению другого уравнения, умноженного на произвольное число.
Метод Гаусса заключается в приведении расширенной матрицы данной системы элементарными преобразованиями строк к некоторому специальному виду - прямой ход схемы Гаусса, и нахождению затем множества решений системы с полученной расширенной матрицей, которая будет равносильна исходной. - обратный ход метода Гаусса.
Прямой ход метода Гаусса состоит в последовательном исключении неизвестных, а именно: в первом уравнении должны присутствовать все n неизвестных, во втором уравнении не должно присутствовать первое неизвестное 
; в третьем и 
и т.д., причем коэффициенты при неизвестных, с которых начинается каждое из уравнений, должны быть равны 1.
Любая матрица с помощью элементарных преобразований только строк может быть приведена к некоторому “ступенчатому” виду, а именно:
Здесь под “ступеньками”, которые начинаются в левом верхнем углу с элементов главной диагонали, все элементы равны нулю, над “ступеньками” могут быть любые числа, диагонали “ступенек” должны состоять только из 1, горизонтали “ступенек” могут образовываться любыми числами. Если матрицу исходной системы ( в расширенной матрице это соответствует элементам до вертикальной черты) удается привести к “треугольному” виду, а именно:
то система будет иметь единственное решение.
Если матрица совместной системы проводится к трапециевидному или ступенчатому виду, значит, система будет неопределенной, т.е. будет иметь бесчисленное множество решений.
Система не будет иметь решений, если в преобразованной матрице в последней ненулевой строке перед вертикальной чертой будут стоять все 0, что будет соответствовать уравнению 0=1, не имеющему решений.
Совместность СЛАУ. Т Кронекера-Капелли
Исследование систем линейных уравнений.
Матрица системы (1), дополненная справа столбцом свободных членов, называется расширенной матрицей системы (1):
Ранг матрицы А* либо равен рангу матрицы А либо на единицу больше.
Характер множества решений системы (1) зависит только от ранга матрицы А и от ранга расширенной матрицы А*.
Вопрос о совместности системы линейных уравнений полностью решается следующей теоремой.
Теорема Кронекера-Капелли.
Система линейных уравнений совместнатогда и только тогда, когда ранг расширенной матрицы А* равен рангу матрицы А.
Совместная система (1) тогда и только тогда обладает единственным решением, если ранг матрицы А равен числу неизвестных;
если rang А< n 
- система будет неопределенной.