Построение комплексных чисел.

ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ

Полагаем, что в произвольном подмножестве натуральных чисел всегда есть наименьшее.

Определение. Пусть a, bÎZ. Если существует qÎZ, что a = bq, то b делит a, или a делится на b, обозначаем b|a.

Простейшие свойства делимости:

1) Если a|b, b|c Þ a|c. Если a делит b и b делит c, то a делит c.

2) Если a,b,с и с не равно 0, то a делит b тогда и только тогда, когда ac делит bc, т. е. a|b; c¹0 Û ac|bc, a, b, cÎZ.

3) d|ai; i=1,…,n,x1,…,xnÎZ Þ d|a1 x1 +…+an xn.

4) a|b; b|a Þ a =±b.

Доказательство всех свойств однообразно: используется только определение делимости. Докажем:

4) a = bq и b = aq1 Þ a = aqq1 Þ a(qq1 – 1) = 0 Þ qq1 = 1, т. к. a¹0 Þ q = ±1.

Теорема (о делении с остатком).

Для любых a, bÎZ; b ¹ 0 существует единственная пара q, rÎZ такая, что a = bq+r, 0£ r<|b|.

Доказательство: Рассмотрим множество M = {a – bq, qÎZ}. Очевидно, что M∩{N, 0}¹Ø.

В любом таком множестве $ наименьшее r. Очевидно, что |b|>r ≥0.

Докажем единственность.

Пусть ещё a = bq1 + r1. Тогда вычитанием из первого второе получим

0 = b(q – q1) + r – r1. Отсюда следует, что r – r1 кратно b, но |r – r1|<|b|.

Следовательно, r – r1 = 0, а поэтому и q – q1 = 0.

СОПРЯЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ.

Пусть z = a+bi, тогда:

a = Re z — действительная часть комплексного числа,

b = Im z — мнимая часть комплексного числа.

Множество точек плоскости может служить геометрическим изображением комплексных чисел.

Определение 5.Два комплексных числа равны, если равны их мнимые и действительные части (следует из геометрической интерпретации комплексных чисел).

Два комплексных числа называют сопряжёнными, если их действительные части равны, а мнимые — противоположны (сопряжённое к z обозначаем через ).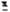

Упражнение 1.Сумма и произведение двух комплексных чисел z и 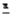(сопряжённых) — действительное число.

Теорема 2.

Справедливы следующие соотношения:

1) = + ;

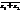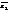2) = – ;

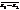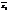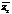3) = ;

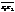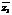
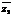4) = .

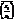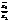Доказательство.

Доказательство 1) – 4) однообразно и сводится к подсчёту левой и правой частей и их сравнению. Например: z₁=a+bi, z₂=c+di. Докажем

1) 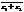= 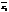+ 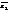. По определению

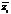= a-bi ; 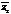=c-di и

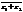= (a+c)–(bi+di),

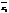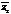+ = (a–bi)+(c–di) = (a+c)–(bi+di).

Значит = + .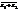

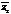КОРНИ ИЗ ЕДИНИЦЫ.

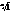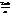1=cos0+isin0 Þ =cos +isin 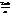, k=0,1,…,n-1.

Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей.

Теорема 1.

Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1.

Доказательство:

Возьмём a = 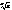= 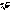(cos 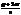+i sin 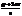), где s–фиксированное число.

e₁, e₂,…, e_n – так обозначим все корни .

Домножим каждый из корней e₁,…, e_n на a. Они разные, все являются корнями n–той степени из z, ибо (ae_i)ⁿ = z и их n штук.

Теорема доказана.

Теорема 2.

Произведение двух корней n–той степени из единицы есть корень степени n из единицы.

Следствие.

Степень корня n–той степени из единицы есть корень степени n из единицы.

Все ли корни из 1 равноправны?

n=4 ; 1, –1, i, –i — корни из единицы.

i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни.

Определение 1.

Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n.

Всегда ли есть первообразный корень?

Всегда! Например: cos 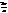+i sin .

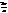Упражнение. Доказать, что корень n–той степени

e_k = cos 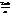+ i sin 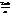будет первообразным, если n и k — взаимно простые (не имеют общих делителей отличных от 1)

ЧИСЛОВОЕ ПОЛЕ.

В множествах Q Ì R Ì C возможны четыре операции +, - , * , / .

Определение 1. Подмножество K Ì C множества комплексных чисел C, состоящее более, чем из одного элемента, называют числовым полем, если выполняются следующие условия:

1) " a, bÎK Þ a+bÎK , то есть в множестве K всегда возможно сложение;

2) " aÎK Þ –aÎK ;

3) " a, bÎK Þ abÎK , то есть задано умножение в K (K замкнуто относительно умножения);

4) " a ¹ 0 ; a(^-1)ÎK.

Из 2) с учётом 1) получаем, что в K всегда возможно вычитание.

Из 4) с учётом 3) получаем, что в K всегда возможно деление на число не равное 0.

Q — поле рациональных чисел;

R — поле вещественных чисел;

C — поле комплексных чисел.

Упражнение 1.Числовое поле всегда бесконечно.

Упражнение 2. Любое числовое поле всегда содержит Q (множество рациональных чисел).

Пример поля отличного от Q, R и C:

K = {a+b 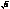, где a и b ÎQ }.

ТРАНСПОНИРОВАНИЕ МАТРИЦ.

Определение 1. Пусть A = (aij) (n x m). Транспонирование матрицы — это такое ее преобразование, при котором строка с номером i записывается в столбец с тем же номером.

Обозначение: А^t , А^tr , А'.

Пример:

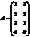, то .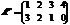

Теорема 5. Имеют место следующие равенства:

1. (А^t)^t = A.

2. (αA + βB)^t = αA^t + βB^t.

3. (AB)^t = В^tА^t .

Причем, А и В — матрицы подходящих размеров, α и β — любые числа.

< 1. А = (а_ij)_{m x n}

(A)^t = (а_ji)_{n x m} Þ (А^t)^t = A.

3. Пусть имеем А = (а_ij)_{m x n} и B = (b_ij)_{n x s} . Тогда A(^t) = ( ij) (m x n) , B (^t)=( ij) (s x m), AB = (cij) (m x s), (BА)(^t) = (dij)(s x m)

Матрица В(^t)A(^t) и AB)(^t)одинаковых размеров, и чтобы доказать, что В(^t)A(^t) = (AB)(^t), надо показать, что на одинаковых местах стоят одинаковые элементы.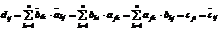

Мы получили, что на позиции ij у матрицы В(^t)A(^t) и матрицы AB)(^t) стоит один и тот же элемент. >

Определение 2. Матрица А называется симметрической, если A(^t) = А, и кососимметрической, если A(^t) = -А.

Пример. Симметрическая матрица: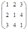

кососимметрическая матрица: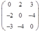

ПЕРЕСТАНОВКИ.

Пусть X — непустое множество элементов произвольной природы, так как природа элементов для нас несущественна, то в случае конечного множества считаем X ={1,2,3,…,n}

Определение 1. Любое упорядоченное расположение элементов множества X называется перестановкой множества X.

Пример:

Если X ={1,2,3,4,5} , то (2,5,3,4,1) - перестановка множества X.

Перестановку элементов множества X обозначают(a1,a2,…,an), причем среди ai (i = 1,2,…, n) нет равных.

Определение 2. Две перестановки множества X называются равными, если у них на одинаковых местах стоят одинаковые элементы.

Теорема 1.Число различных перестановок множества из n элементов равно n!

< Докажем эту теорему индукцией по числу n. При n=1 имеется одна перестановка, т.е. 1!.

Пусть n>1 и число различных перестановок, которые можно составить из заданных (n-1) элементов, равно (n-1)!. Всякая перестановка данных элементов с фиксированным первым числом а имеет вид:

a1,a2,…,an.

где a2,…,an произвольная перестановка оставшихся (n-1) элементов. По индуктивному предположению число таких перестановок равно (n-1)!. В качестве а, можно взять любой из данных n элементов, поэтому число различных перестановок заданных n элементов равно сумме n слагаемых, каждое из которых есть(n-1)!, т.е. n! >

Определение 3. Будем говорить, что в перестановке чисел (a1,a2,…,an) два числа ai,aj образуют инверсию если ai>aj, но i < j. В противном случае ai,aj образуют порядок.

Пример:

В перестановке (1 3 4 2) инверсии: 4,2 ; 3,2 , а остальные пары образуют порядок.

Определение 4. Количество пар чисел, образующих инверсию в перестановке, называют числом инверсий данной перестановки. Отображение 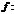X®X будем называть преобразованием множества X.

Пусть множество X состоит не менее чем из двух элементов a,bÎX.

Определение 5. Преобразование множества Х называют транспозицией элементов a и b, если 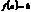, , 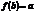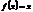" x¹a,b.Такое преобразование обозначают (a,b).

Определение 6. Перестановку называют четной, если число инверсий в ней четно, и нечетной в противном случае.

Теорема 2.Однократное применение транспозиции к перестановке изменяет ее характер четности на противоположный.

< Пусть имеется перестановка (a1,…,a,…,b,…an) (1) . Применим к ней транспозицию(a,b), получим(a1,…,b,…,a,…an) (2). Рассмотрим несколько случаев:

1. Пусть a и b стоят рядом. Если a и b в (1) образуют инверсию, то (2) образуют порядок. Поэтому характер четности изменяется на противоположный, ибо число инверсий изменяется на единицу.

2. Пусть a и b не стоят рядом (a1,…,a,…,b,…an). От (1) к (2) можно перейти следующим способом: a менять с рядом стоящим элементом дойти до b и b перегнать на место a. Всего нам придется применить S+1+S=2S+1 транспозиций соседних чисел, где S число элементов между a и b, поэтому характер четности перестановок (1) и (2) различны.>

Следствие.При n³2 число четных перестановок равно числу нечетных перестановок и равно n!/2.

< Пусть число четных перестановок равно S, нечетных — T. Если к каждой четной перестановке мы применим транспозицию двух элементов, мы превратим их в нечетные S£T, аналогично наоборот T £S Þ T=S

n!=S+T =2S

S=T=n!/2. >

Теорема 3.Пусть даны две различные перестановки одних и тех же чисел, тогда существует последовательность транспозиций переводящих первую перестановку во вторую.

< Пусть (a1,a2,…,an) (3) (b1,b2,…,bn) (4)

есть произвольные перестановки из n чисел. Если a1¹a2, то применив к перестановке (3) транспозицию (a1,b2) получим перестановку n чисел вида

(b1,l2,l3,…,ln) (5)

Если l2¹b2, то к перестановке (5) применим транспозицию (l2,b2).В результате получим перестановку (b1,b2,r3,…rn). Продолжаем этот процесс получаем требуемое.>

ПОДСТАНОВКИ.

Пусть 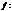X®X , при этом если — биективно, то часто называют подстановкой. Мы ограничимся случаем, когда число элементов конечно, и равно n .

X ={1,2,3,…,n}, тогда отображение можно записать в виде таблицы:

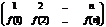(1)

Если подстановка, тогда 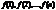— перестановка. Запись отображения 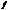в виде таблице (1) позволяет хорошо перемножать отображения.

Пример.

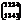
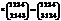
Теорема 1. Всякая подстановка конечного множества, содержащая не менее двух элементов, может быть представлена в виде произведения транспозиций.

< Пусть имеем = 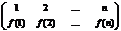.Согласно теореме 3 предыдущего параграфа, существует последовательность транспозиций переводящая первую перестановку во вторую, пусть это будет следующая последовательность транспозиций t1,t2,…,tn. Тогда очевидно, что 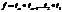, ибо отображения действуют на одном и том же множестве и результат их действия одинаков. >

Замечание. Разложение подстановки в произведение транспозиций, вообще говоря, неоднозначно.

Теорема 2. Характер четности числа сомножителей во всех разложениях подстановки в произведение транспозиций один и тот же.

◄ Пусть подстановка вида (1) разлагается в произведение k транспозиций. Это значит, что существует последовательность k транспозиций, переводящая перестановку (1,2,…,n) (2) в перестановку 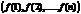(3). Однократное применение транспозиции меняет характер четности перестановки, поэтому k — четное число тогда и только тогда, когда перестановки(2) и (3) одного характера четности. Это и доказывает теорему. >

Определение 1. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетная в противном случае.

Упражнение. Число четных подстановок равно числу нечетных и равно n!/2.

ОБРАТНАЯ МАТРИЦА.

Пусть A = (aij) (n x n) квадратная матрица над полем Р.

Определение 1. Матрицу А будем называть вырожденной, если ее определитель равен 0. Матрицу А будем называть невырожденной в противном случае.

Определение 2. Пусть А Î Pn. Матрицу В Î Pn будем называть обратной к А, если АВ = ВА=Е.

Теорема (критерий обратимости матрицы).Матрица А обратима тогда и только тогда, когда она невырожденная.

< Пусть А имеет обратную матрицу. Тогда АА(^-1) = Е и, применяя теорему об умножении определителей, получаем | A | | A(^-1) | = | E | или | A | | A(^-1) | = 1. Следовательно, | A | ¹ 0.

Пусть, обратно, | A | ¹ 0. Надо показать, что существует матрица В такая, что АВ = ВА = Е. В качестве В возьмем такую матрицу:

В = ,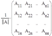

где А_ij — алгебраическое дополнение к элементу а_ij . Тогда

АВ =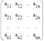

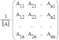
Следует заметить, что в результате получится единичная матрица (достаточно воспользоваться следствиями 1 и 2 из теоремы Лапласа), т.е. АВ = Е. Аналогично показывается, что ВА = Е. >

Пример. Для матрицы А найти обратную матрицу, или доказать, что ее нет.

А =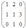

det A = -3 Þ обратная матрица существует. Теперь считаем алгебраические дополнения.

А₁₁ = -3 А₂₁ = 0 А₃₁ = 6

А₁₂ = 0 А₂₂ = 0 А₃₂=-3

А₁₃ = 1 А₂₃ = -1 А₃₃ = -1

Итак, обратная матрица имеет вид: В = =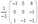

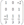
Алгоритм нахождения обратной матрицы для матрицы

1. Вычисляем det A.

2. Если он равен 0, то обратной матрицы не существует. Если det A не равен

0, считаем алгебраические дополнения .

3. Ставим алгебраические дополнения на соответствующие места.

4. Все элементы получившейся матрицы делим на det A.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Определение 1. Уравнение вида a1x1+ ....+an xn=b , где a, ... ,an — числа; x1, ... ,xn — неизвестные, называется линейным уравнением с n неизвестными.

s уравнений с n неизвестными называется системой s линейных уравнений с n неизвестными, т.е.

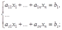(1)
Матрица А, составленная из коэффициентов при неизвестных системы (1), называется матрицей системы (1). .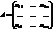

Если к матрице А добавить столбец свободных членов, то получим расширенную матрицу системы (1).

X = 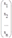— столбец неизвестных. 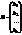— столбец свободных членов.

В матричном виде система имеет вид: AX=B (2).

Решением системы (1) называют упорядоченный набор n чисел (α1 ,…, αn) таких, что если сделаем подстановку в (1) x1 = α1, x2 = α2 ,…, xn = αn , то мы получим числовые тождества.

Определение 2. Систему (1) называют совместной, если она имеет решения, и несовместной в противном случае.

Определение 3. Две системы называют эквивалентными, если множества их решений совпадают.

Существует универсальный способ решения системы (1) — метод Гаусса (метод последовательного исключения неизвестных)

Рассмотрим более подробно случай, когда s = n. Существует метод Крамера решения таких систем.

Пусть d = det ,

dj — определитель d, в котором j–тый столбец заменен столбцом свободных членов.

ПРАВИЛО КРАМЕРА

Теорема (правило Крамера). Если определитель системы d ¹ 0, тогда система имеет единственное решение, получающееся по формулам:

x1 = d1 / d …xn = dn / d

<Идея доказательства заключается в том, чтобы переписать систему (1) в форме матричного уравнения. Положим

X = , B =

и рассмотрим уравнение AX = B (2) с неизвестной матрицей-столбцом X. Так как A, X, B — матрицы размеров n x n, n x 1, n x 1 соответственно, то произведение прямоугольных матриц АХ определено и имеет те же размеры, что и матрица В. Таким образом, уравнение (2) имеет смысл.

Связь между системой (1) и уравнением (2) заключается в том, что 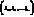является решением данной системы тогда и только тогда, когда

столбец есть решение уравнения (2).

Действительно, это утверждение означает выполнение равенства

=

= .

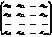
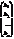
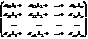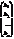Последнее равенство, как равенство матриц, равносильно системе равенств

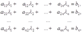
которое означает, что 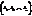— решение системы (1).

Итак, решение системы (1) сводится к решению матричного уравнения (2). Так как определитель d матрицы А отличен от нуля, она имеет обратную матрицу А^-1. Тогда АХ = В Þ А(^-1)(АХ) = А(^-1)В Þ (А(^-1)А)Х = А(^-1)В Þ ЕХ = А(^-1)В Þ Х = А(^-1)В (3). Следовательно, если уравнение (2) имеет решение, то оно задается формулой (3). С другой стороны, А(А(^-1)В) = (А А(^-1))В = ЕВ = В.

Поэтому Х = А(^-1)В есть единственное решение уравнения (2).

Так как ,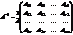

где А_ij — алгебраическое дополнение элемента a_ij в определителе d, то

= ,

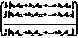откуда (4).

В равенстве (4) в скобках написано разложение по элементам j-го столбца определителя dj, который получается из определителя d после замены в нем

j-го столбца столбцом свободных членов. Поэтому, xj = dj/ d. >

Следствие. Если однородная система n линейных уравнений от n неизвестных имеет ненулевое решение, то определитель этой системы равен нулю.

23 - 24

HOД МНОГОЧЛЕНОВ.

ВЗАИМНО ПРОСТЫЕ МНОГОЧЛЕНЫ.

Определение 1. Пусть f1(x), … , fk(x)Î P[x] и Е fi(x)¹ 0 (ненулевой набор многочленов). Если $ многочлен d(x) ÎP[x] такой, что:

1) старший коэффициент d(x) равен 1.

2) d(x) / fi(x) " i=1,…,k

3) если h(x) ÎP[x] обладает свойством h(x) / fi(x) "i , то h(x) / d(x), тогда d(x) называют НОД многочленов fi,…, fk

Обозначим НОД многочленов f1,…, fk через ( f1,…, fk).

Выясним вопрос существования, однозначности и нахождения НОД.

Лемма 1: Пусть f1(x), … , fk(x)Î P[x],

М={ f1 j1+…+ fk jk | j1 ,…, j1 Î P[x] } — подмножество P[x]. f, g ÎM ; u, v ÎP[x] Þ fu+gv ÎM.

< f=f1j1+…+ fkjk g = f₁ 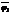+… +f_k 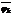fu+gv= f1(j1 u+ 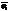v)+…+ fk(jk u+ 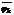v) очевидно из М. >

Теорема 1. ( О существовании НОД)

Пусть f1(x), … , fk(x)Î P[x] — некоторые многочлены, среди них есть ненулевой. Тогда многочлен наименьшей степени из М, взятый со старшим коэффициентом 1, является наибольшим общим делителем этих многочленов.

< Сразу же заметим, что в М есть ненулевой многочлен — fi(x). Докажем, что все fi(x) r=1,…,k в множестве М. По определению М

f1 j1+…+ fk jk Î М, если j1=1 ; j2=…=jk=0 ; Þf1ÎM и т.д.

Очевидно также, что в М есть многочлены со старшим коэффициентом 1 (см. Лемму1):

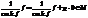
если f, g Î M.

Среди многочленов со старшим коэффициентом 1 выберем многочлен наименьшей степени. Обозначим его через d(x) и докажем, что это НОД. Во-первых, он со старшим коэффициентом 1 (мы его так выбрали).

Во-вторых, d(x) / fi(x) " i. (1)

Докажем (1). Допустим, что Ei d(x) ∤ fi(x) , т.е d(x) не делит fi(x). Разделим с остатком fi (x) на d (x): fi(x)=d(x)q(x)+r(x). Выразим r(x):

r(x)= f_i(x)+d(x)(-q(x)) Î M.

Согласно Лемме о делении с остатком ст.r < ст.d(x).

Если старший коэффициент r(x) равен 1, то сразу же имеем противоречие с выбором d, если же старший коэффициент не равен 1, сделаем, чтобы он стал равен 1:

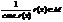(согласно Лемме 1)

Опять пришли к противоречию.

Докажем условие 3) в определении НОД.

Пусть h(x) | fi(x) " i d(x)= f1 j1+…+ fkjk ÎM Þ h(x) | d(x) (h(x) делит каждое из слагаемых, значит он делит сумму). >

Следствие (основное свойство НОД):

Наибольший общий делитель ненулевого набора многочленов f1, f2, …, fk представляется в виде: f1 y1,…,fn yk, где y1,…,ynÎP[x] .

Это следует из способа доказательства теоремы о существовании НОД, ибо НОД –элемент из М.

Теорема 2.НОД определен однозначно.

<Пусть d₁ и d₂ — наибольшие общие делители многочленов f1,…,fk.

Тогда d₁ делит f1,…,fk, то есть d₁ │ f1,…,fk, отсюда следует, что d₁ / d₂ ( по 3 свойству НОД). Аналогично d1 │ d2 ,значит можно записать d1 = a d2 . А так как d1 и d2 со старшим коэффициентом 1,то в качестве a можно взять только единицу (a=1). Значит d1=d2 ,т.е. НОД определен однозначно. >

Лемма 2.Пусть f(x)=g(x)q(x)+r(x).Тогда наибольший общий делитель f и g равен наибольшему общему делителю g и r, т.е.: ( f, g )=( g, r ).

< Доказательство теоремы следует из определения. Пусть ( f, g ) = d1 , ( g, r) = d2 .Тогда:

d1 │ f d2 │ g

Þ d1│ r Þ d1 │ d2 и d2 │ d1 Ü d2 │ f Ü

d1 │ g d2│ r

А значит: d1= d2. >

Теорема 3 (об отыскании НОД для двух многочленов).

Пусть f(x), g(x)ÎP[x], g(x)¹0. Тогда НОД многочленов f и g равен последнему, отличному от нуля, остатку в алгоритме Евклида для этих многочленов, взятому со старшим коэффициентом — единица. Если g | f, то НОД ( f, g ) равен .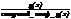

< Если g / f ,то последнее утверждение в формулировке теоремы очевидно

Применяя Лемму 2 к системе равенство (4) предыдущего параграфа, получим ,что

( f, g )=(g,r)=…=( r_k ; r_k-1 )=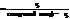

P.S. f=gq+r

g=rq₁+r₁

…………. система (4)

r_k-2=r_k-1+r_k

r_{k-1 =}r_kq_k+1+0. >

Замечание:

В теореме 3 содержится алгоритм практического отыскания НОД:

+ Ищем последний отличный от нуля остаток в алгоритме Евклида.

+ Делаем его со старшим коэффициентом единица ,это и будет НОД.

Теорема 4.(f1,……….,fk)=((f1,……..,(f)(k-1)) , fk ), k≥2.

Эта теорема указывает путь, как процесс нахождения НОД для нескольких многочленов можно свести к нахождению НОД двух многочленов.

Определение.Многочлены f_{1,……….,}f_k называются взаимно простыми, если их НОД равен единице.

Теорема 5(критерий взаимной простоты).

Многочлены (f1,………., fk ) взаимно простоты тогда и только тогда, когда $ u1,……,uk ÎP[x], такие что единица представляется в виде f1 u1 +……+fk uk.

<

Þ Имеем f1,……….,fk взаимно простые, то $ u1,……,uk ÎP[x], такие что f1u1 +……+fkuk=1. Это следует из основного свойства НОД.

Ü Пусть d(x)=( f1,……….,fk ). Значит d(x) | 1 Þ d(x)=1 и значит многочлены взаимно простые.>

26 - 27.

КОРНИ МНОГОЧЛЕНА.

Пусть f(x) — некоторый многочлен над фиксированным полем P. f(x)=an x^n+…+a0ÎP[x]. И пусть c — некоторое число (не обязательно из P). Если мы подставим вместо x число c, то получим f(c) = an c^n+…+a0 — значение многочлена при x = c. Если f(x)=g(x), то f(c)=g(c).

Определение 1.Если f(c)=0, то с называют корнеммногочлена f(x) или корнем уравнения f(х)=0.

Разделим с остатком f(x) на (x-c): f(x)=(x-c)q(x)+r(x), где r(x)=0 и r(x)=aÎ, a¹0, то есть r(x) в любом случае число.

Следующая теорема позволяет найти остаток от деления f(x) на многочлен (x-a) не выполняя самого деления.

Теорема (Безу). Остаток от деления многочлена f(x) на многочлен (x-a) равен значению этого многочлена при x=a.

Следствие. а является корнем f(x) тогда и только тогда,когда (x-а) делит f(x).

< Þ f(a)=0 (т.к. а-корень). Значит по теореме Безу (x-a) делит

f(x) Ü f(x)=(x-a)f1(x). Очевидно f(a)=0. >

Это позволяет свести нахождение всех корней многочлена к нахождению делителя первой степени. Это можно сделать при помощи схемы Горнера.

Схема Горнера:

Пусть f(x)= a0 x^n +…+an. Разделим многочлен f(x) на x-a:

f(x)=(x-a ) f 1(x)+r (1)

где

f₁ (x)=b0 x(^n-1)+…+(b) (n-1).

Сравним коэффициенты при одинаковых степенях в равенстве (1):

x^n : a0=b0

x(^n-1) : a1=b1-a b0

x(^n-2) : a2=b2-a b1

…

x^0: an = r -a (b)(n-1).

Отсюда имеем:

b0=a0

b1=a1 + a b0

b2=a2+ a b1 (2)

… …

r= an +a (b)(n-1).

Для запоминания вычисления коэффициентов применяют схему Горнера. Делают таблицу следующего вида:

	a0 a1 a2 … an
a	a0 a1+b0 c …

В первой строке этой таблицы выписывают один за другим все коэффициенты f(x), а во второе слева — элемент a. Коэффициенты частного f1(x) и остаток записывают последовательно во второй строке, согласно равенствам (2).

29 – 30.

32-34.

35-36.

ОПРЕДЕЛЕНИЕ ГРУППЫ, ВАЖНЫЕ ПРИМЕРЫ И СВОЙСТВА ГРУПП

Определение1.Пусть Г не пустое множество элементов произвольной природы. Г называется группой, если выполняются следующие условия:

1) На множестве Г задана операция °.

2) Операция ° ассоциативна.

3) Существует нейтральный элемент nÎГ.

4) Для любого элемента из Г симметричный ему элемент всегда существует и принадлежит также Г.

Пример.

Множество Z – чисел с операцией +.

Определение 2.

Группа называется абелевой, если она коммутативна относительно заданной операции °.

Важные примеры групп

1) GL(n,P) — полная линейная группа над полем P степени n. Рассмотрим множество матриц порядка n над некоторым полем P, определитель которых отличен от нуля: GL(n,P)={A Î P_n , |A|¹0}. Проверим, что это группа:

1. Операция ° задана, ибо произведение невырожденных матриц — невырожденная матрица;

2. Операция ° ассоциативна, ибо произведение матриц ассоциативно;

3. Существует нейтральный элемент — единичная матрица;

4. Обратная матрица существует и принадлежит GL(n,P), а это и есть симметричный элемент.

2) SL(n,P)={AÎP_n , |A|=1} — специальная линейная группа степени n над полем. Это множество матриц над полем P порядка n, с определителем равным 1.

1. Операция ° задана, ибо |AB| = |A||B|=1;

2. Операция ° ассоциативна;

3. Существует нейтральный элемент — единичная матрица, ибо |E|=1;

4. Существует элемент симметричный 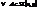— обратная матрица, так как определитель не равен нулю, и она принадлежит SL(n,P).

3) S(X) — симметричная группа на множестве X, где X — не пустое множество, S(X) — множество биективных отображений из X в X. Тождественное отображение принадлежит 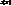, следовательно, S(X) ¹Æ

1. Операция ° задана, ибо произведение биективных отображений — биективное отображение;

2. Операция ° ассоциативна, ибо произведение отображений ассоциативно;

3. Существует нейтральный элемент e_x (тождественное отображение на X);

4. Существует обратное отображение, для любого биективного отображения и оно принадлежит S(X).

Если X — конечное множество и состоит из n элементов |C|=n, то в этом случае S(X) обозначается S_n , так как природа элементов не существенна, то полагаем Х={1,…,n}.

4) Рассмотрим множество четных подстановок A_n на множестве из n элементов. A_n ¹Æ, ибо тождественное отображение принадлежит A_n.

1. Операция ° задана (произведение четных подстановок— четная подстановка);

2. Операция ° – ассоциативна;

3. Тождественная подстановка играет роль единицы;

4. Для любой подстановки из A_n существует обратная подстановка (она тоже четная).

A_n — знакопеременная группа степени n.

Простейшие свойства групп

В группе существует единственный нейтральный элемент

В группе для каждого элемента существует единственный симметричный ему элемент

Пусть Г — группа с операцией °, тогда уравнения вида :

a°x=b и x°a=b (1) — разрешимы и имеют единственное решение.

Доказательство. Рассмотрим уравнения (1) относительно x. Очевидно, что для а $! а'. Так как операция ° — ассоциативна, то очевидно x=b°a' — единственное решение.

КОЛЬЦО. СВОЙСТВА КОЛЕЦ.

Определение.Пусть К непустое множество с двумя алгебраическими операциями: сложением и умножением. Кназывается кольцом, если выполняются следующие условия:

1)К—абелевагруппа относительно сложения;

2) умножение ассоциативно;

3)умножение дистрибутивно относительно сложения.

Если умножение коммутативно, то К называют коммутативным кольцом. Если относительно умножения есть нейтральный элемент, то К называют кольцом с единицей.

Примеры.

1) ,+,´ — коммутативное кольцо с единицей.

2) 2,+,´ — коммутативное кольцо без единицы.

3) P_n ,+, ´ — не коммутативное кольцо с единицей.

Простейшие свойства колец.

1. Так как К абелева группа относительно сложения, то на К

переносятся простейшие свойства групп.

2. Умножение дистрибутивно относительно разности:

a(b-c)=ab-ac.

Доказательство. Т.к. ab-ac+ac=ab и a(b-c)+ac=a((b-c)+c)=a(b-c+c)=ab, то

a(b-c)=ab-ac.

3. В кольце могут быть делители нуля, т.е. ab=0, но отсюда не следует,

что a=0 b=0.

Например, в кольце матриц размера 2´2, существуют элементы не

равные нулю такие, что их произведение будет нуль:

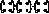,где — играет роль нулевого элемента.

4. a·0=0·а=0.

Доказательство. Пусть 0=b-b. Тогда a(b-b)=ab-ab=0. Аналогично 0·а=0.

5. a(-b)=(-a)·b=-ab.

Доказательство: a(-b)+ab=a((-b)+b)=a·0=0.

6. Если в кольце К существует единица и оно состоит более, чем из

одного элемента, то единица не равна нулю, где 1─ нейтральный

элемент при умножении; 0 ─ нейтральный элемент при сложении .

Доказательство (от противного). Предположим противное. Пусть 1=0.

Возьмем " aÎК, тогда a=a*1=a*0=0Þa=0. Значит кольцо состоит из

одного элемента. Противоречие с условием теоремы, ибо,|K|≥2.

7. Пусть К кольцо с единицей, тогда множество обратимых элементов

кольца образуют группу относительно умножения, которую называют

мультипликативной группой кольца K и обозначают K*.

Доказательство.

К^*¹Æ. Пусть aÎ K* и bÎ K*. Докажем, что abÎ K*. В самом деле

(ab)^-1=b^-1a^-1ÎK^*, ибо a^-1,b^-1ÎK^*.

ПОЛЕ. СВОЙСТВА ПОЛЯ

Определение.Коммутативное кольцо с единицей, содержащее не менее двух элементов, в котором любой отличный от нуля элемент обратим, называется полем.

Простейшие свойства поля

1. Т.к. поле — кольцо, то все свойства колец переносятся и на поле.

2. В поле нет делителей нуля ,т.е. если ab=0 ,то a=0 или b=0.

Доказательство.

Если a¹0 ,то $ a^-1 . Рассмотрим a^-1 (ab)=( a^-1 a)b=0 , а если a¹0 ,то b=0, аналогично если b¹0

3. Уравнение вида a´x=b, a¹0, b – любое, в поле имеет единственное решение x= a^-1b, или х=b/a.

Решение этого уравнения называется частным.

Примеры.

1)PÌC, P — числовое поле.

2)P={0;1};

3) P={0;1;2} .

ХАРАКТЕРИСТИКА ПОЛЯ

Не все свойства числовых полей сохраняются в случае произвольного поля. Так, складывая число 1 само с собою несколько раз, т.е. беря любое целое положительное кратное единицы, мы никогда не получим нуля. Если же мы будем брать целые кратные единицы в каком-либо конечном поле, то среди них непременно будут равные, т.к. это поле обладает лишь конечным числом различных элементов. Если все целые кратные единицы поля P являются различными элементами поля P, т.е. k°1¹m°1(здесь и далее за 1 обозначен элемент поля = единице) при k¹m, то говорят, что поле P имеет характеристику нуль(char P=0);таковы, например, все числовые поля. Если существуют такие целые k и m, что k>m, но в P имеет место равенство k°1=m°1, то (k-m) °1=0, т.е. в P существует такое положительное кратное единицы, которое оказывается равным нулю. В этом случае P называется полем положительной характеристики. Характеристикой поля в случае поля положительной характеристики называют наименьшее натуральное р, что единица сложенная р раз дает 0.

Cвойства характеристики

1) Если char P=p>0, то p — простое число.

Доказательство (от противного).

Пусть p не простое число, а составное, т.е. p=n°s, n>1,s>1 . Сложим единицу p раз: p°1=(n°1)·( s°1)=0 Þn○1=0 либо s○1=0. Ибо в поле нет делителей нуля, но n<p и s<p. Противоречие с выбором числа p.

2) a°p =0, " aÎP .

Любой элемент поля, сложенный р раз, где p — характеристика, равен нулю.

Доказательство:

a°p= 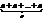=a° 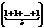= a(p°1)=a×0=0

КОНЕЧНЫЕ КОЛЬЦА И ПОЛЯ.

Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов.

Конечное поле обычно обозначается или GF(q), где q — число элементов поля.

Простейшим примером конечного поля является — кольцо вычетов по модулю простого числа p.

Характеристика конечного поля является простым числом.

§ Число элементов любого конечного поля есть его характеристика в натуральной степени: .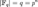

§ Для каждого простого числа p и натурального n существует конечное поле из q = pⁿ элементов, единственное с точностью до изоморфизма. Это поле изоморфно полю разложениямногочлена

Наши рекомендации