Решение системы дифференциальных уравнений методом Эйлера

Рассмотрим систему дифференциальных уравнений (ДУ) вида (17):

,

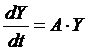где Y – вектор решений, A – матрица. В общем случае коэффициенты матрицы могут зависеть от t.

Расчетная формула по методу Эйлера для такого уравнения имеет вид:

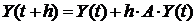(25)

Описание алгоритма решения системы ДУ методом Эйлера:

Задаем размерность системы N.

Объявляем вектор решений Y(N).

Объявляем матрицу А(N,N).

Объявляем вспомогательный вектор P(N).

Задаем начальное t₀ и конечное t_m значения отрезка интегрирования, массив начальных значений Y₀, т.е. значения системы Y(t₀) ….. Y(t_m) в точке t₀, а также количество шагов интегрирования m.

Вычисляем величину шага интегрирования h.

Цикл по t от t₀ до t_m c шагом h

Цикл по i от 1 до N

Вызвать процедуру Получить_Матрицу(А,t).

Задать P(i)=0.

Цикл по j от 1 до N.

Вычислить P(i)=P(i)+A(i,j)*Y(t).

Конец цикла по j.

Конец цикла по i.

Цикл по i от 1 до N.

Вычислить Y(i)=Y(i)+h*P(i).

Конец цикла по i.

Вызвать процедуру Печать(Y,t).

Конец цикла по t.

Алгоритм решения системы ДУ методом Эйлера на естественном языке:

N=размерность_системы

Объявить Массив Y(N),P(N),A(N,N)

t₀=0

t_m=100

m=1000

H = (t_m-t₀)/m

Получить_вектор (Y,t₀)

Цикл по t от t₀ до t_m с шагом h

Цикл по i=1 до N

Получить_матрицу (A,t)

P(i)=0

Цикл по j=1 до N

P(i) = P(i) + A(i,j)*Y(j)

Конец Цикла

Конец Цикла

Цикл по i=1 до N

Y(i) = Y(i) + h*P(i)

Конец Цикла

Печать_Вектор(Y, t)

Конец Цикла

Пример реализации алгоритма решения системы дифференциальных уравнений методом Эйлера на VFP:

SET DECIMALS TO 8

CLEAR

N=2

DIMENSION Y(N),P(N),A(N,N)

t0=0

tm=100

m=1000

H =(tm-t0)/m

Получить_вектор(@Y,N,t0)

FOR t=t0 to tm STEP h

FOR i=1 TO N

Получить_матрицу(@A,N,t)

P(i)=0

FOR j=1 TO N

P(i) = P(i) + A(i,j)*Y(j)

ENDFOR

ENDFOR

FOR i=1 TO N

Y(i) = Y(i) + h*P(i)

ENDFOR

Печать_Вектор(@Y, t)

ENDFOR

PROCEDURE Получить_вектор

PARAMETERS Y,N,t0

nf=FOPEN("U:\Prog\VFP\Euler_Sys\Y.txt",0)

FOR i=1 TO N

Y(i)=VAL(FGETS(nf))

ENDFOR

FCLOSE(nf)

ENDPROC

PROCEDURE Получить_матрицу

PARAMETERS A,N,t

nf=FOPEN("U:\Prog\VFP\Euler_Sys\A.txt",0)

FOR j=1 TO N

FOR i=1 TO N

A(i,j)=VAL(FGETS(nf))

ENDFOR

ENDFOR

FCLOSE(nf)

ENDPROC

PROCEDURE Печать_Вектор

PARAMETERS Y,t

?" t= " + ALLTRIM(STR(t))

FOR i=1 TO alen(y)

? " y(" + ALLTRIM(STR(i)) + ")= " + ALLTRIM(STR(y(i)))

ENDFOR

ENDPROC

Пример реализации алгоритма решения системы дифференциальных уравнений методом Эйлера на VBA:

Sub Euler_Sys()

n = 2

ReDim Y(n): ReDim P(n): ReDim A(n, n)

t0 = 0

tm = 100

m = 1000

h = (tm - t0) / m

Call Получить_вектор(Y(), n, t0)

For t = t0 To tm Step h

For i = 1 To n

Call Получить_матрицу(A(), n, t)

P(i) = 0

For j = 1 To n

P(i) = P(i) + A(i, j) * Y(j)

Next j

Next i

For i = 1 To n

Y(i) = Y(i) + h * P(i)

Next i

Call Печать_Вектор(Y(), t)

Next t

End Sub

Sub Получить_вектор(Y(), n, t0)

Open "U:\Prog\VFP\Euler_Sys\Y.txt" For Input As #nf

For i = 1 To n

Input #nf, Y(i)

Next i

Close #nf

End Sub

Sub Получить_матрицу(A(), n, t)

Open "U:\Prog\VFP\Euler_Sys\A.txt" For Input As #nf

For j = 1 To n

For i = 1 To n

Input #nf, A(i, j)

Next i

Next j

Close #nf

End Sub

Sub Печать_Вектор(Y(), t)

Debug.Print " t= " & CStr(t)

For i = 1 To UBound(Y)

Debug.Print " y(" & CStr(i) & ")= " & CStr(Y(i))

Next i

End Sub

Примечание. При выполнении программ на VFP и VBA значения коэффициентов матрицы А и правых частей системы задаются в текстовых файлах A.txt и Y.txt соответственно.