Лабораторная работа №7. Итерационные методы решения систем линейных уравнений. Приложения численных методов решения систем линейных уравнений

Метод Зейделя

Метод Зейделя относится к итерационным методам решения систем линейных уравнений.

Подробное описание метода Зейделя можно посмотреть в книге Самарский А.А. «Введение в численные методы». Для каждого итерационного метода решение системы линейных уравнений находится в результате многократного повторения одной и той же вычислительной процедуры, которая называется итерационной. Каждое выполнение этой процедуры называется итерацией. В каждой итерации из начального значения вектора решений X в результате выполнения итерационной процедуры получается «новое» приближенное значение вектора решений Z. Если итерационный процесс сходится, то для каждой следующей итерации разность между векторами Х и Z постоянно уменьшается и после достаточно большого количества итераций может стать меньше заданной погрешности определения вектора решений.

Если система N линейных алгебраических уравнений записана в виде:

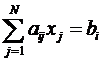, i=1, …, N (1)

где 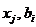– вектора неизвестных и правых частей, 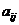– матрица коэффициентов.

Метод Зейделя применяется в одной из двух форм:

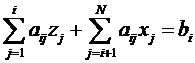, a_ij≠0, i=1, 2, …, N (2)

или

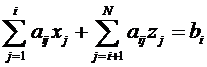, a_ij≠0, i=1, 2, …, N (3)

В расчетных формулах метода Зейделя (вариант (2), и (3)) Z – «новое» значение вектора неизвестных, а Х – начальное значение вектора Х для каждой итерации.

Рассмотрим вычислительную процедуру (2). Распишем формулу (2) для каждой строки i.

Для i=1:

,

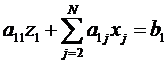Из этого уравнения легко находится первый элемент «нового» вектора решений z₁.

Для i=2

,

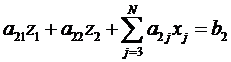из этого уравнения легко находится второй элемент «нового» вектора решений z₂,

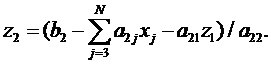
Для i=3

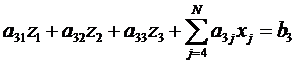, и т.д.

Для i=k

.

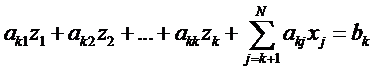Уравнение для строки с номером k можно записать в виде:

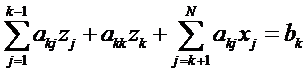, где k=1, …, N-1.

В этом уравнении первое слагаемое – 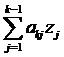состоит из известных величин матрицы коэффициентов и уже вычисленных элементов вектора решений z_j. Из него получаем значение k-й компоненты вектора решений – z_k.

Все компоненты «нового» вектора решений получаем в результате выполнения следующего алгоритма:

Цикл по k от 1 до N-1

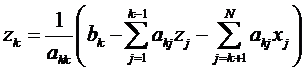
Конец Цикла

Распишем суммы в формуле в теле цикла. В результате получим более детализированный алгоритм:

Цикл по k от 1 до N

S1=0

Цикл по j от 1 до k-1

S1=S1+a_kj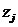

Конец Цикла

S2=0

Цикл по j от k+1 до N

S2=S2+ a_kjx_j

Конец Цикла

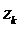=(b_k-S1-S2)/a_kk

Конец Цикла

Этот алгоритм представляет собой тело одной итерации. После получения «нового» значения вектора решений – Z, вычисляется разность векторов решений до и после итерации – d = |X-Z|. Если эта разность больше величины заданной допустимой погрешности – «новое» значение вектора решений присваивается начальному: X = Z и итерационный процесс продолжается. Начальные значение вектору X задают исходя из смысла задачи. Если d=|X-Z| меньше величины заданной допустимой погрешности – тогда итерационный процесс завершается.

Можно оптимизировать последний алгоритм, объединив циклы для вычислений S1 и S2. Поскольку в цикле для вычисления S1 компоненты 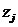получаются с предыдущей итерации, 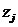можно заменить на 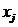, подобную же замену можно произвести в выражении 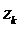=(b_k-S1-S2)/a_kk в теле основного цикла.

Цикл по k от 1 до N

S=0

Цикл по j от 1 до N

Если j≠k

S=S+a_kjx_j

Конец Если

Конец Цикла

x_k=(b_k-S)/a_kk

Конец Цикла

Теперь можно записать полный алгоритм метода Зейделя с учетом определения максимального количества итераций, требуемой погрешности и т.д.

Алгоритм решения неоднородной системы линейных уравнений методом Зейделя на естественном языке:

n=КоличествоУравнений

ОпределитьМассив a(n,n), b(n), x0(n), x(n)

Max_i = МаксимальноеЗначениеИтераций

ERR=ЗначениеПогрешности

ПолучитьКоэффициенты(@а, @b, n)

ЗадатьНачальноеЗначение(@X)

Цикл по L от 1 до Max_i

Цикл по k от l до N

x0(k)=x(k)

Конец Цикла

Цикл по k от 1 до N

S=0

Цикл по j от 1 до N

Если j≠k

S=S+a(k,j)*x(j)

Конец Если

Конец Цикла

x(k)=(b(k)-S)/a(k,k)

Конец Цикла

DX=0

Цикл по k от 1 до N

DX = DX + (x(k)-Х0(k))^2

Конец Цикла

DX = КвадратныйКорень(DX)

Если DX < ERR Тогда

ПечатьРешения (@x)

ВыходИзЦикла

Иначе

Цикл по k от l до N

x0(k)=x(k)

Конец Цикла

Конец Если

Конец Цикла

Замечание. Матрица коэффициентов в методе Зейделя не должна иметь нулевые диагональные элементы, более того, для лучшей сходимости, можно преобразовать систему уравнений к виду, когда на главной диагонали находятся максимальные по модулю элементы соответствующих подматриц.

Пример реализации алгоритма решения неоднородной системы линейных уравнений методом Зейделя на VFP:

clear

local i, j, k, l, n

local lb, ub, DX

n = 3

max_i = 100

ErrX = 0.01

lb = -0.5

ub = 0.5

dec = 4

LOCAL ARRAY a(n,n), b(n), x(n), x0(n)

? "МАТРИЦА КОЕФИЦИЕНТОВ СИСТЕМЫ А(N,N)"

CreateRNDMartix(@a, n, lb, ub, dec, 1)

? "ВЕКТОР ПРАВОЙ ЧАСТИ СИСТЕМЫ B(N)"

CreateRNDVector(@b, n, lb, ub, dec, 1)

? "НАЧАЛЬНЫЕ ЗНАЧЕНИЯ ВЕКТОРА РЕШЕНИЙ X0(N)"

CreateRNDVector(@x0, n, lb, ub, dec, 1)

For l = 1 To max_i

For k = 1 To n

x(k) = x0(k)

ENDFOR

For k = 1 To n

s = 0

For j = 1 To n

If j <> k Then

s = s + a(k, j) * x(j)

EndIf

ENDFOR

x(k) = (b(k) - s) / a(k, k)

ENDFOR

DX = 0

For k = 1 To n

DX = DX + (x(k) - x0(k)) ^ 2

ENDFOR

DX = Sqrt(DX)

? " Итерация l = " + alltrim(STR(l)) + " : DX = " + TRANSFORM(DX,"99.99999999")

If DX < ErrX Then

?

? " РЕШЕНИЕ НАЙДЕНО "

Print_Vector(@x, n, dec)

EXIT For

Else

For k = 1 To n

x0(k) = x(k)

ENDFOR

ENDIF

ENDFOR

procedure CreateRNDMartix

LPARAMETERS a, n, lb, ub, dec, prnt

For i = 1 To n

For j = 1 To n

a(i, j) = (ub - lb) * Rand() + lb

a(i, j) = Round(a(i, j), dec)

ENDFOR

ENDFOR

If prnt = 1 Then

For i = 1 To n

?

For j = 1 To n

??(a(i, j))

ENDFOR

ENDFOR

ENDIF

ENDPROC

procedure CreateRNDVector

LPARAMETERS a, n, lb, ub, dec, prnt

For i = 1 To n

a(i) = (ub - lb) * Rand() + lb

a(i) = Round(a(i), dec)

ENDFOR

If prnt = 1 Then

For i = 1 To n

? a(i)

ENDFOR

ENDIF

ENDPROC

procedure Print_Vector

PARAMETERS x, n, dec

local DStr as String

DStr = "99."

For i = 1 To dec

DStr = DStr + "9"

ENDFOR

For i = 1 To n

? " X(" + ALLTRIM(STR(i)) + ") = " + TRANSFORM(x(i), DStr)

ENDFOR

ENDPROC

Пример реализации алгоритма решения неоднородной системы линейных уравнений методом Зейделя на VBA:

Sub Zeidel_test()

Dim i, j, k, l, n

Dim lb, ub, DX

Dim a(), b(), x(), x0()

n = 3

max_i = 100

ErrX = 0.01

lb = -0.5

ub = 0.5

dec = 4

ReDim a(n, n): ReDim b(n): ReDim x(n): ReDim x0(n)

Call CreateRNDMartix(a, n, lb, ub, dec, 1)

Call CreateRNDVector(b, n, lb, ub, dec, 1)

Call CreateRNDVector(x0, n, lb, ub, dec, 1)

For l = 1 To max_i

For k = 1 To n

x(k) = x0(k)

Next k

For k = 1 To n

s = 0

For j = 1 To n

If j <> k Then

s = s + a(k, j) * x(j)

End If

Next j

x(k) = (b(k) - s) / a(k, k)

Next k

DX = 0

For k = 1 To n

DX = DX + (x(k) - x0(k)) ^ 2

Next k

DX = Sqr(DX)

Debug.Print " Итерация l = " & l & " : DX = " & DX

If DX < ErrX Then

Debug.Print

Debug.Print " РЕШЕНИЕ НАЙДЕНО "

Call Print_Vector(x(), n, dec)

Exit For

Else

For k = 1 To n

x0(k) = x(k)

Next k

End If

Next l

End Sub

Sub CreateRNDMartix(a, n, lb, ub, dec, prnt)

Dim str

For i = 1 To n

For j = 1 To n

a(i, j) = (ub - lb) * Rnd() + lb

a(i, j) = Round(a(i, j), dec)

Next j

Next i

If prnt = 1 Then

str = ""

For i = 1 To n

For j = 1 To n

str = str & a(i, j) & " : "

Next j

str = str & vbCrLf

Next i

Debug.Print str

End If

End Sub

Sub CreateRNDVector(a, n, lb, ub, dec, prnt)

For i = 1 To n

a(i) = (ub - lb) * Rnd() + lb

a(i) = Round(a(i), dec)

Next i

If prnt = 1 Then

For i = 1 To n

Debug.Print a(i)

Next i

End If

End Sub

Sub Print_Vector(x(), n, dec)

Dim i

Dim DStr, str

DStr = "0."

For i = 1 To dec

DStr = DStr + "0"

Next i

str = ""

For i = 1 To n

str = str & "X(" & i & ") = " & Format(x(i), DStr) & vbCrLf

Next i

Debug.Print str

End Sub

Результат работы программ:

МАТРИЦА КОЕФИЦИЕНТОВ СИСТЕМЫ А(N,N)

0,4194 : 0,1317 : 0,1276 :

-0,0715 : -0,402 : 0,061 :

0,1945 : 0,4137 : 0,3348 :

ВЕКТОР ПРАВОЙ ЧАСТИ СИСТЕМЫ B(N)

-0,4774

0,0434

0,4162

НАЧАЛЬНЫЕ ЗНАЧЕНИЯ ВЕКТОРА РЕШЕНИЙ X0(N)

-0,0697

0,1779

0,0025

Итерация l = 1 : DX = 2,12836329279661

Итерация l = 2 : DX = 0,658840965997187

Итерация l = 3 : DX = 8,86987750634338E-02

Итерация l = 4 : DX = 1,74853648883518E-02

Итерация l = 5 : DX = 2,35213495124003E-03

РЕШЕНИЕ НАЙДЕНО

X(1) = -1,8062

X(2) = 0,4723

X(3) = 1,7088

Замечание: данные примеры реализаций алгоритмов используют системы уравнений, коэффициенты которых сформированы случайным образом, поэтому сходимость алгоритма зависит от «удачно сформированного» вектора начальных значений.

Метод Гаусса-Зейделя

Для решения систем линейных уравнений наряду с прямыми методами решений (метод Гаусса) используются и итерационные методы. Одним из наиболее простых итерационных методов решения систем линейных уравнений является с метод Гаусса-Зейделя.

В соответствии с методом Гаусса-Зейделя исходную систему линейных уравнений

A*X=B, (4)

приводят к виду:

X=B-C*X, (5)

где матрица С=А-Е, Е–единичная матрица.

Аналогичное преобразование используется при нахождении корня нелинейного уравнения методом простой итерации.

Алгоритм метода Гаусса-Зейделя состоит в следующем: на первом этапе задается начальное приближение вектора X (либо его первая компонента), далее по формуле (5) вычисляется новое улучшенное значение X. Итерации повторяются до тех пор, пока не выполнится условие |X_n-1-X_n| < e.

Применение метода Гаусса-Зейделя приводит к решению не для всех матриц А системы (4) как и метод простой итерации. Условие сходимости метода Гаусса-Зейделя состоит в том, что каждый диагональный элемент должен быть по модулю больше либо равен сумме всех недиагональных элементов, причем хотя бы для одного элемента должно выполняться строгое неравенство.

Описание алгоритма решения системы линейных уравнений методом Гаусса-Зейделя:

Задаем точность вычислений tochn и максимальное количество итераций метода Гаусса-Зейделя max_k.

Задаем коэффициенты исходной системы линейных уравнений a(n,n) и правые части b(n).

Задаем начальные значения решений системы x₀(n).

В соответствии с методом Гаусса-Зейделя вычисляем вспомогательную матрицу c(n,n)=a(n,n)-e(n,n), где e(n,n)=0 при i<>j, и e(n,n)=1 при i=j.

Задаем равными нулю количество итераций метода – k и количество «правильно» найденных значений x(n) – corr.

Задаем условный цикл по k, с условием повторения тела цикла пока количество «правильно» найденных значений x(n) – corr меньшеколичества уравнений n.

Зануляем значений «правильно» найденных значений corr=0 на данной итерации и увеличиваем счетчик цикла k=k+1.

В соответствии с методом Гаусса-Зейделя, используя найденные ранее значения вспомогательной матрицы c(n,n), вычисляем произведение матрицы c(n,n) и x_k-1(n).

Вычисляем x_k(1…n)=b(1…n)- c(n,n)×x_k-1(n).

Подсчитываем количество «правильно» (т.е. с заданной точностью) вычисленных значений x_k(1…n).

Копируем вычисленные значения x_k(1…n) в x₀(1…n) для следующей итерации метода.

Выводим на экран значения номера итерации, количество «правильно» вычисленных x_k(1…n), а также сами значения x_k(1…n).

Задаем ветвление: если значение счетчика итераций k равно максимально допущенному количеству max_k задаем значение «правильно» вычисленных x_k(1…n) – corr равное количеству уравнений системы n.

Конец итераций по k.

Задаем ветвление: если счетчик итераций метода k достиг максимально допустимого количества, то выводим на экран «Решение не найдено за max_k итераций», иначе – вывод на экран сообщения «Решение найдено за k итераций» и вычисленные значения решений системы линейных уравнений - x_k(1…n).

Конец алгоритма.

Пример алгоритма решения системы линейных уравнений методом Гаусса-Зейделя на естественном языке:

n=размерность_системы

dec=количество_знаков_после_запятой

tochn=1/(10^dec-1)

max_k=максимальное_число_итераций

Определить Массив a(n,n),c(n,n),b(n),x0(n),x(n)

Цикл по i от 1 до n

Цикл по j от 1 до n

a(i,j)=Если(i=j,Случайный(),0.1*Случайный())

c(i,j)=0

Конец Цикла

b(i)=10*Случайный()

Конец Цикла

Вызвать Печать_Матрицы(@a,@b,n,dec)

Цикл ПО i от 1 до n

x0(i)=b(i)

Конец Цикла

Цикл по i от 1 до n

Цикл по j от 1 до n

c(i,i)=a(i,i)-Если(i=j,1,0)

Конец Цикла

Конец Цикла

k=0

corr=0

Цикл Пока corr<n

corr=0

k=k+1

Цикл по i от 1 до n

s=0

Цикл по j от 1 до n

s=s+c(i,j)*x0(j)

Конец Цикла

x(i)=b(i)-s

Конец Цикла

Цикл по i от 1 до n

Если Модуль(x(i)-x0(i))<tochn Тогда

corr=corr+1

Конец Если

x0(i)=x(i)

Конец Цикла

Печать " k= "+k

Печать " correct x "+corr

Вызвать Печать_Вектор(@x,n,dec)

corr=Если(k>max_k-1,n,corr)

Конец Цикла Пока

Если k=max_k Тогда

Печать " Решения не найдены за " + max_k+ " итераций "

Иначе

Печать " Необходимая точность достигнута за " + k+ " итераций"

Печать " Решения системы найдены "

Вызвать Печать_Вектора(@x,n,dec)

Конец Если

Определить Процедуру Печать_Вектора

Параметры x,n,dec

Определить Массив x(n)

Цикл по i от 1 до n

Печать x(i)

Конец Цикла

Конец Определения Процедуры

Определить Функцию Печать_Матрицы

Параметры a,b,n,dec

Определить Массив a(n,n),b(n)

Цикл по i от 1 до n

Цикл по j от 1 до n

Печать a(i,j)

Конец Цикла

Печать " :" + b(i)

Конец Цикла

Возврат

Конец Определения Функции

Пример реализации алгоритма решения системы линейных уравнений методом Гаусса-Зейделя на VFP:

CLEAR

n=3

dec=3

tochn=1/(10^dec-1)

max_k=500

DIMENSION a(n,n),c(n,n),b(n),x0(n),x(n)

FOR i=1 TO n

FOR j=1 TO n

a(i,j)=IIF(i=j,RAND(),0.1*RAND())

c(i,j)=0

ENDFOR

b(i)=10*RAND()

ENDFOR

Print_Matrix(@a,@b,n,dec)

FOR i=1 TO n

x0(i)=b(i)

ENDFOR

FOR i=1 TO n

FOR j=1 TO n

c(i,i)=a(i,i)-IIF(i=j,1,0)

ENDFOR

ENDFOR

k=0

corr=0

DO WHILE corr<n

corr=0

k=k+1

FOR i=1 TO n

s=0

FOR j=1 TO n

s=s+c(i,j)*x0(j)

ENDFOR

x(i)=b(i)-s

ENDFOR

FOR i=1 TO n

IF ABS(x(i)-x0(i))<tochn then

corr=corr+1

ENDIF

x0(i)=x(i)

ENDFOR

?

? " k= "+STR(k,5,0)," )"

? " correct x "+STR(corr,5,0)

Print_Vector(@x,n,dec)

corr=IIF(k>max_k-1,n,corr)

ENDDO

IF k=max_k then

?

? " Решения не найдены за " + STR(max_k,dec,0)+ " итераций "

ELSE

?

? " Необходимая точность достигнута за " + STR(k,dec,0)+ " итераций "

? " Решения системы найдены "

Print_Vector(@x,n,dec)

ENDIF

PROCEDURE Print_Vector

LPARAMETERS x,n,dec

DIMENSION x(n)

?

FOR i=1 TO n

?STR(x(i),dec*2-2,dec)

ENDFOR

ENDPROC

FUNCTION Print_Matrix

LPARAMETERS a,b,n,dec

DIMENSION a(n,n),b(n)

FOR i=1 TO n

?

FOR j=1 TO n

?? STR(a(i,j),dec*2+2,dec)

ENDFOR

?? " :" + STR(b(i),dec*2+2,dec)

ENDFOR

RETURN

ENDFUNC

В данной реализации значения коэффициентов матрицы системы уравнений a(n,n) и правых частей уравнений b(n) заданы случайным образом, а начальные значения вектора решений равны вектору правой части системы x₀(n)= b(n).

Пример реализации алгоритма решения системы линейных уравнений методом Гаусса-Зейделя на VBA:

Sub Gauss_Zeidel()

Dim a(), b(), x0(), x()

n = 3

dec = 3

tochn = 1 / (10 ^ dec - 1)

max_k = 500

ReDim a(n, n): ReDim b(n): ReDim x0(n): ReDim x(n)

For i = 1 To n

For j = 1 To n

a(i, j) = IIf(i = j, Rnd(), 0.1 * Rnd())

Next j

b(i) = 10 * Rnd()

Next i

Debug.Print "КОЕФИЦИЕНТЫ СИСТЕМЫ А(N,N) И B(N)"

Call Print_Matrix(a(), b(), n, dec)

Debug.Print

For i = 1 To n

x0(i) = b(i)

Next i

For i = 1 To n

a(i, i) = a(i, i) - 1

Next i

k = 0

corr = 0

Do While corr < n

corr = 0

k = k + 1

For i = 1 To n

s = 0

For j = 1 To n

s = s + a(i, j) * x0(j)

Next j

x(i) = b(i) - s

Next i

For i = 1 To n

If Abs(x(i) - x0(i)) < tochn Then

corr = corr + 1

End If

x0(i) = x(i)

Next i

Debug.Print " Итерация k = " & k & " Найдено " & corr & " из " & n & " решений "

'Call Print_Vector(x(), n, dec)

corr = IIf(k > max_k - 1, n, corr)

Loop

If k = max_k Then

Debug.Print

Debug.Print " Решения не найдены " & max_k & " итераций "

Else

Debug.Print

Debug.Print " Необходимая точность достигнута за " & k & " итераций "

Debug.Print " Решения системы найдены "

Call Print_Vector(x(), n, dec)

End If

End Sub

Sub Print_Vector(x(), n, dec)

Dim i

Dim DStr, str

DStr = "0."

For i = 1 To dec

DStr = DStr + "0"

Next i

str = ""

For i = 1 To n

str = str & "X(" & i & ") = " & Format(x(i), DStr) & vbCrLf

Next i

Debug.Print str

End Sub

Sub Print_Matrix(a(), b(), n, dec)

Dim i

Dim DStr, str

DStr = "0."

For i = 1 To dec

DStr = DStr + "0"

Next i

str = ""

For i = 1 To n

str = str & vbCrLf

For j = 1 To n

str = str & Format(a(i, j), DStr) & " : "

Next j

str = str & " : " & Format(b(i), DStr)

Next i

Debug.Print str

End Sub

Результат работы программы на VBA:

КОЕФИЦИЕНТЫ СИСТЕМЫ А(N,N) И B(N)

0,799 : 0,096 : 0,094 : : 1,143

0,063 : 0,599 : 0,025 : : 8,602

0,044 : 0,025 : 0,379 : : 5,266

Итерация k = 1 Найдено 0 из 3 решений

Итерация k = 2 Найдено 0 из 3 решений

Итерация k = 3 Найдено 0 из 3 решений

Итерация k = 4 Найдено 0 из 3 решений

Итерация k = 5 Найдено 0 из 3 решений

Итерация k = 6 Найдено 0 из 3 решений

Итерация k = 7 Найдено 0 из 3 решений

Итерация k = 8 Найдено 0 из 3 решений

Итерация k = 9 Найдено 1 из 3 решений

Итерация k = 10 Найдено 1 из 3 решений

Итерация k = 11 Найдено 1 из 3 решений

Итерация k = 12 Найдено 1 из 3 решений

Итерация k = 13 Найдено 1 из 3 решений

Итерация k = 14 Найдено 1 из 3 решений

Итерация k = 15 Найдено 2 из 3 решений

Итерация k = 16 Найдено 2 из 3 решений

Итерация k = 17 Найдено 2 из 3 решений

Итерация k = 18 Найдено 2 из 3 решений

Итерация k = 19 Найдено 3 из 3 решений

Необходимая точность достигнута за 19 итераций

Решения системы найдены

X(1) = -1,800

X(2) = 14,013

X(3) = 13,206