Работа с иерархическими структурами данных. Операции на деревьях

Дерево-структура данных, представляющих собой ориентированный связный граф. Элементы данных, составляющие дерево, обычно называют «узлами». Для обозначения коллекции узлов (множества элементов, составляющих дерево) используют термин nodes. Для обозначения i-го элемента коллекции узлов используют ссылку вида nodes(i). Каждый элемент в такой структуре может иметь только один родительский элемент (parent node) и может иметь один или несколько дочерних элементов (child nodes). В каждом дереве имеется как минимум один особый элемент, у которого нет родительского узла. Такой элемент называется корнем дерева либо корневым узлом (root node). Каждый узел должен иметь свой уникальный ключ и реквизиты. Минимальный набор реквизитов ‑ один реквизит ‑ подпись узла, обычно используют два реквизита – подпись узла и числовое значение узла (некоторая сумма, характеризующая узловой объект).

Примеры древовидных структур:

· файловая система. Логические диски представляют собой корни, папки и файлы представляют собой узлы такого дерева. Если в папке содержатся файлы и вложенные папки, то для этой папки они являются дочерними узлами. Для этого дерева атрибутом будет являться имя папки или файла. Ключевым значением является физический адрес элемента файловой системы.

· иерархическая структура организации или предприятия. Корневым узлом будет головная организация. Дочерними узлами могут быть филиалы, отделы. В качестве ключевого значения может быть выбран ИНН, в качестве реквизитов может быть выбран доход или выручка в зависимости от поставленной задачи.

Например, структуру организации ООО «Холидей классик» можно представить в виде дерева – рис.4:

Рис. 4 Организационная структура в виде иерархической, древовидной структуры

Представим эту же структуру в виде таблицы. Каждая строка таблицы соответствует узлу. Номер элемента разместим в колонке Key, код родительского элемента – в колонке PKey, наименование узла в колонке Naimen, для хранения числовой характеристики узла добавим колонку Summa_

Key	PKey	Naimen	Summa_
1_		ООО «Холидей классик»
2_	1_	Новосибирск
3_	1_	Томск
4_	1_	Барнаул
5_	1_	Екатеринбург
6_	5_	Центральный
7_	5_	Склад4
8_	2_	Склад20
9_	2_	Склад21
10_	2_	Склад22
11_	3_	Склад5
12_	3_	Склад10
13_	6_	Склад30
14_	6_	Склад31

При использовании подобных структур в программах, можно хранить соответствующую таблицу в виде массива, текстового файла, dbf-таблицы либо таблицы какой-либо другой СУБД.

В нижеследующих примерах, для удобства, будет использовано представление в виде dbf-таблицы – derevo.dbf.

Структура dbf-таблицы:

derevo(key I, PKey , Naimen C(50), Summa_ Y).

Здесь key – уникальный ключ каждого элемента структуры, pkey – родительский ключ, naimen – наименование организации и ее структурных подразделений, Summa_ ‑ суммы соответствующих подразделений. Использование dbf-таблицы дает возможность использовать команду поиска locate for с функцией found(), команду CALCULATE FOR to с агрегатными функциями: sum(), count(), avg(), min(), max() и т.п.

Примеры процедур для работы с древовидными структурами на языкеVFP.

Типичные задачи для работы с древовидными структурами:

· Получение количества корневых элементов.

· Получение количества дочерних узлов.

· Получение ключа корневого элемента по порядковому номеру.

· Получение ключа дочернего элемента по порядковому номеру.

· Добавление дочерних узлов.

· Получение суммы узла по ключу.

· Сумма дочерних узлов.

· Сумма дочерних узлов с заменой.

· Если у узла есть дочерние узлы, то для всех дочерних узлов сумму запомнить в новую переменную.

· Заменить значение в узле с родительским кодом на новую сумму, состоящую из суммы всех дочерних узлов.

· Если дочерних узлов нет, оставить сумму родительского узла без изменения.

· Заменять сумму в узле суммой дочерних узлов.

· Получение по ключу названия узла.

1. Получение названия по ключу.

В процедуре получения названия по ключу передадим как параметр родительский ключ в переменную lp_key.

LPARAMETERS lp_key

*Сделаем проверку открыта ли таблица, если нет, то откроем ее:

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

*Командой

SELECT derevo

*выбираем таблицу

locate FOR lp_key==ALLTRIM(key)

*если находим

IF FOUND()

*возвращаем наименование

RETURN naimen

*иначе

ELSE

*возвращаем

RETURN "нет такого узла"

ENDIF

2. Замена значения, имени узла по ключу.

CLEAR

SET DEFAULT TO "u:\tree"

IF замена_текста("38_","facultet")

?"замена сделана"

ELSE

?"замены нет"

ENDIF

IF замена_суммы("20_",20000)

?"замена сделана"

ELSE

?"замены нет"

ENDIF

*добавление_дочерних_узлов("20_","org0",30000)

*!* добавление_дочерних_узлов("20_","org1",50000)

*!* добавление_дочерних_узлов("20_","org2",80000)

*!* добавление_дочерних_узлов("20_","org3",50000)

? "сумма_дочерних_узлов_с_заменой для узла 16_=", сумма_дочерних_узлов_с_заменой("16_")

? "сумма_дочерних_узлов_с_заменой для узла 45_=", сумма_дочерних_узлов_с_заменой("45_")

kor=получение_количества_корневых_элементов()

?"корневых элементов=", kor

FOR i=1 TO kor

x=получение_ключа_корневого_элемента_по_порядковому_номеру(i)

?"корневой элемент номер=", i, "имеет ключ", x

? "дочерних элементов=", получение_количества_дочерних_узлов(x)

FOR k=1 TO получение_количества_дочерних_узлов(x)

? k, получение_ключа_дочернего_элемента_по_порядковому_номеру(x,k)

ENDFOR

ENDFOR

k="2_"

a=получение_названия_по_ключу(k)

s=получение_суммы_узла_по_ключу(k)

n=получение_количества_дочерних_узлов(k)

?"Для ключа=",k," Наименование=",a, " сумма=", s, n

k="17_"

a=получение_названия_по_ключу(k)

s=получение_суммы_узла_по_ключу(k)

n=получение_количества_дочерних_узлов(k)

?"Для ключа=",k," Наименование=",a, " сумма=", s, n

k="31_"

a=получение_названия_по_ключу(k)

s=получение_суммы_узла_по_ключу(k)

n=получение_количества_дочерних_узлов(k)

?"Для ключа=",k," Наименование=",a, " сумма=", s, n

?"сумма_дочерних_узлов=", сумма_дочерних_узлов("16_")

PROCEDURE получение_названия_по_ключу

LPARAMETERS lp_key

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

locate FOR lp_key==ALLTRIM(key)

IF FOUND()

RETURN naimen

ELSE

RETURN "нет такого узла"

ENDIF

PROCEDURE получение_суммы_узла_по_ключу

LPARAMETERS lp_key

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

locate FOR lp_key==ALLTRIM(key)

IF FOUND()

RETURN summa_

ELSE

RETURN 0

ENDIF

PROCEDURE получение_количества_дочерних_узлов

LPARAMETERS lp_key

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

COUNT FOR lp_key==ALLTRIM(pkey) TO b

RETURN b

PROCEDURE получение_количества_корневых_элементов

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

COUNT FOR LEN(ALLTRIM(pkey))=0 TO g

RETURN g

PROCEDURE получение_ключа_корневого_элемента_по_порядковому_номеру

LPARAMETERS n

LOCAL i

* порядковый номер корневого элемента

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

i=0

SELECT derevo

SCAN

IF LEN(ALLTRIM(pkey))=0

i=i+1

IF i=n

RETURN ALLTRIM(key)

ENDIF

ENDIF

ENDSCAN

return "не найдено"

PROCEDURE получение_ключа_дочернего_элемента_по_порядковому_номеру

LPARAMETERS bas_key,n

LOCAL i

* bas_key-ключ базового элемента, n-порядковый номер корневого элемента

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

i=0

SELECT derevo

SCAN

IF ALLTRIM(pkey)=bas_key

i=i+1

IF i=n

RETURN ALLTRIM(key)

ENDIF

ENDIF

ENDSCAN

return "не найдено"

PROCEDURE замена_текста

LPARAMETERS key_, naimen_

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

LOCATE FOR key_=ALLTRIM(key)

IF FOUND()

replace naimen WITH naimen_

RETURN .t.

ELSE

return .f.

ENDIF

PROCEDURE замена_суммы

LPARAMETERS key_, sum_

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

LOCATE FOR key_=ALLTRIM(key)

IF FOUND()

replace summa_ WITH sum_

RETURN .t.

ELSE

return .f.

ENDIF

PROCEDURE добавление_дочерних_узлов

lparameters bas_key, naimen_, sum_

LOCAL s

SET TALK OFF

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

LOCATE FOR bas_key=ALLTRIM(pkey)

IF FOUND()

CALCULATE MAX(VAL(key) ) TO s

APPEND BLANK

replace naimen WITH naimen_;

, key WITH ALLTRIM(STR(s+1))+"_";

, pkey WITH bas_key;

, summa_ with sum_

RETURN .t.

ELSE

RETURN .f.

ENDIF

PROCEDURE сумма_дочерних_узлов

lparameters bas_key

LOCAL s

SET TALK OFF

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

s=0

CALCULATE suM(summa_) FOR bas_key==ALLTRIM(pkey) to s

RETURN s

PROCEDURE сумма_дочерних_узлов_с_заменой

lparameters bas_key

LOCAL s

SET TALK OFF

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

*проверка на наличие дочерних узлов

IF получение_количества_дочерних_узлов(bas_key)=0

RETURN .f.

ENDIF

s=0

CALCULATE suM(summa_) FOR bas_key==ALLTRIM(pkey) to s

LOCATE FOR bas_key==ALLTRIM(key)

IF FOUND()

replace summa_ with s

RETURN .t.

ELSE

RETURN .f.

ENDIF

* заменять сумму в узле суммой дочерних узлов

CLEAR

SET DEFAULT TO "u:\tree"

замена_итог_суммы("50_")

PROCEDURE замена_итог_суммы

LPARAMETERS p,s

LOCAL s, k, x

*p-ключ родительского элемента

? "вызов замена_итог_суммы ",p

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

s=0

IF получение_количества_дочерних_узлов(p)=0

? " узел ",p

s=получение_суммы_узла_по_ключу(p)

? s

ELSE

? "Просмотр всех дочерних узлов узла с кодом=",p

SCAN FOR ALLTRIM(pkey)==p

x=ALLTRIM(key)

k=RECNO()

? " pkey=",p," x=key= ",x

s=s+замена_итог_суммы(x)

?? "s=",s

GO k

ENDSCAN

LOCATE FOR p==ALLTRIM(key)

IF FOUND()

replace summa_ WITH s

ENDIF

ENDIF

RETURN s

PROCEDURE получение_количества_дочерних_узлов

LPARAMETERS lp_key

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

COUNT FOR lp_key==ALLTRIM(pkey) TO b

RETURN b

PROCEDURE сумма_дочерних_узлов_с_заменой

lparameters bas_key

LOCAL s

SET TALK OFF

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

*проверка на наличие дочерних узлов

IF получение_количества_дочерних_узлов(bas_key)=0

RETURN .f.

ENDIF

s=0

CALCULATE suM(summa_) FOR bas_key==ALLTRIM(pkey) to s

LOCATE FOR bas_key==ALLTRIM(key)

IF FOUND()

replace summa_ with s

RETURN .t.

ELSE

RETURN .f.

ENDIF

PROCEDURE получение_суммы_узла_по_ключу

LPARAMETERS lp_key

IF NOT USED("derevo")

USE derevo IN 0

ENDIF

SELECT derevo

locate FOR lp_key==ALLTRIM(key)

IF FOUND()

RETURN summa_

ELSE

RETURN 0

ENDIF

Контрольные вопросы

1. Дать понятие рекурсии.

2. Дать определение рекурсивного алгоритма.

3. Привести примеры рекурсивных алгоритмов.

4. Что такое “Точка останова” рекурсивной процедуры?

5. Дать определение графа.

6. Дать определение иерархической структуры.

7. Дать определение родительского, дочернего элемента, листа, ветки, корня.

8. Какие операции можно проводить на иерархических структурах?

9. Как представить иерархическую структуру в табличном виде?

10. Привести алгоритм добавления дочернего элемента.

11. Привести алгоритм поиска дочернего элемента по его ключу.

12. Привести алгоритм получения количества дочерних элементов.

13. Привести алгоритм получения суммы значений числовых атрибутов дочерних элементов данного узла.

14. Привести алгоритм получения среднего значения числовых атрибутов дочерних элементов данного узла.

15. Привести алгоритм получения максимального или минимального значения числовых атрибутов дочерних элементов данного узла.

16. Как осуществляется поиск в иерархической структуре?

17. Приведите алгоритм вывода на экран иерархической структуры.

Задания

Задание 1. Написать программу построения изображения, представленного на рисунке 5.

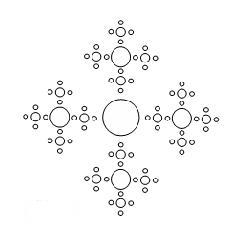
Рис.5

Рекомендации: На рисунке бóльшая окружность окружена четырьмя окружностями поменьше, каждая из которых в свою очередь окружена четырьмя окружностями с еще меньшим радиусом. Всего изображено четыре уровня окружностей.

Для того, чтобы составить программу построения этого изображения, можно:

§ описать процедуру изображения одной окружности с четырьмя окружностями поменьше;

§ для изображения каждой окружности следующего уровня использовать эту же процедуру, только с другими значениями параметров (координат центров, величин радиусов и т. д.).

Алгоритм рисования окружности радиуса r с центром в точке (x,y) с четырьмя окружностями вокруг (при этом необходимо знать расстояния r1от точки (x,y)до центров окружностей окружения, которые равны): пусть 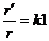, где 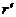- радиус окружности окружения, .

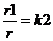Таким образом, в описанной процедуре осуществляется вызов ее же самой в качестве вспомогательной.

Для вычисления значений x1 и y1воспользуемся определениями тригонометрических функций sin и cos:

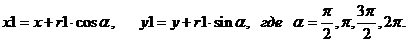
Для того, чтобы программа с данной рекурсивной процедурой работала не бесконечно, необходимо в качестве аргумента процедуры ввести некоторую величину n (здесь логично за величину n взять число уровней окружностей), которая при каждом новом вызове процедуры будет уменьшаться на 1, а в тело процедуры включить условие, что его операторы будут выполняться только при n>0. Данное условие будет играть роль «точки останова» (граничное условие), ограничивающее число вызовов процедуры.

В основной программе запрашивается количество уровней n, задаются координаты центра большой окружности (x,y) и ее радиус r, а также коэффициенты k1и k2. Центр самой большой окружности располагается в центре экрана. Для того, чтобы проследить последовательность рисования окружностей при рекурсивных вызовах, в тело процедуры можно включить процедуру паузы.

Фрактальные кривые.

Понятие фрактала. Многие объекты обладают свойством “самоподобия”. Например, строение гористой поверхности или изрезанность морского берега, снежинка.

Математическоеописание бесконечнодробимых объектов уравнениями линий или поверхностей очень громоздко из-за большого количества мельчайших объектов. Для преодоления этой трудности математиком Исследовательского центра корпорации IBM Бенуа Мандельбротом в 1975 году был введен термин “фрактал” (от латинского fractus – раздробленный, разбитый, состоящий из фрагментов), а в 1982 году опубликована основополагающая книга “Фрактальная геометрия природы”, где описаны фрактальные множества, их свойства, методы получения и изображения.

В машинной графике фракталы применяются при генерации искусственных облаков, гор, поверхности моря. Образы фракталов похожи на природные объекты — деревья, растения, узоры, звездные скопления т.п.

Задание 2. Напишите программу построения изображения, представленного на рисунке 6.

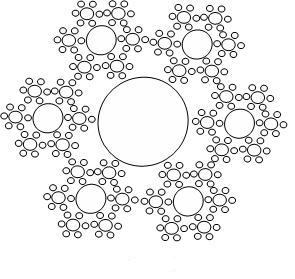
Рис.6

Задание 3. Напишите программу построения изображения, представленного на рисунке 7.

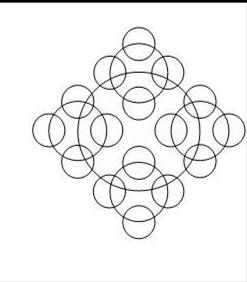
Рис. 7

Задание 4. Напишите программу построения изображения, представленного на рисунке 8 - (кривая Коха).

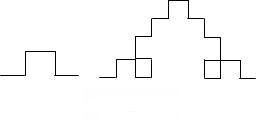
Рис. 8

Рекомендации: Процесс формирования кривой Коха состоит в следующем: отрезок разбивается на три равные части, и на средней части отрезка строится, например, квадрат или равносторонний треугольник. Для простоты рассмотрим кривую Коха с квадратом. На рисунке изображены кривые Коха первого и второго порядка. Для рисования кривой Коха используются только повороты на +90^° и -90^° и смещения вдоль прямолинейных отрезков.

Алгоритм рисования кривой Коха можно записать следующим образом:

· нарисовать прямолинейный отрезок заданной длины;

· повернуть на +90^°;

· нарисовать прямолинейный отрезок заданной длины;

· повернуть на -90^°;

· нарисовать прямолинейный отрезок заданной длины;

· повернуть на -90^°;

· нарисовать прямолинейный отрезок заданной длины.

Затем эта последовательность вновь применяется к каждому прямолинейному участку построенной ломаной линии.

Прямолинейные отрезки, начинающиеся из текущей точки и оканчивающиеся в точке с заданными координатами, в программе необходимо рисовать процедурой. Процедура рисованияявляется рекурсивной, она строит кривую Коха. Параметрами этой процедуры являются x и y (эти два числа задают единичный вектор в направлении очередного смещения) и величина смещения.

Задание 5. Напишите программу построения изображения, представленного на рисунке 8 – (“Множество Кантора”).

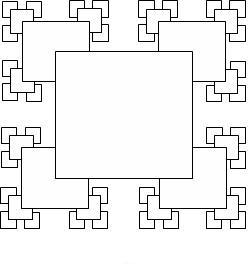
Рис. 8 Множества Кантора

Рекомендации: Данный рисунок образован квадратами. Каждый следующий квадрат в четыре раза меньше предыдущего. Центр каждого следующего квадрата расположен в вершине предыдущего квадрата и т.д. Так как рисунок состоит из однотипных элементов, и есть явная зависимость, как размеров, так и положения, следовательно, при создании данного рисунка можно использовать в программе рекурсию.

Алгоритм рисования “множества Кантора”:

· построить большой квадрат, внутреннюю часть которого, например, закрасить каким-либо цветом;

· на его вершинах, как на центрах, рисуются квадраты в четыре раза меньшие первоначального;

· это повторяется для каждого оставшегося квадрата, причем бoльшие квадраты перекрывают меньшие.

Данный алгоритм даёт возможность изменения количества уровней (глубину рекурсии), а также размеры квадратов.

Задание 6. Напишите программу построения изображения, представленного на рисунке 9 - (треугольник Серпинского).

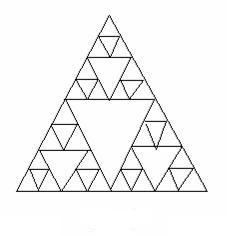
Рис. 9 Треугольник Серпинского

Рекомендации: фигура строится путем разбиения треугольника, необязательно равностороннего – средними линиями на четыре подобных треугольника, исключением центрального и рекурсивного разбиения угловых треугольников до получения площадных элементов желаемого разрешения.

Алгоритм построения треугольника Серпинского:

· строится большой внешний треугольник (А);

· строится треугольник, получающийся при соединении середин сторон большого треугольника (Б);

· строятся треугольники, получающиеся аналогично элементу Б, но в качестве большого треугольника берутся треугольники, образованные элементами А и Б.

Изображение состоит из однотипных элементов, связанных между собой зависимостью каждого следующего элемента от координат предыдущего.

Преимущество использования рекурсии –рекурсия позволяет увеличивать количество уровней, не ограничиваясь минимальными размерами самого нижнего уровня. Например, с помощью этого алгоритма можно увеличить количество уровней до пятнадцати, при этом будет ощутима только некоторая задержка при выводе изображения на экран, а без рекурсии такой рисунок построить будет практически невозможно, так как изображение будет состоять более чем из тридцати одной тысячи треугольников.

Спирали – это геометрические фигуры, у которых каждая последующая сторона немного больше предыдущей. Спираль также является примером графической рекурсии.

Задание 7.Напишите программу построения изображения, представленного на рисунке 10.

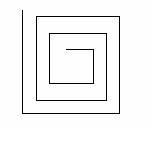
Рис. 10

Рекомендации: В изображении можно заметить ряд закономерностей:

· построение начинается из “середины” рисунка;

· каждый следующий отрезок увеличивается на определённую величину;

· все отрезки либо вертикальные, либо горизонтальные;

· при рисовании происходит последовательное построение сходных элементов с изменяющимися параметрами, следовательно, данный рисунок можно построить с использованием рекурсии.

Задание 8.Напишите программу построения изображения, в которой, кроме стороны, задан еще и угол витков спирали. На рисунке 10 приведена спираль с углом 90 градусов.

Задание 9. Напишите программу построения изображения, представленного на рисунке (“Снежинка”). Количество звеньев и ветвей, коэффициент уменьшения каждого звена ветви задаются пользователем.

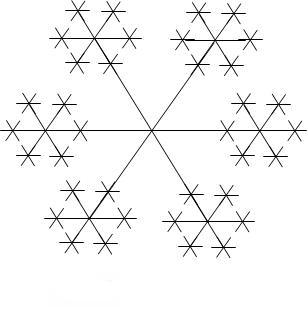
Рис. 11

Рекомендации: На рисунке 11 изображена снежинка, состоящая из 3 звеньев и 6 ветвей.

Алгоритм:

· Определить данные, необходимые для рисования снежинки и ввести обозначения: n – количество звеньев снежинки, p – количество ветвей снежинки, l – длину (в точках) ветви внутреннего звена, t – коэффициент уменьшения каждого звена.

· Центр снежинки расположить в центре экрана монитора (320, 240).

· Начинаем рисовать из центра снежинки: рисуем первый (длины l) отрезок, далее, если это не последнее звено, то рисуем отрезок длины l*t следующего звена, и так до тех пор, пока не нарисуем отрезок последнего звена (l*t^n-1).

· На последнем звене дорисовываем самую маленькую снежинку.

· Возвращаемся на предпоследний отрезок и дорисовываем самое маленькое звено со снежинкой.

· Продолжаем до тех пор, пока не нарисуем всю снежинку.

Задание 10. Напишите программу построения изображения, представленного на рисунке (“Ветка”). Длина первоначального звена, коэффициент уменьшения следующих звеньев задаются пользователем.

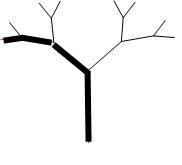
Рис. 12

Алгоритм:

· Введем обозначения: n – количество звеньев ветки, длина первоначального (вертикального) отрезка ветки (в точках) - dl, коэффициент уменьшения каждого звена – t.

· Начинаем рисовать с первоначального (вертикального) отрезка, далее, если это не последнее звено, просчитывается длина следующего отрезка и строится этот отрезок; так продолжается до тех пор, пока не прорисуются все n звеньев (часть рисунка, выделенная жирной линией).

· Далее аналогично рисованию снежинки – прорисовывается левая часть ветви, а затем правая.

При работе с данной программой обратите внимание на ограничения, накладываемые на ввод данных: n – количество звеньев (>1); dl – длина первоначального отрезка в точках, брать 10 точек …(начните со 100); 0<m<1.

Задание 11. Напишите программу построения изображения, представленного на рисунке 13 с использованием рекурсии и без нее. Укажите достоинства и недостатки каждой из программ.

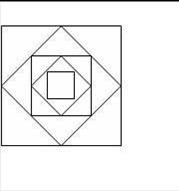
Рис. 13

Задание 12. Напишите программу построения изображения, представленного на рисунке 14 с использованием рекурсии и без нее. Укажите достоинства и недостатки каждой из программ.

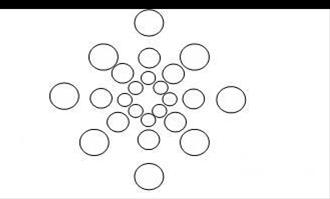
Рис. 14