Определение корня одномерного уравнения методами касательных и секущих

Для определения корней одномерных уравнений наряду с методами табуляции, дихотомии широко используются методы секущих, касательных. Методы касательных и секущих основаны на одних и тех же принципах, но метод касательных можно использовать только в случае, когда удается аналитически рассчитать производную функции.

Рассмотрим метод касательных.

Для любой функции f(x) в окрестности точки 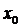справедливо разложение в ряд:

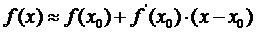. (1)

Правая часть уравнения (1) представляет собой уравнение прямой, касательной к функции f(x) в точке 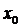(см. рис. 1):

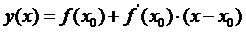. (2)

Корень уравнения (2) – 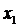соответствует точке пересечения линии касательной к функции f(x) и оси OX, эту точку в первом приближении можно считать равным корню функции f(x).

,

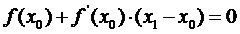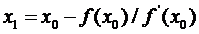(3)

Если построить касательную прямую к функции f(x) в точке 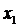, тогда точка пересечения этой касательной и оси OX будет вторым приближением к корню функции f(x). Таким образом, приближенное значение корня функции на шаге n определяется через предыдущее приближенное значение шага n-1 по формуле:

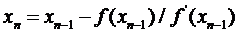(4)

Формула (4) является расчетной формулой метода касательных.

Из формулы (4) вытекает, что значение производной функции f(x) на всем интервале поиска корня не должно быть равным нулю, соответственно функция f(x) в окрестности корня должна быть монотонна.

Рассмотрим условие завершения итерационного процесса метода касательных. Если итерационный процесс сходится, то одним из определяющих условий достижения корня является условие на значение функции в точке :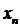

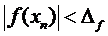, (5)

где 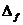- погрешность определения корня функции по величине функции.

С другой стороны, наряду с проверкой абсолютного значения функции, при выполнении итерационной процедуры метода касательных необходимо проверять условие локализации значения корня функции:

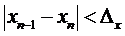, (6)

где 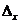- погрешность определения положения корня по оси OX.

Одновременное выполнение условий (5) и (6) может быть использовано в качестве критерия остановки итерационного процесса метода касательных.

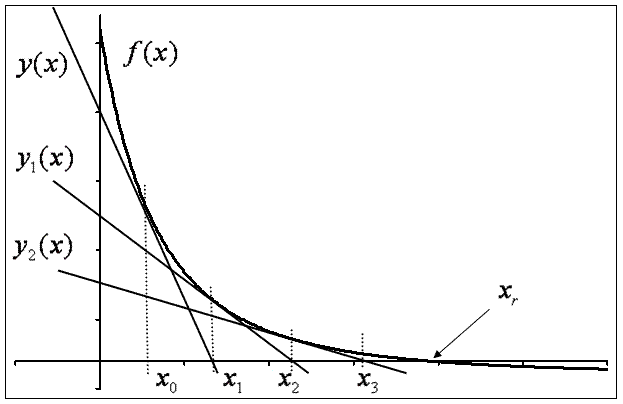
Рис.1 Иллюстрация итераций метода касательных

Метод касательных предполагает вычисление производной функции на каждом шаге. Приближенное значение производной можно получить по разностным формулам: 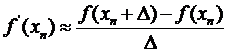- разностная производная «вперед», 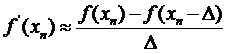- разностная производная «назад» или 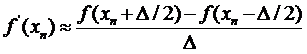- «центральная» разностная производная. В любом случае на каждом шаге необходимо два вычисления значения функции, что замедляет вычисления в случае сложной функции.

Метод секущих является модификацией метода касательных позволяющей значительно ускорить процесс вычислений.

Основное отличие метода секущих от метода касательных состоит в том, что в процессе вывода расчетной формулы вместо точного вида производной функции f(x), используется разностное представление производной:

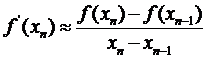. (7)

Более того, формула (7) представляет собой значение тангенса угла наклона 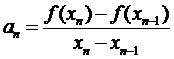(8)

прямой линии проходящей через точк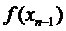и и 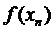- линии секущей приближения n:

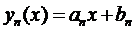. (9)

Значение коэффициента 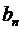уравнения (9) легко получить из условия 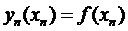или :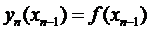

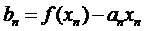
или

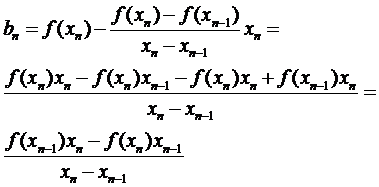
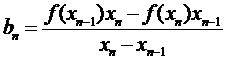(10)

В качестве приближенного значения корня метода касательных принимается точка пересечения касательной (9) оси OX: 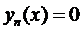, тогда приближенное значение корня 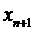получим из условия равенства нулю (9): .

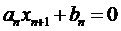Таким образом, расчетная формула для получения значения корня n приближения в соответствии с методом секущих имеет вид:

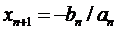, (11)

где значения коэффициентов 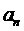и 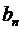определяются из (8) и (10).

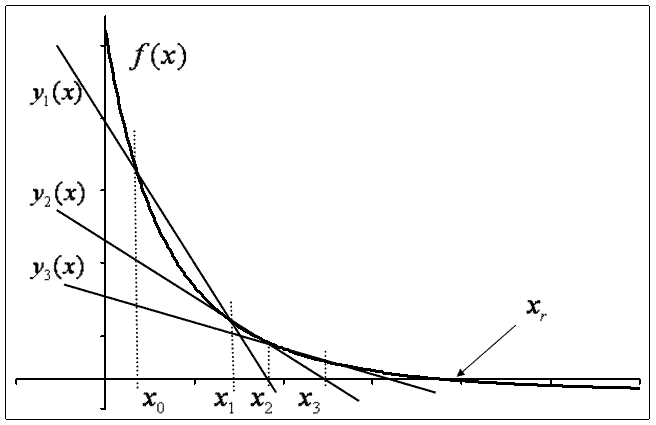
Рис.2 Иллюстрация итераций метода секущих

Критерии достижения необходимой точности определения корня методом секущих можно получить аналогично методу касательных. То есть наряду с условием на достаточно малое абсолютное значение функции в корне:

| f(x)|< e_y , (12)

(e_y – малое, близкое к нулю число), необходимо использовать условие на локализацию корня:

|x_n+1–x_n| < e_x, (13)

(e_x – малое, близкое к нулю число).

Описание алгоритма нахождения корня одномерного уравнения методом секущих:

Задаем начальные параметры алгоритма: точности нахождения корня по х и у – е_x и e_y, а также максимальное количество итераций – max_i.

Задаем начальное приближение к корню х₀ и приращение d для вычисления двух начальных точек: x₀ и x₁.

Вычисляем значения функции в точке x₀: f₀ =f(x₀)

Вычисляем значения функции в точке x₁: f₁ = f(x₁).

Цикл по i от 1 до max_i.

По формулам (8) и (10) вычисляем коэффициенты a и b уравнения скущей.

Находим приближенное значение корня x₂ по формуле (11).

Вычисляем значения функции в этой точке f₂ =f(x₂).

Вычисление погрешностей нахождения корня.

Проверяем условия достаточной малости погрешностей абсолютного значения корня функции (12) и локализации корня (13). В случае удовлетворения условия достижения корня – выход из цикла и печать результатов.

В случае неудовлетворения условия – переопределение точек для построения секущей: x₀=x₁ и x₁= x₂, а также значений функции в этих точках: f₀ = f₁, f₁ = f₂ .

Конец цикла.

Итерации продолжаются до тех пор, пока не будет удовлетворены условия достижения необходимой точности вычислений, либо количество итерации превысит значение max_i. В методе секущих на каждой итерации функция вычисляется только один раз.

Описание алгоритма нахождения корня уравнения методом секущих на естественном языке:

eps1=точность_по_оси_Х

eps2=точность_по_оси_Y

maxi=максимальное_количество_итераций

x0=начальное_приближение_к_корню

d =начальный_шаг_приращения

xn=x0+d

f0=f(x0)

fn=f(xn)

Цикл по i от 1 до maxi

x=xn-(xn-x0)*fn/(fn-f0)

fx=f(x)

err2=Модуль(xn-x)

err1=Модуль(fn-fx)

Печать i, x,fx

Если err1<eps1 AND err2<eps2 Тогда

Печать "Решение найдено: ", x

Возврат

Конец Если

x0=xn

xn=x

f0=fn

fn=fx

Конец Цикла

Определение Функции f

Параметры x

Вернуть (x-4)*(x-2)

Конец Определения Функции

Пример реализации алгоритма решения на языке VFP:

clear

eps1=0.001

eps2=0.001

maxi=1000

input "Введите начальное приближение к корню х0 :" to x0

Input "Введите начальный шаг приращения d :" to d

xn=x0+d

f0=f(x0)

fn=f(xn)

FOR i = 1 TO maxi

x=xn-(xn-x0)*fn/(fn-f0)

fx=f(x)

err2=abs(xn-x)

err1=aBS(fn-fx)

? "Итерация= "+ALLTRIM(STR(i))

?? " : x= "+ TRANSFORM(x,"99.999 999 999")

?? " : f(x)= "+ transform(fx,"99.999 999 999")

IF err1<eps1 AND err2<eps2

? "Решение найдено: ", x

RETURN

ENDIF

x0=xn

xn=x

f0=fn

fn=fx

ENDFOR

function f

LPARAMETERS x

return (x-4)*(x-2)

ENDPROC

Пример реализации алгоритма решения задачи на VBA:

Sub root2()

eps1 = 0.001

eps2 = 0.001

maxi = 1000

x0 = Val(InputBox("Введите начальное приближение к корню х0:"))

d = Val(InputBox("Введите начальный шаг приращения d:"))

xn = x0 + d

f0 = f(x0)

fn = f(xn)

For i = 1 To maxi

x = xn - (xn - x0) * fn / (fn - f0)

fx = f(x)

err2 = Abs(xn - x)

err1 = Abs(fn - fx)

Debug.Print "Итерация= " + CStr(i)

Debug.Print "x= " + Format(x, "00.000 000 000")

Debug.Print "f(x)= " + Format(fx, "00.000 000 000")

If err1 < eps1 And err2 < eps2 Then

Debug.Print "Решение найдено x= " & x

Exit Sub

End If

x0 = xn

xn = x

f0 = fn

fn = fx

Next i

End Sub

Function f(x)

f = (x - 4) * (x - 2)

End Function

Результаты работы программы на VBA для отрезка а=0, b=3:

Итерация= 1

x= 02,666 666 667

f(x)= -00,888 888 889

Итерация= 2

x= 00,000 000 000

f(x)= 08,000 000 000

Итерация= 3

x= 02,400 000 000

f(x)= -00,640 000 000

Итерация= 4

x= 02,222 222 222

f(x)= -00,395 061 728

Итерация= 5

x= 01,935 483 871

f(x)= 00,133 194 589

Итерация= 6

x= 02,007 782 101

f(x)= -00,015 503 641

Итерация= 7

x= 02,000 244 111

f(x)= -00,000 488 162

Итерация= 8

x= 01,999 999 046

f(x)= 00,000 001 907

Решение найдено x= 1,99999904632523