Способ 4. Выделение полного квадрата.

Рассмотрим применение данного метода на конкретном примере.

Пример 9.Разложить на множители: .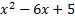

Решение:

Выделение полного квадрата обычно происходит по первым двум слагаемым. Действительно, квадрат первого – 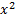– у нас уже есть. Значит, второе слагаемое должно представлять собой удвоенное произведение первого выражения на второе. То есть: 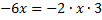. Значит, если в роли 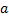из формулы квадрата разности выступает 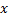, то в роли 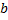должна выступать 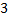. Для применения этой формулы нам не хватает 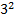. Если чего-то не хватает, то можно добавить это выражение и вычесть, чтобы не менять значение выражения. Получаем:

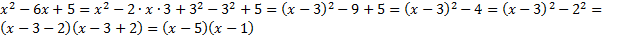
Ответ: .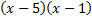

В заключение рассмотрим пример сложения дробей с применением данного метода разложения на множители.

Пример 10.Упростить: .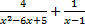

Решение:

Воспользуемся разложением на множители первого знаменателя из предыдущего примера. Получим:

.

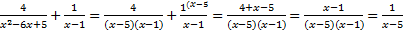При этом необходимо учесть ОДЗ данного выражения, а именно: знаменатель дроби не может равняться 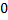. Поэтому: .

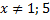Ответ: .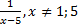

На данном уроке мы рассмотрели способы разложения знаменателя на множители при сложении и вычитании алгебраических дробей, а также применение этих способов для конкретных примеров.

Домашнее задание

1. Разложить на множители: а) 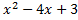, б) .

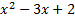2. Упростить выражение: .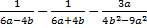

3. Построить график функции: .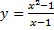

Урок 14:Задачи на сложение и вычитание дробей

На этом уроке мы продолжим рассматривать простейшие операции с алгебраическими дробями – их сложение и вычитание. Сегодня мы сделаем основной акцент на рассмотрении примеров, в которых наиболее важной частью решения будет разложение знаменателя на множители всеми способами, которые нам известны: с вынесением общего множителя, методом группировки, выделением полного квадрата, с помощью формул сокращенного умножения. В ходе урока будет рассмотрено несколько достаточно сложных задач на дроби.

1. Общий вид рассматриваемых примеров

На уроке рассмотрим и обобщим все случаи сложения и вычитания дробей: с одинаковыми и с разными знаменателями. В общем виде будем решать задачи вида:

.

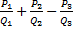Ранее мы уже видели, что при сложении или вычитании алгебраических дробей одной из важнейших операций является разложение знаменателей на множители. Аналогичная процедура проделывается и в случае обыкновенных дробей. Еще раз вспомним, каким образом необходимо работать с обыкновенными дробями.

Пример на сложение/вычитание обыкновенных дробей

Пример 1.Вычислить .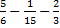

Решение.Воспользуемся, как и ранее, основной теоремой арифметики о том, что любое число можно разложить на простые множители: .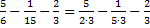

Определим наименьшее общее кратное знаменателей: 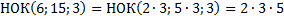– это и будет общий знаменатель дробей, и, исходя из него, определим дополнительные множители для каждой из дробей: для первой дроби 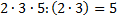, для второй дроби 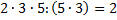, для третьей дроби .

.

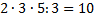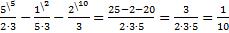Ответ. .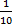

3. Методы, которые применяются для сложения/вычитания алгебраических дробей, и пример на упрощение сложного выражения

В указанном примере мы пользовались основной теоремой арифметики для разложения чисел на множители. Далее, когда в роли знаменателей будут выступать многочлены, их необходимо будет раскладывать на множители следующими известными нам методами: вынесение общего множителя, метод группировки, выделение полного квадрата, использование формул сокращенного умножения.

Пример 2. Сложить и вычесть дроби .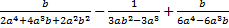

Решение.Знаменатели всех трех дробей являются сложными выражениями, которые необходимо разложить на множители, затем найти для них наименьший общий знаменатель и указать дополнительные множители для каждой из дробей. Проделаем все эти действия отдельно, а затем подставим результаты в исходное выражение.

В первом знаменателе вынесем общий множитель: 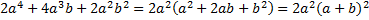– после вынесения общего множителя можно заметить, что выражение в скобках сворачивается по формуле квадрата суммы.

Во втором знаменателе вынесем общий множитель: 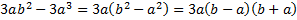– после вынесения общего множителя применяем формулу разности квадратов.

В третьем знаменателе выносим общий множитель: .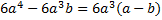

После разложения на множители третьего знаменателя можно заметить, что во втором знаменателе можно выделить множитель 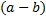для более удобного поиска наименьшего общего знаменателя дробей, сделаем мы это с помощью вынесения минуса за скобки 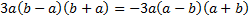, во второй скобке мы поменяли местами слагаемые для более удобной формы записи.

Определим наименьший общий знаменатель дробей как выражение, которое делится на все знаменатели одновременно, он будет равен: .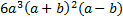

Укажем дополнительные множители: для первой дроби 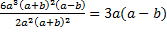, для второй дроби 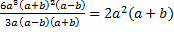– вынесенный в знаменателе минус не учитываем, т. к. запишем его ко всей дроби, для третьей дроби .

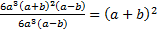Теперь выполним действия с дробями, не забыв поменять знак перед второй дробью:

.

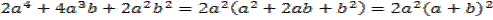На последнем этапе решения мы привели подобные слагаемые и записали их в порядке убывания степеней при переменной .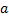

Ответ. .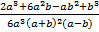

Примеры на сокращение дробей до их сложения или вычитания

На приведенном примере мы еще раз, как и на прошлых уроках, продемонстрировали алгоритм сложения/вычитания дробей, который заключается в следующем: разложить на множители знаменатели дробей, найти наименьший общий знаменатель, дополнительные множители, выполнить процедуру сложения/вычитания и, по возможности, упростить выражение и произвести сокращение. Этим алгоритмом мы будем пользоваться и в дальнейшем. Рассмотрим теперь более простые примеры.

Пример 3.Вычесть дроби .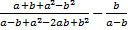

Решение. В данном примере важно увидеть возможность сократить первую дробь до приведения ее к общему знаменателю со второй дробью. Для этого числитель и знаменатель первой дроби разложим на множители.

Числитель: 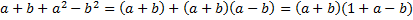– в первом действии разложили часть выражения по формуле разности квадратов, а во втором – вынесли общий множитель .

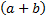Знаменатель: 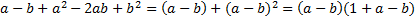– в первом действии разложили часть выражения по формуле квадрата разности, а во втором – вынесли общий множитель 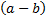. Подставим полученные числитель и знаменатель в исходное выражение и сократим первую дробь на общий множитель :

.

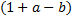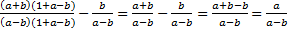Ответ: .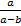

Пример 4.Выполнить действия .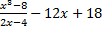

Решение.В этом примере, как и предыдущем, важно заметить и осуществить сокращение дроби до выполнения действий. Разложим числитель и знаменатель на множители.

Числитель: 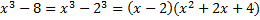– по формуле разности кубов.

Знаменатель: 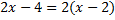– вынесли общий множитель. Подставим все в исходное выражение и сократим дробь на :

.

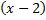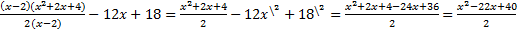После сокращения укажем область допустимых значений переменной .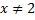

Ответ. .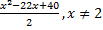

На сегодняшнем уроке мы еще раз подчеркнули важность умения раскладывать многочлены на множители при сложении и вычитании алгебраических дробей. Эта техника окажется полезной и на дальнейших уроках.

Домашнее задание

1. Выполнить действия .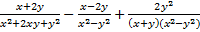

2. Выполнить действия .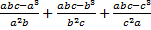

3. Выполнить действия .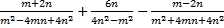

Урок 15: Контрольная работа.

1 вариант

1. При каких значениях переменной имеет смысл выражение:

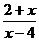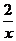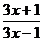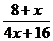а) ; ; б) ; ; в) ; .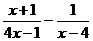

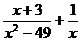2. Сократите дробь:

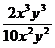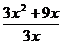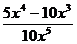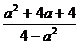а) ; ; б) ; ; в) ; .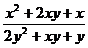

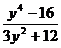3. Выполнить действия:

а) 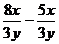; ; 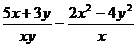б) ; ;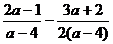

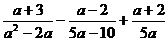в) ; .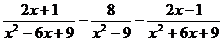

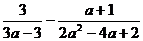4.Доказать, что значение выражения не зависит от переменной:

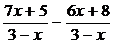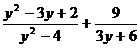а) ; б) ; в) .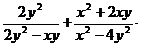

2 вариант

1. При каких значениях переменной имеет смысл выражение:

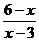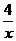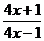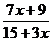а) ; ; б) ; ; в) ; .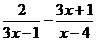

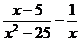2. Сократите дробь:

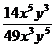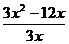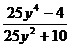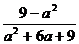а) ; ; б) ; ; в) ; .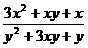

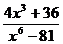3. Выполнить действия:

а) 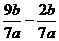; ; 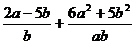б) ; ;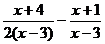

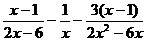в) ; .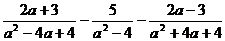

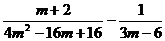4.Доказать, что значение выражения не зависит от переменной:

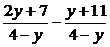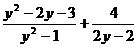а) ; б) ; в) .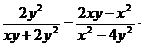

Примечание: данная контрольная работа разноуровневая, в каждом номере (№1,2,3 или 4) своего варианта нужно сделать только одно из заданий под буквой а), б) или в). Задания под буквой а) оцениваются в 1 балл; под буквой б) – 2 балла; под буквой в) – 3 балла. Каждый из вас может выбрать себе задание по силам. Удачи!