Первый и второй законы выполняются в инерциальной системе отсчета.
Третий закон справедлив в любой системе отсчёта.
Замечание 2
Первый, второй и третий законы справедливы только для свободной точки.
На первый взгляд кажется, что достаточно трех законов, чтобы описать движение точки в различных случаях.
Ничего подобного.
Во первых, когда мы записывали формулу (1), предполагалось, что на точку действует одна сила , а не несколько сил.
Во вторых, мы считали, что нет связей. Точка свободная. А на практике к точке прикладывается не одна сила, а несколько (система) и наложены ограничения – связи.
Для того чтобы в дальнейшем можно было бы решать любую задачу по динамике точке нам необходимо рассмотреть еще два закона.
Четвёртый закон (закон независимости действия сил).
Этот закон позволяет применять второй закон Ньютона к свободной материальной точке, на которую действует не одна сила, а несколько сил.
Пусть на материальную точку действует система сил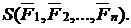 
Формулировка
Если на материальную точку действует одновременно несколько сил, то ускорение точки равно сумме тех ускорений, которые получила бы точка под действием каждой силы в отдельности,
то есть
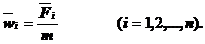(4)
где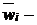 
ускорение, вызываемое силой 
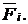,которая вызывает изменение скорости, т.е ускорение
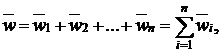(5)
Каждая сила действует в системе независимо от других, другие силы не мешают данной силе вызвать свое ускорение, и т.д. для всех остальных.
Принято говорить, чтосилы действуют независимо, от того, действует ли одна только эта сила или все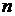 
сил одновременно.
Подставляя выражение (5) в формулу (4), получаем
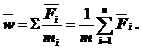
Откуда
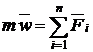
Введем обозначение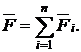 
откуда
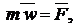
Формулировка
Из формулы (5) видно, что точка под действием системы сил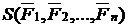 
движется так, как если бы к материальной точке была бы приложена одна сила равная сумме всех действующих сил.
В статике эта сила называлась равнодействующей.
Это означает, что в динамике, как и в статике, систему сил 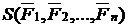, действующих на материальную точку, можно заменить равнодействующей этой системы сил.
В динамике, как и в статике, применяется закон освобождаемости от связей.
Пятый закон (закон освобождаемости от связей).
Этот закон говорит о том, что для несвободной точки связи можно отбросить, заменив их на реакции и рассматривать тело, находящееся под действием активных сил и реакций связи
Формулировка
Всякую несвободную материальную точку, находящуюся в любом движении, можно освободить от связей, заменив действия связей их реакциями, и рассматривать её как свободную, находящуюся под действием приложенных активных сил и реакций связей.
Этот закон называют также принципом освобождаемости от связей.
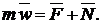(6)
Где
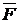- равнодействующая всех активных сил,
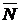равнодействующая всех реакций связей,
Формула (6) выражает основноеуравнение движения несвободной материальной точки
Дифференциальные уравнения движения материальной
Точки.
Для того, чтобы описать движение материального объекта находящегося под действием сил, необходимо составлять дифференциальные уравнения, а потом их решать.
Решение дифференциальных уравнений называется интегрированием дифференциальных уравнений.
Как известно из кинематики, движение точки математически можно описать тремя способами: векторным, координатным естественным.
Соответственно, из второго закона Ньютона следуют дифференциальные уравнения движения материальной точки ввекторной, в координатной в естественной формах.
Векторная форма
Рассмотрим свободную материальную точку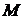 
массы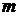 
, движущуюся под действием системы сил 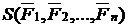относительно инерциальной системы отсчёта
Исходным уравнением является основной закон динамики :
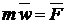. (1)
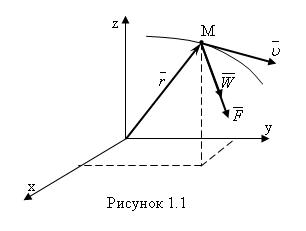
Изображаем координатную систему Оxyz – это инерциальная система отсчета, принято называть движение по отношению к инерциальной системе отсчета абсолютным движением.
Изобразим точку М и силу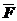 
.
Если посмотреть на первое уравнение, то чем отличается вектор силы от вектора ускорения в скалярной величине?
Скаляром массы.
Значит в этом случае сила и ускорение направлено по одной прямой.
 |
 |
Если воспользоваться формулой
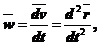
где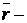 
радиус – вектор точки, то уравнение (1) принимает вид
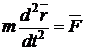(7)
Уравнение (7) называется дифференциальным уравнением движениясвободной материальной точки в векторной форме.
Для несвободной точки в правой части появится, кроме активной силы реакция.
Записываем.
Для несвободной точки уравнение (6) записывается:
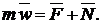
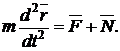(8)
Где
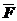- равнодействующая всех активных сил
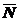- равнодействующая всех реакций связи