Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Пример:
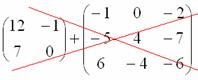
Сложить матрицы 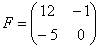и

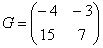
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

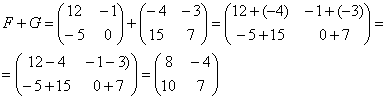
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Пример:
Найти разность матриц ,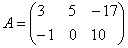

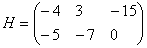
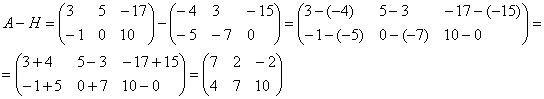
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :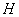

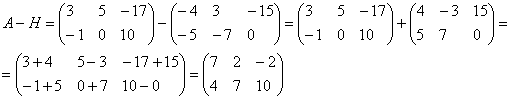
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

Чтобы матрицу 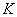можно было умножить на матрицу 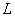необходимо, чтобы число столбцов матрицы 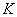равнялось числу строк матрицы .

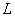Пример:
Можно ли умножить матрицу 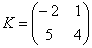на матрицу ?

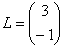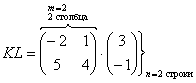
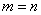, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

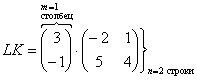
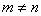, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла

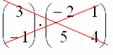
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, 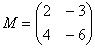и 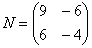возможно как умножение 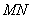, так и умножение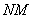

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример:
Умножить матрицу 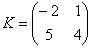на матрицу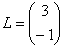
Я буду сразу приводить формулу для каждого случая:

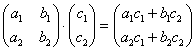– попытайтесь сразу уловить закономерность.

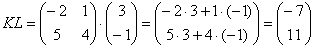
Пример сложнее:

Умножить матрицу 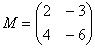на матрицу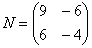

Формула: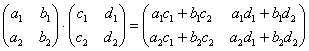

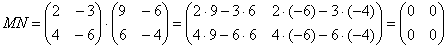
В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение 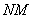(правильный ответ ).

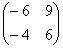Обратите внимание, что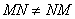 ! Это почти всегда так!

Таким образом, переставлять матрицы в произведении нельзя!

Если в задании предложено умножить матрицу 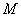на матрицу 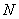, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу 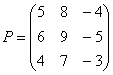на матрицу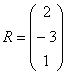

Формула очень похожа на предыдущие формулы:

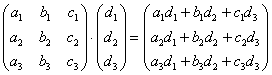
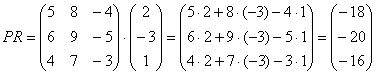
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу 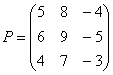на матрицу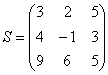

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

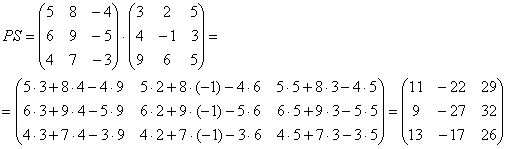
Будет время, распишу подробнее