Аксиоматический метод и его понятийный аппарат

Основные понятия. Определение. Аксиома. Аксиоматический метод. Теорема. Доказательство. Основные методы доказательств

Определение.

В любой науке, в математике тоже, существуют некоторые понятия, которые мы принимаем за исходные, или начальные понятия. Это так называемые основные понятия, определить которые достаточно сложно (именно потому, что они основные) и содержание которых можно выяснить только из опыта. Таковы, например, понятия: точки в геометрии, прямой в планиметрии, плоскости в стереометрии, материи в физике, информации в информатике.

Все остальные понятия мы объясняем, выражая их через начальные понятия. Такие объяснения называются определениями. Таким образом, каждое математическое определение опирается либо непосредственно на начальные понятия, либо на понятия, определённые прежде.

Однако здесь невозможно обеспечить всеобщего согласия. Дело в том, что одно и то же, например, геометрическое понятие можно определять различно. Диаметр окружности, например, можно определить как хорду, проходящую через центр, или как хорду наибольшей длины. Приняв за определение одно из этих свойств, можно доказать другое. Отметим, что обычно за определение берут простейшее свойство.

Аксиома. Аксиоматический метод.

При построении любой теории выделяется некоторый набор высказываний, истинность которых постулируется. Такие принимаемые без доказательства высказывания, называются аксиомами. В физике аксиомы называют постулатами, которые являются обобщением опытных данных.

Аксиомы также возникли из опыта, и опыт же проверяет истинность аксиом в их совокупности.

Аксиоматический метод – это способ построения научной (математической) теории, основу которого составляют некоторые исходные положения (аксиомы), а все остальные положения теории получаются как логические следствия аксиом.

Доказательство. Теорема.

Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством.

Высказывание, которое можно доказать, называется теоремой. Как было указано выше, опыт проверяет истинность аксиом в их совокупности. Проверка состоит в том, что все теоремы математики оказываются согласными с опытом. Этого не случилось бы, если бы система аксиом была ложной.

Каждая теорема может быть выражена в формализованной математической форме вида:

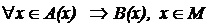
(читается: «для любого элемента х из А(х) следует В(х), где х принадлежит множеству М»).

Посылка А называется условием теоремы, а следствие В – заключением. Теорема верна, если выражающая её логическая связка, в данном случае это импликация 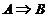(читается: «из А следует В», или «если А, то В»), обеспечивает истинное высказывание.

Рассмотрим примеры:

Теорема 1. Если сумма цифр натурального числа делится на 3, то и само число делится на 3.

Теорема 2. Если четырёхугольник является прямоугольником, то его диагонали конгруэнтны.

Теорема 3. Диагонали ромба взаимно перпендикулярны.

Из-за краткости формулировки теоремы 3 о диагоналях ромба может показаться, что эта теорема не имеет формы 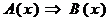. На самом деле это не так. Полная формулировка этой теоремы такова (напомним, что ромбом называется параллелограмм, у которого все стороны равны): «Для любого параллелограмма верно утверждение: если параллелограмм – ромб, то его диагонали взаимно перпендикулярны».