Кафедра математики и информатики
КАФЕДРА МАТЕМАТИКИ И ИНФОРМАТИКИ
Мелкумян Б. В., Питерцева Г. А.
ВЫСШАЯ МАТЕМАТИКА
Курс лекций
Для дистанционного обучения
студентов гуманитарных специальностей
МОСКВА 2012
Авторы – составители:
Мелкумян Б. В., Питерцева Г. А.
Высшая математика: Курс лекций.– М.: Московский университет им. С. Ю. Витте, 2012, _516_ стр.
Научный редактор:
Курс лекцийпредназначен для студентов дистанционной формы обучения гуманитарных специальностей.
Печатается по решению научно-методического совета Московского университета им. С. Ю. Витте.
© Б. В. Мелкумян, Г. А. Питерцева, 2012
© Московский университет им. С. Ю. Витте, 2012
ОГЛАВЛЕНИЕ
· Об авторах-составителях. 7
· От авторов-составителей. 7
ВВОДНАЯ ЧАСТЬ. 7
Что самое трудное в математике?. 8
Нужны ли способности?. 8
Что такое абстракция?. 8
Не затрудняет ли абстракция изучение математики?. 8
Цели и ожидаемые результаты курса. 9
Связь с другими дисциплинами. 9
План изучения курса. 10
Понятие комплексного числа. 10
График прохождения контрольных мероприятий: 11
ЛИТЕРАТУРА.. 12
Основной список. 12
Дополнительный список. 12
1. Алгебра высказываний. 12
1.1. Аксиоматический метод и его понятийный аппарат. 12
Определение. 12
Аксиома. Аксиоматический метод. 12
Доказательство. Теорема. 12
Особенность аксиоматического метода. 13
Основные методы доказательств. 13
Упражнения для самостоятельного анализа к Разделу 1: 14
Упражнение 1. 14
Упражнение 2. 14
Упражнение 3. 14
Упражнение 4. 15
Упражнение 5. 15
1.2. Алгебра высказываний. Основные законы математической логики. 15
Что есть высказывание. 15
Простые и составные высказывания. 16
Логические операции. 16
Порядок старшинства операций. 20
5. Основные законы математической логики. 21
6. Парадоксы логики (семантические парадоксы), или «правдоподобные» рассуждения, приводящие к противоречивым результатам. 21
7. Основная цель математической логики – обеспечить систему формальных обозначений для рассуждений, встречающихся не только в математике, но и в повседневной жизни. 21
Задачи для самостоятельного решения. 23
1.3. Числа. 24
2. Матрицы. Действия с матрицами. 25
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу). 26
3) Действие третье. Транспонирование матрицы.. 28
4) Действие четвертое. Сумма (разность) матриц. 29
5) Действие пятое. Умножение матриц. 30
6) Действие шестое. Нахождение обратной матрицы. 32
2.1. Вычисление определителей. 32
2.2. Вычисление обратной матрицы.. 37
2.3. Решение системы линейных уравнений. 42
Решение системы линейных уравнений методом подстановки. 43
Пример 1. 44
Пример 2. 45
Решить систему линейных уравнений с тремя неизвестными. 45
Пример 3. 47
Решить систему линейных уравнений с 4 неизвестными. 47
Решение системы методом почленного сложения (вычитания) уравнений системы.. 47
Пример 4. 47
Пример 5. 48
Пример 6. 50
Продолжение урока на странице Правило Крамера. Метод обратной матрицы >>>. 50
Решение системы по правилу Крамера. 50
Рассмотрим систему уравнений 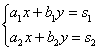 ........................ 51
........................ 51
Пример 7. 51
Ответ: 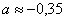 ,
, 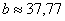 ............... 52
............... 52
Решение системы с помощью обратной матрицы.. 55
Пример 11. 55
Пример 12. 58
Ответы: 58
Пример 3: 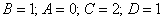 ........................................ 58
........................................ 58
Полное решение примеров 8, 10, 12 >>>. 58
Решение системы линейных уравнений методом Гаусса (последовательного исключения неизвестных) 58
Существуют следующие элементарные преобразования: 59
Элементарные преобразования не меняют решение системы уравнений. 61
Пример 1. 62
Теперь первая строка у нас останется неизменной до конца решения. Уже легче. 63
В третьем уравнении у нас уже готовый результат: 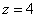 ........ 65
........ 65
Пример 2. 65
Пример 3. 66
Пример 4. 67
Пример 5. 68
Решения и ответы: 68
Несовместные системы. Системы с общим решением. Частные решения. 70
Пример 1. 71
Пример 2. 72
Пример 3. 72
Пример 4. 76
Пример 5. 76
Пример 6. 79
Решения и ответы: 80
Ответ: Общее решение: 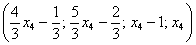 ................................................ 82
................................................ 82
3. Комплексные числа. 83
Не занимайтесь комплексными числами после комплексного обеда. 83
Понятие комплексного числа. 83
Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел. 86
Сложение комплексных чисел. 86
Пример 1. 86
Сложить два комплексных числа 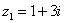 ,
, 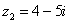 ................ 86
................ 86
Вычитание комплексных чисел. 86
Пример 2. 86
Умножение комплексных чисел. 87
Пример 3. 87
Найти произведение комплексных чисел 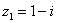 ,
, 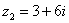 ................ 87
................ 87
Деление комплексных чисел. 87
Пример 4. 87
Пример 5. 88
Пример 6. 88
Тригонометрическая и показательная форма комплексного числа. 89
Модуль комплексного числа 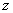 стандартно обозначают:
стандартно обозначают: 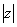 или
или 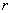 .. 90
.. 90
Аргумент комплексного числа 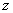 стандартно обозначают:
стандартно обозначают: 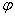 или
или 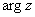 ........ 90
........ 90
Пример 7. 90
Таким образом, запись принимает вид: 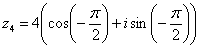 ................................................. 92
................................................. 92
Пример 8. 93
Число 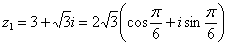 – так:
– так: 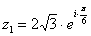 ...................... 95
...................... 95
Возведение комплексных чисел в степень. 96
Пример 9. 96
Возвести в квадрат комплексное число 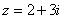 ............... 96
............... 96
Пример 10. 96
Пример 11. 97
Пример 12. 97
Возвести в степень комплексные числа 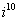 ,
, 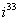 ,
, 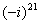 ......... 97
......... 97
Пример 13. 98
Возвести в степень комплексные числа 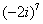 ,
, 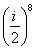 ........ 98
........ 98
Извлечение корней из комплексных чисел. 98
Пример 14. 98
Решить квадратное уравнение 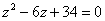 ......................... 98
......................... 98
Пример 15. 99
Как извлечь корень из произвольного комплексного числа?. 99
Пример 16. 99
Найти корни уравнения 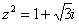 ................... 99
................... 99
Пример 17. 100
Найти корни уравнения 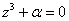 , где
, где 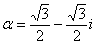 ....................... 100
....................... 100
По такому же алгоритму строится точка 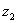 ... 102
... 102
Решения и ответы: 103
4. Математические формулы и графики. 104
Для того чтобы успешно решать задачи по высшей математике НЕОБХОДИМО: 104
Математические формулы и таблицы.. 107
Горячие формулы школьного курса математики. 107
Калькулятор для автоматических расчетов. 108
Тригонометрические формулы.. 108
Тригонометрические таблицы.. 108
Графики и свойства элементарных функций. 108
Графики и основные свойства элементарных функций. 108
Как правильно построить координатные оси?. 109
Любой чертеж графика функции начинается с координатных осей. 109
Трехмерный случай. 110
Графики и основные свойства элементарных функций. 111
График линейной функции. 111
Пример 1. 111
График квадратичной, кубической функции, график многочлена. 114
Пример 2. 115
Таким образом, вершина находится в точке 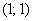 ....... 115
....... 115
Если 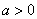 , то ветви параболы направлены вверх. 116
, то ветви параболы направлены вверх. 116
Если 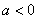 , то ветви параболы направлены вниз. 116
, то ветви параболы направлены вниз. 116
Кубическая парабола. 116
График функции 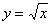 ............ 119
............ 119
График гиперболы.. 121
График функции вида 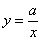 (
( 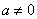 ) представляют собой две ветви гиперболы. 122
) представляют собой две ветви гиперболы. 122
Пример 3. 122
Построить правую ветвь гиперболы 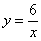 ......... 122
......... 122
График показательной функции. 123
График логарифмической функции. 125
Обязательно нужно знать и помнить типовое значение логарифма: 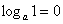 . 125
. 125
Графики тригонометрических функций. 126
Построим график функции 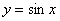 .............. 126
.............. 126
График косинуса. 127
Построим график функции 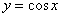 .............. 127
.............. 127
В отличие от синуса в косинусе минус «бесследно пропадает». 127
Графики тангенса и котангенса. 128
Построим график функции 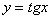 ............ 128
............ 128
Графики обратных тригонометрических функций. 130
Построим график арксинуса 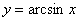 ................... 130
................... 130
Построим график арккосинуса 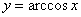 ................... 130
................... 130
Арктангенс – функция нечетная: 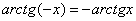 . 132
. 132
· Об авторах-составителях
Мелкумян Баграт Владимирович – кандидат физико-математических наук, доцент. Читает лекции и проводит семинарские занятия в Московском университете им. С. Ю. Витте по различным разделам дисциплины «Математика» на факультетах экономики и финансов, управления и юридическом. Преподает дисциплины «Базы данных», «Проектирование информационных систем», «Разработка и стандартизация программных средств и информационных технологий» и «Физика» на факультете управления для специальности «Прикладная информатика в экономике» различных форм обучения. Область научных интересов связана с разработкой лазерных устройств и использованием методов математической физики в системах управления.
Питерцева Галина Александровна – кандидат технических наук, доцент, почетный профессор Московского университета им. С. Ю. Витте. Область научных интересов связана с использованием математических методов в экономике РФ. В 2006 году была награждена знаком «Отличник высшего и профессионального образования». Читает лекции и проводит семинарские занятия по дисциплине «Математика» на факультетах экономики и финансов, управления, подготовительных курсах. Является автором курсов лекций и комплекса учебно-методических материалов по Математике для студентов и абитуриентов. Является разработчиком банков тестовых заданий по Математике для центра тестирования и для вступительных экзаменов.
· От авторов-составителей
Математика является точной абстрактной наукой, изучающей количественные соотношения и пространственные формы. Точность математики означает, что основным методом в математических исследованиях являются строгие логические рассуждения. В древности областями применения математики были: землемерие, счет, торговля, архитектура и астрономия. В XVII-XVIII вв. появилась «Высшая математика» с направлениями аналитической геометрии, векторной и матричной алгебры, дифференциального исчисления, интегрального исчисления, дифференциальных уравнений, и т. д. В XIX-ХХ вв. на основе математики развиваются новые дисциплины: теория информации, теория оптимального управления и математическое программирование. В XX-XXI вв., благодаря быстродействующим вычислительным машинам, в использовании математических методов произошел качественный скачок.
Математическое мышление неудержимо проникает в практику экономических и гуманитарных наук, и следует быть к этому готовым.
Эти лекции предназначены для слушателей гуманитарных специальностей, изучающих курс математики в соответствии с учебными программами Московского университета им. С. Ю. Витте. Лекции курса дополняются примерами решения задач и контрольными упражнениями, которые облегчают понимание, показывают пользу теории, а также ликвидируют общеизвестную боязнь перед математикой.
ВВОДНАЯ ЧАСТЬ
Наш курс не отвечает на вопрос: ЗАЧЕМ НУЖНА ВЫСШАЯ МАТЕМАТИКА? Действительно, большинству из вас она никогда не потребуется. Это факт. Но изучение высшей математики предусмотрено учебными планами практически всех ВУЗов, и появляются задания, контрольные работы, которые необходимо сдавать. Тоже факт. Предлагаемый курс отвечает на вопрос: КАК ЭТО РЕШАТЬ?
Лекции носят сугубо практическую направленность, и при изучении той или иной темы мы даже не всегда вам расскажем, ЧТО ЭТО ТАКОЕ и не всегда дадим строгие математические определения.
Но на глобальный вопрос ответим. Один раз. Так ЗАЧЕМ ЖЕ НУЖНА ВЫСШАЯ МАТЕМАТИКА? Изучение высшей математики очень хорошо развивает интеллект, как «фитнес для ума». Если Вы освоили высшую математику, то сможете разобраться в любом предмете, в любой профессиональной деятельности. А может, и станете олигархом, или председателем кабинета министров, как Сергей Юльевич Витте, который имел математическое высшее образование.
Нужны ли способности?
Способности человека всегда можно распознать по одному надежному правилу: человеку интересно то, к чему он имеет способности. Нельзя отрицать, что в математике (как и во всех областях труда, науки и искусства) существует нечто непостижимое, что называется талантом. Но опыт показывает, что крупица таланта есть у каждого. Для изучения же математики не требуется никаких особых способностей, например поразительной памяти, главное - это интерес, его нужно поддержать.
Что такое абстракция?
Конкретные вещи мы видим, осязаем. Абстрактные понятия (например, свобода) требуют соответствующего определения. Нужно знать и понимать определения математических абстрактных понятий.
Попробуем разобраться, что же такое абстракция в математике. Например, само вычисление есть уже определенный вид абстракции, обычный для мышления примитивных людей, хотя они не отдают себе в этом отчета. Пастух, пересчитывающий стадо, заботится только о том, сколько овец в наличии. Ему безразлично, каковы овцы - молодые или старые, белые или черные, действует принцип «штука, как штука».
Именно в этом существо абстракции: обращаем внимание только на некоторые особенности наблюдаемых предметов, отвлекаясь (абстрагируясь) от остальных. Математика безучастна к особенным свойствам предметов и изучает только их пространственные формы (геометрия) и количественные соотношения (анализ), т.е. то, что неизменно в самых различных областях. При изучении математических объектов обнаруживается родство между явлениями, на первый взгляд, совершенно различными.
План изучения курса
| № раздела/темы | Наименование разделов и тем (I семестр) | ||
| 01. | ВВОДНАЯ ЧАСТЬ | ||
| 1. | РАЗДЕЛ I. Алгебра высказываний | ||
| 1.1. | Аксиоматический метод и его понятийный аппарат | ||
| 1.2. | Основные законы математической логики | ||
| 2. | РАЗДЕЛ II. Алгебра матриц | ||
| 2.1. | Вычисление определителей | ||
| 2.2. | Вычисление обратной матрицы | ||
| 2.3. | Решение системы линейных уравнений | ||
| 3. | РАЗДЕЛ III. Алгебра комплексных чисел | ||
| 3.1. | Понятие комплексного числа | ||
| 3.2. | Алгебраическая форма комплексного числа | ||
| 3.3. | Тригонометрическая форма комплексного числа | ||
| 3.4. | Возведение комплексных чисел в степень | ||
| 3.5. | Извлечение корней из комплексных чисел | ||
| 4. | РАЗДЕЛ IV. Математические формулы и графики | ||
| 4.1. | Математические формулы и таблицы | ||
| 4.2. | Графики и свойства элементарных функций | ||
| 4.3. | Построение графиков функций. | К.р. №2 | |
| № раздела/темы | Наименование разделов и тем (II семестр) | Задание по теме | Срок сдачи работы |
| 5. | РАЗДЕЛ V. Пределы функций | ||
| 5.1. | Вычисление пределов | К.р. №3 | |
| 5.2. | Первый замечательный предел | К.р. №4 | |
| 5.3. | Второй замечательный предел | ||
| 6. | РАЗДЕЛ VI. Производная и дифференциал | ||
| 6.1. | Вычисление производных | ||
| 6.2. | Производная сложной функции | ||
| 6.3. | Логарифмическая производная и производная степенно-показательной функции | ||
| 6.4. | Производная функции, заданной неявно | ||
| 6.5. | Частные производные | ||
| 6.6. | Абсолютная и относительная погрешности вычислений | ||
| 6.7. | Приближённые вычисления с помощью дифференциалов функций одной и двух переменных | ||
| 7. | РАЗДЕЛ VII. Интегралы. | ||
| 7.1. | Неопределённый интеграл | ||
| 7.2. | Определённый интеграл | ||
| 7.3. | Несобственные интегралы | ||
| 7.4. | Эффективные методы вычисления определенных и несобственных интегралов | ||
| 7.5. | Приближенные формулы трапеций и метод Симпсона | ||
| 8. | РАЗДЕЛ VIII. Элементы теории вероятностей | ||
| 8.1. | Основные понятия теории множеств | ||
| 8.2. | Структуры на множестве. Элементы комбинаторики. | ||
| 8.3. | Случайные события и их вероятности. | ||
| 8.4. | Случайные величины и их характеристики. | ||
| 8.5. | Законы больших чисел | ||
| 8.6. | Применение теории вероятности в статистике |
График прохождения контрольных мероприятий:
| Недели прохождения контрольных этапов и сдачи заданий | |||||||||||||||||
| Вид работы | |||||||||||||||||
| КР |
Все контрольные работы выполняются полностью. Для самоконтроля даются ответы. Контрольные работы должны быть представлены в электронном виде.
ЛИТЕРАТУРА
Основной список
1. Красс М. С., Чупрынов Б. П. «Математика для экономистов». – СПб., 2007.
Дополнительный список
2. Общий курс высшей математики под ред. Ермакова. - М., 2004.
3. Кремер Н.Ш. «Математика». - М., 2003.
4. Шипачев В.С. «Высшая математика». - М., 2003.
5. Шипачев В.С. «Высшая математика». Задачник. - М., 2003.
6. http://mathprofi.ru/matematicheskie_formuly.html
Алгебра высказываний
Определение.
В любой науке, в математике тоже, существуют некоторые понятия, которые мы принимаем за исходные, или начальные понятия. Это так называемые основные понятия, определить которые достаточно сложно (именно потому, что они основные) и содержание которых можно выяснить только из опыта. Таковы, например, понятия: точки в геометрии, прямой в планиметрии, плоскости в стереометрии, материи в физике, информации в информатике.
Все остальные понятия мы объясняем, выражая их через начальные понятия. Такие объяснения называются определениями. Таким образом, каждое математическое определение опирается либо непосредственно на начальные понятия, либо на понятия, определённые прежде.
Однако здесь невозможно обеспечить всеобщего согласия. Дело в том, что одно и то же, например, геометрическое понятие можно определять различно. Диаметр окружности, например, можно определить как хорду, проходящую через центр, или как хорду наибольшей длины. Приняв за определение одно из этих свойств, можно доказать другое. Отметим, что обычно за определение берут простейшее свойство.
Доказательство. Теорема.
Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством.
Высказывание, которое можно доказать, называется теоремой. Как было указано выше, опыт проверяет истинность аксиом в их совокупности. Проверка состоит в том, что все теоремы математики оказываются согласными с опытом. Этого не случилось бы, если бы система аксиом была ложной.
Каждая теорема может быть выражена в формализованной математической форме вида:
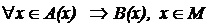
(читается: «для любого элемента х из А(х) следует В(х), где х принадлежит множеству М»).
Посылка А называется условием теоремы, а следствие В – заключением. Теорема верна, если выражающая её логическая связка, в данном случае это импликация 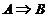 (читается: «из А следует В», или «если А, то В»), обеспечивает истинное высказывание.
(читается: «из А следует В», или «если А, то В»), обеспечивает истинное высказывание.
Рассмотрим примеры:
Теорема 1. Если сумма цифр натурального числа делится на 3, то и само число делится на 3.
Теорема 2. Если четырёхугольник является прямоугольником, то его диагонали конгруэнтны.
Теорема 3. Диагонали ромба взаимно перпендикулярны.
Из-за краткости формулировки теоремы 3 о диагоналях ромба может показаться, что эта теорема не имеет формы 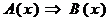 . На самом деле это не так. Полная формулировка этой теоремы такова (напомним, что ромбом называется параллелограмм, у которого все стороны равны): «Для любого параллелограмма верно утверждение: если параллелограмм – ромб, то его диагонали взаимно перпендикулярны».
. На самом деле это не так. Полная формулировка этой теоремы такова (напомним, что ромбом называется параллелограмм, у которого все стороны равны): «Для любого параллелограмма верно утверждение: если параллелограмм – ромб, то его диагонали взаимно перпендикулярны».
Упражнение 1.
Установите правильное соответствие между математическим утверждением и его формулировкой.
| 1. «В любой треугольник можно вписать окружность». | А. Определение B. Аксиома C. Теорема |
| 2. «Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник». | |
| 3. «Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна». |
Упражнение 2.
Выберите правильный ответ. К неопределяемым понятиям аксиоматического построения геометрии на плоскости относятся …
| 1) фигура, плоскость, луч | 2) луч, треугольник, плоскость |
| 3) точка, прямая, плоскость | 4) точка, отрезок, плоскость |
Упражнение 3.
Среди предложенных математических утверждений евклидовой геометрии аксиомой является…
1) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
2) Две прямые, параллельные третьей прямой, параллельны.
3) Две прямые на плоскости называются параллельными, если они не пересекаются.
4) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Упражнение 4.
Установите правильное соответствие между математическим утверждением и его формулировкой.
| 1. «Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны». | А. Определение B. Аксиома C. Теорема |
| 2. «На каждой прямой и в каждой плоскости имеются, по крайней мере, две точки». | |
| 3. «Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны». |
Упражнение 5.
Среди предложенных математических утверждений аксиомой является…
1) Через любые две точки плоскости можно провести прямую, и притом только одну.
2) В равнобедренном треугольнике углы при основании равны.
3) Диагонали параллелограмма точкой пересечения делятся пополам.
4) Вертикальные углы равны.
Что есть высказывание.
Под высказыванием понимают всякое утверждение, о котором имеет смысл говорить, что оно истинно или ложно.
Например, « 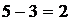 » или «В неделе семь дней» - истинные высказывания, а «
» или «В неделе семь дней» - истинные высказывания, а « 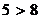 » или «В современном русском языке 35 букв» - ложные высказывания.
» или «В современном русском языке 35 букв» - ложные высказывания.
Высказывания могут быть образованы с помощью слов или символов. Синонимами слова «высказывание» считаются «логическое высказывание», «булевское выражение», «суждение» и «утверждение». Однако далеко не каждый набор слов или символов, даже, на первый взгляд, осмысленный, является математическим «высказыванием». Например, фразы: «Ура, у нас математика!» или «Который час?» или выражение « 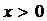 » высказываниями не являются, т.к. судить об их истинности или ложности невозможно.
» высказываниями не являются, т.к. судить об их истинности или ложности невозможно.
Таким образом, каждое математическое высказывание или истинно, или ложно; одновременно быть и истинным и ложным высказывание не может.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА», «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «0», «НЕТ», «Л», «-», «false»).
Для обозначения высказываний обычно используют заглавные буквы латинского алфавита A, B, C и т.д.
Например, пишут
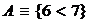 ,
, 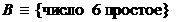 .
.
Это означает, что высказывание В заключается в утверждении, что число 6 – простое, а высказывание А – в том, что 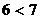 . Знак
. Знак 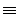 заменяет слова «есть высказывание», или «тождественно равно».
заменяет слова «есть высказывание», или «тождественно равно».
Логические операции
Операции над высказываниями – логические операции – обычно задают в виде таблиц, называемых таблицами истинности.
Операция отрицания, или отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 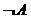 (читается «не А», или «не верно, что А») – это отрицание высказывания А. Высказывание
(читается «не А», или «не верно, что А») – это отрицание высказывания А. Высказывание 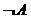 истинно, когда А – ложно, и ложно, когда А – истинно.
истинно, когда А – ложно, и ложно, когда А – истинно.
Таблица истинности для операции отрицания:
| А | 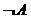 |
Отрицание – одноместная, или унарная, операция.
Последующие операции – двухместные, или бинарные.
Например, если 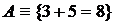 - истинное высказывание, то
- истинное высказывание, то
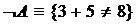 - ложное высказывание (отрицание А).
- ложное высказывание (отрицание А).
Отметим, что если 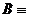 {в комнате холодно}, то
{в комнате холодно}, то 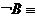 {в комнате не холодно}, но при этом высказывание
{в комнате не холодно}, но при этом высказывание 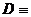 {в комнате жарко} отрицанием В не является.
{в комнате жарко} отрицанием В не является.
Операция конъюнкции, или конъюнкция высказываний.
Высказывание С, составленное из двух высказываний А и В при помощи союза «и», называют конъюнкцией (логическим произведением) этих высказываний: 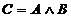 (выражение
(выражение 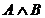 читается: «А и В»).
читается: «А и В»).
Логическое произведение 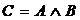 истинно только в том случае, когда и А, и В одновременно истинны.
истинно только в том случае, когда и А, и В одновременно истинны.
Таблица истинности для операции конъюнкции:
| А | В | 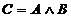 |
Пусть, например,  ,
,  . Тогда высказывание С – истинно, т. к. истинно каждое из высказываний А и В, составляющих высказывание С.
. Тогда высказывание С – истинно, т. к. истинно каждое из высказываний А и В, составляющих высказывание С.
Операцию конъюнкции можно определить и для нескольких высказываний, как связку высказываний, объединённых союзом «и». Конъюнкция из n высказываний – новое высказывание, причём высказывание
А = 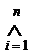 Аi ; где i = 1; 2; …; n
Аi ; где i = 1; 2; …; n
имеет значение «истина», если и А1, и А2, и … Аn одновременно истинны. Во всех других случаях эта конъюнкция имеет значение «ложь».
Пусть, например, А1 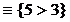 , А2
, А2 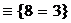 , А3
, А3  , А4
, А4 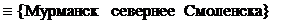 . Тогда высказывание
. Тогда высказывание
А2 Ù А3 Ù А4 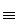 {(8 = 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – ложное, в то время как высказывание
{(8 = 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – ложное, в то время как высказывание
А1 Ù А3 Ù А4 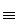 {(5 > 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – истинное.
{(5 > 3) и (отец старше сына) и (Мурманск севернее Смоленска)} – истинное.
Операция дизъюнкции, или дизъюнкция высказываний.
Высказывание С, составленное из двух высказываний А, В при помощи союза «или», называют дизъюнкцией (логической суммой) этих высказываний: 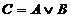 (выражение
(выражение 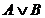 читается: «А или В»).
читается: «А или В»).
Сумма 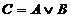 является истинным высказыванием тогда, когда, по крайней мере, одно из слагаемых истинно.
является истинным высказыванием тогда, когда, по крайней мере, одно из слагаемых истинно.
Таблица истинности для операции дизъюнкции:
| А | В | 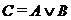 |
Пусть, например, 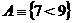 ,
, 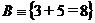 . Тогда высказывание
. Тогда высказывание 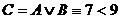 или
или 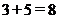 – истинно, т.к. истинно каждое из высказываний А и В, составляющих высказывание С.
– истинно, т.к. истинно каждое из высказываний А и В, составляющих высказывание С.
Операцию дизъюнкции можно определить и для нескольких высказываний как связку высказываний, объединённых союзом «или»:
А = 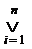 Аi ; где i = 1; 2; …; n
Аi ; где i = 1; 2; …; n
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Операция эквивалентности, или эквивалентность высказываний.
Высказывание С, составленное из двух высказываний А, В при помощи слов «тогда и только тогда, когда…», называют эквивалентностью высказываний А и В: 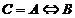 .
.
Для эквивалентности используют знак  (или ).
(или ).
Эквивалентность 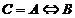 представляет собой истинное высказывание, когда высказывания и А, и В оба истинны или оба ложны.
представляет собой истинное высказывание, когда высказывания и А, и В оба истинны или оба ложны.
Таблица истинности для операции эквивалентности:
| А | В | 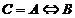 |
Пусть 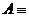 {число 3n является чётным},
{число 3n является чётным}, 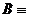 {число n является чётным}.
{число n является чётным}.
Высказывание 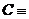 {число 3n является чётным тогда и только тогда, когда n – чётное число} есть эквивалентность высказываний А и В:
{число 3n является чётным тогда и только тогда, когда n – чётное число} есть эквивалентность высказываний А и В: 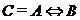 .
.
Операция импликации, или импликация высказываний.
Высказывание С, составленное из двух высказываний А, В при помощи слов «если…, то…», называют импликацией высказываний А и В: 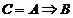 (выражение
(выражение 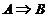 читается «из А следует В», или «если А, то В»).
читается «из А следует В», или «если А, то В»).
Импликация 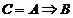 ложна только в том случае, когда А – истинное высказывание, а В – ложное. Во всех других случаях импликация имеет значение «истина».
ложна только в том случае, когда А – истинное высказывание, а В – ложное. Во всех других случаях импликация имеет значение «истина».
Таблица истинности для операции импликации:
| А | В | 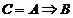 |
Первый член импликации 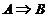 – высказывание А – называется посылкой, или условием, второй член В – заключением.
– высказывание А – называется посылкой, или условием, второй член В – заключением.
Обратите внимание, что таблица истинности для импликации, в отличии от таблиц для конъюнкции, дизъюнкции и эквивалентности, изменяется при перестановке столбцов для А и В.
Отметим также, что импликация не полностью соответствует обычному пониманию слов «если…, то…» и «следует». Из третьей и четвёртой строк таблицы истинности для импликации вытекает, что если А – ложно, то, каково бы ни было В, высказывание 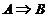 считается истинным. Таким о
считается истинным. Таким о
