Системы массового обслуживания.

Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания какого-либо потока заявок.

Примерами систем массового обслуживания могут служить:

· персональные компьютеры, обслуживающие поступающие заявки или требования на решение тех или иных задач;

· станции технического обслуживания автомобилей;

· аудиторские фирмы и т.д.

В CMО обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки на базах и складах.

Предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования.

Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания.

Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.

Классификация СМО:

По характеру случайного процесса, происходящего в СМО, различают системы Марковские и не Марковские.

Случайный процесс называется Марковским, если для любого момента времени t вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t и не зависят от того, когда и как система пришла в это состояние. Переходы системы из состояния в состояние происходят под действием каких-то потоков событий (поток заявок, поток отказов).

В случае не Марковских процессов задачи исследования СМО значительно усложняются и требуют применения статистического моделирования, численных методов с использованием ЭВМ.

По составу СМО бывают одноканальные (с одним обслуживающим устройством) и многоканальными (с большим числом обслуживающих устройств).

Элементы теории графов.

Теория графов – это раздел дискретной математики, изучающий свойства графов.

Граф – это пара множеств 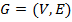, где V – это подмножество любого счётного множества, а E – подмножество V*V.

Маршрутом в графе называется конечная последовательность 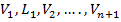, где 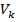– это вершины, 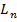– это ребра, причём ребро 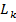соединяет вершины .

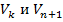Граф называется связным, если любые два элемента можно соединить маршрутом.

Маршрут, в котором первая и последняя вершина совпадают, а каждая из остальных встречается ровно один раз, называется циклом.

Связной граф без циклов называется деревом.

Сетевые модели.

Математический аппарат сетевых моделей базируется на теории графов.

Сеть – это ориентированный конечный связной граф, имеющий начальную и конечную вершину. Т.о., сетевая модель представляет собой граф вида «сеть».

Дерево представляет собой связный граф без циклов, имеющий исходную вершину и крайние вершины, а пути от исходной вершины к крайним называются ветвями.

В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управлениями СПЦ.

Основой сетевого планирования и управления является сетевая модель, в которой моделируется совокупность взаимосвязанных работ и событий, отображающий процесс достижения определённой цели. Она может быть представлена в виде графиков или таблицы.

Основные понятия сетевой модели:

1. событие

2. работа

3. путь

Событие – это результат выполнения одной или нескольких работ. Событие совершается в то момент, когда оканчивается последняя из работ, входящих в него.

Деревья. Остовные деревья

Дерево – это связный ациклический граф.

Дерево – это связный граф без цикла.

Любой граф без цикла называется ….Ребра дерева называются ветвями. Конечные вершины т.е. вершины степени 1называются листья.

Ориентированный граф называется ориентированным деревом если существует ровно одна вершина называемая корнем, которая не имеет предшествующих, и любой вершины несовпадающих с корнем предшествует равно одна вершина.

В произвольном графе G=(V,E) можно выделить подграф G,т.е. G^’=(V,E^’), E^’ с E, который является деревом это дерево называется стягивающим или оставным.

Ребра которые не вошли в дерево называются хордами.

Теорема. Число деревьев в связном графе равно алгебраическому дополнению любого элемента матрицы Кегрофа